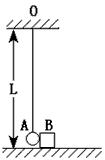
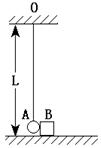
摘要：如图所示.长为L的细绳竖直悬挂着一质量为2m的小球A.恰好紧挨着放置在水平面上质量为m的物块B.现保持细绳绷直.把小球向左上方拉至细绳与竖直方向成60°的位置.然后释放小球.小球到达最低点时恰好与物块发生碰撞.而后小球向右摆动的最大高度为.物块则向右滑行了L的距离而静止.求物块与水平面间的动摩擦因数μ. 解析:设小球与物块碰撞前瞬间的速度为v0.对于其下摆的过程.由机械能守恒定律得: ·2m·v＝2mg(L-Lcos 60°) 解得:v0＝ 设碰撞后瞬间小球.物块的速度大小分别为v1.v2 由机械能守恒定律对于小球有: ·2m·v＝2mg· 由动量守恒定律有:2m·v0＝2m·v1+mv2 解得:v2＝ 对于物块向右滑行的过程.由动能定理有: μmgL＝mv 解得:μ＝0.5. 答案:0.5

网址：http://m.1010jiajiao.com/timu3_id_1374384[举报]