摘要： 图2-4-12 如图2-4-12所示.一根弹性细绳原长为l.劲度系数为k.将其一端穿过一个光滑小孔O(其在水平地面上的投影点为O′).系在一个质量为m的滑块A上.A放在水平地面上．小孔O离绳固定端的竖直距离为l.离水平地面高度为h(h<mg/k).滑块A与水平地面间的最大静摩擦力为正压力的μ倍．问: (1)当滑块与O′点距离为r时.弹性细绳对滑块A的拉力为多大? (2)滑块处于怎样的区域内时可以保持静止状态? 解析:(1)当滑块与O′点的距离为r时.弹性细绳的伸长量为Δx＝ . 由胡克定律知.弹性绳的拉力F＝kΔx＝k (2)设OA与水平面的夹角为α.分析物体受力如图所示.由平衡条件得: FN+Fsin α＝mg Fcos α＝Ff. 而F＝k.Ffm＝μFN 所以有:k·cos α＝Ff≤Ffm＝μ(mg-Fsin α)＝μ(mg-kh) 其中cos α＝r.故r≤ 答案:(1)k (2)以O′为圆心.以为半径的圆内的任何位置
网址：http://m.1010jiajiao.com/timu3_id_1374178[举报]
如图3－4－12所示，有五个力作用于一点P，构成一个正六边形的两个邻边和三条对角线，设F3=10N，则这五个力的合力大小为（ ）?
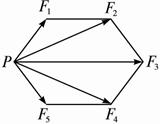
图3－4－12
? A．10（2+
）N? ? B．20 N??
C．30 N D．0?
查看习题详情和答案>>
如图3－4－12所示，有五个力作用于一点P，构成一个正六边形的两个邻边和三条对角线，设F3=10N，则这五个力的合力大小为（ ）?
图3－4－12
? A．10（2+
）N? ? B．20 N??
C．30 N D．0?
查看习题详情和答案>>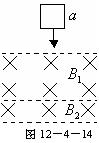
如图12－4－14所示，质量为m、边长为a的正方形金属线框自某一高度由静止下落，依次经过
和
两磁场区域．已知
，且磁场的高度为a．线框在进入的过程中做匀速运动，速度大小为
，在中加速一段时间后又匀速进入和穿出时速度恒为
，求：
（1）和之比
（2）在整个下落过程中线框中产生的焦耳热．
查看习题详情和答案>>
如图12－4－16所示，两根相距
的平行金属长导轨，固定在同一水平面内，并处于竖直方向的匀强磁场中，磁场的磁感应强度
．导轨上面横放着两根金属细杆，构成矩形回路，每根金属细杆的电阻
，回路中其余部分的电阻不计．已知两金属细杆在平行于导轨的拉力作用下，沿导轨朝相反方向匀速平移，速度大小都是
．不计导轨上的摩擦．
的滑动过程中共产生的热量．
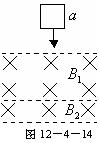如图12－4－14所示，质量为m、边长为a的正方形金属线框自某一高度由静止下落，依次经过
和
两磁场区域．已知
，且
，在
，求：