摘要:图示中滑块和小球的质量均为m.滑块可在水平放置的光滑固定导轨上自由滑动.小球与滑块上的悬点O由一不可伸长的轻绳相连.轻绳长为l.开始时.轻绳处于水平拉直状态.小球和滑块均静止.现将小球由静止释放.当小球到达最低点时.滑块刚好被一表面涂有黏性物质的固定挡板粘住.在极短的时间内速度减为零.小球继续向左摆动.当轻绳与竖直方向的夹角θ=60° 时小球达到最高点.求: (1)从滑块与挡板接触到速度刚好变为零的过程中.挡板阻力对滑块的冲量. (2)小球从释放到第一次到达最低点的过程中.绳的拉力对小球做功的大小.[2008年高考·全国理综卷Ⅰ] 解析:(1)解法一 设小球摆至最低点时.滑块和小球的速度大小分别为v1.v2.对于滑块和小球组成的系统.由机械能守恒定律得:mv+mv=mgl 同理.滑块被粘住后.对于小球向左摆动的过程.有: mv=mgl 解得:v1=v2= 对于滑块与挡板接触的过程.由动量定理得: I=0-mv1 挡板对滑块的冲量I=-m.负号表示方向向左. 解法二 设小球摆至最低点时.滑块和小球的速度大小分别为v1.v2.由动量守恒定律得: mv1-mv2=0 对于小球向左摆动的过程.由机械能守恒定律得: mv=mgl 解得:v1=v2= 对于滑块与挡板接触的过程.由动量定理有: I=0-mv1 解得挡板对滑块的冲量为: I=-m.负号表示方向向左. 解法三 设小球摆至最低点时.滑块和小球的速度大小分别为v1.v2.由机械能守恒定律得: mv+mv=mgl 又由动量守恒定律得: mv1+m(-v2)=0 解得:v1=v2= 对于滑块与挡板接触的过程.由动量定理得: I=0-mv1解得挡板对滑块的冲量为: I=-m.负号表示方向向左. 解法四 由全过程的能量转换和守恒关系可得(滑块在碰撞时损失的能量等于系统机械能的减少量.等于滑块碰前的动能): ΔE=mgl-mgl=mv2 解得滑块碰前的速度为:v= 对于滑块与挡板接触的过程.由动量定理得: I=0-mv 解得挡板对滑块的冲量为: I=-m.负号表示方向向左. (2)解法一 对小球下摆的过程.由动能定理得: mgl+W=mv 解得细绳对其做的功为: W=-mgl. 解法二 绳的张力对小球所做功的绝对值等于滑块在碰前的动能(或等于绳子的张力对滑块做的功).则有: W′=mv或W′=mv-0 解得:W=-W′=-mgl. 解法三 绳子的张力对小球做的功等于小球在全过程中的机械能的增量.取滑块所在高度的水平面为参考平面.有: W=(-mg·)-0=-mgl(取水平位置为重力势能零点) 或W=mgl-mgl=-mgl(取最低点为重力势能零点) 或W=0-mg·=-mgl(取小球运动到的最高点为重力势能零点). 解法四 对小球运动的全过程.由动能定理得: W+mglcos 60°=0或W+mg·=0 解得:W=-mgl. 解法五 考虑小球从水平位置到最低点的过程: 若滑块固定.绳子的张力对小球不做功.小球处于最低点时的速率v球′=(由mgl=mv球′2得到) 若滑块不固定.绳子的张力对小球做功.小球处于最低点时的速率v球=(v球应由前面正确求得) 则绳子对小球做的功为: W=mv-mv球′2=-mgl. 答案:(1)-m.负号表示方向向左 (2)-mgl
网址:http://m.1010jiajiao.com/timu3_id_1373944[举报]
如图9所示中滑块和小球的质量均为m,滑块可在水平放置的光滑固定导轨上自由滑动,小球与滑块上的悬点O由一不可伸长的轻绳相连,轻绳长为l。开始时,轻绳处于水平拉直状态,小球和滑块均静止。现将小球由静止释放,当小球到达最低点时,测得滑块对导轨的压力为3mg。求小球从释放到第一次到达最低点的过程中,绳的拉力对小球做功的大小。
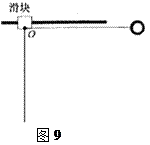
如图9所示中滑块和小球的质量均为m,滑块可在水平放置的光滑固定导轨上自由滑动,小球与滑块上的悬点O由一不可伸长的轻绳相连,轻绳长为l。开始时,轻绳处于水平拉直状态,小球和滑块均静止。现将小球由静止释放,当小球到达最低点时,测得滑块对导轨的压力为3mg。求小球从释放到第一次到达最低点的过程中,绳的拉力对小球做功的大小。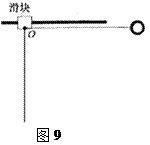

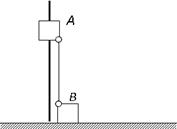
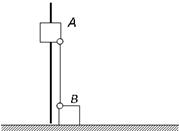 如图所示,滑块A、B的质量均为m,A套在固定竖直杆上,A、B通过转轴用长度为L的刚性轻杆连接,B放在水平面上并靠着竖直杆,A、B均静止.由于微小的扰动,B开始沿水平面向右运动.不计一切摩擦,滑块A、B视为质点.在A下滑的过程中,则下列说法中不正确的是(以水平面为零势能面)( )
如图所示,滑块A、B的质量均为m,A套在固定竖直杆上,A、B通过转轴用长度为L的刚性轻杆连接,B放在水平面上并靠着竖直杆,A、B均静止.由于微小的扰动,B开始沿水平面向右运动.不计一切摩擦,滑块A、B视为质点.在A下滑的过程中,则下列说法中不正确的是(以水平面为零势能面)( )| A、滑块A下滑到地面过程中两球和杆组成的系统机械能守恒 | ||
| B、滑块A下滑到地面过程中轻杆一直对B球做正功 | ||
C、滑块A着地时的速度为
| ||
D、滑块B机械能最大值为
|
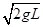
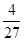 mgL
mgL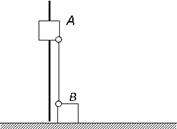
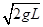
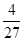 mgL
mgL