网址：http://m.1010jiajiao.com/timu3_id_1371061[举报]
某学习小组利用自行车的运动“探究阻力做功与速度变化的关系”．人骑自行车在平直的路面上运动,当人停止蹬车后,由于受到阻力作用,自行车的速度会逐渐减小至零,如图所示．在此过程中,阻力做功使自行车的速度发生变化．设自行车无动力后受到的阻力恒定．
(1)在实验中使自行车在平直的公路上获得某一速度后停止蹬车,需要测出人停止蹬车后自行车向前滑行的距离s,为了计算自行车的初速度v,还需要测量___________________________（填写物理量的名称及符号）．
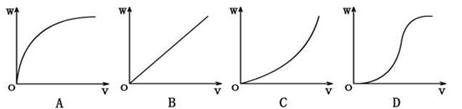
(2)设自行车受到的阻力恒为f,计算出阻力做的功W及自行车的初速度v．改变人停止蹬车时自行车的速度,重复实验,可以得到多组测量值．以阻力对自行车做功的大小为纵坐标,自行车初速度为横坐标,作出W-v曲线.分析这条曲线,就可以得到阻力做的功与自行车速度变化的定性关系．在实验中作出W-v图象如图所示,其中符合实际情况的是 ________．
查看习题详情和答案>>
某学习小组利用自行车的运动“探究阻力做功与速度变化的关系”．人骑自行车在平直的路面上运动,当人停止蹬车后,由于受到阻力作用,自行车的速度会逐渐减小至零,如图所示．在此过程中,阻力做功使自行车的速度发生变化．设自行车无动力后受到的阻力恒定．
(1)在实验中使自行车在平直的公路上获得某一速度后停止蹬车,需要测出人停止蹬车后自行车向前滑行的距离s,为了计算自行车的初速度v,还需要测量___________________________（填写物理量的名称及符号）．
(2)设自行车受到的阻力恒为f,计算出阻力做的功W及自行车的初速度v．改变人停止蹬车时自行车的速度,重复实验,可以得到多组测量值．以阻力对自行车做功的大小为纵坐标,自行车初速度为横坐标,作出W-v曲线.分析这条曲线,就可以得到阻力做的功与自行车速度变化的定性关系．在实验中作出W-v图象如图所示,其中符合实际情况的是 ________．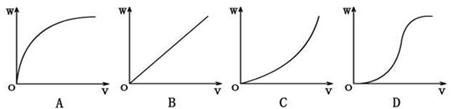
某学习小组利用自行车的运动“探究阻力做功与速度变化的关系”．人骑自行车在平直的路面上运动,当人停止蹬车后,由于受到阻力作用,自行车的速度会逐渐减小至零,如图所示．在此过程中,阻力做功使自行车的速度发生变化．设自行车无动力后受到的阻力恒定．
(1)在实验中使自行车在平直的公路上获得某一速度后停止蹬车,需要测出人停止蹬车后自行车向前滑行的距离s,为了计算自行车的初速度v,还需要测量___________________________（填写物理量的名称及符号）．
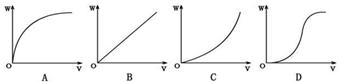
(2)设自行车受到的阻力恒为f,计算出阻力做的功W及自行车的初速度v．改变人停止蹬车时自行车的速度,重复实验,可以得到多组测量值．以阻力对自行车做功的大小为纵坐标,自行车初速度为横坐标,作出W-v曲线.分析这条曲线,就可以得到阻力做的功与自行车速度变化的定性关系．在实验中作出W-v图象如图所示,其中符合实际情况的是 ________．
某校物理兴趣小组举行了一场遥控赛车表演赛．赛车走过的路径如图所示．第一次表演，赛车从A点出发，以额定功率P=5W沿水平直轨道AB运动一段时间后关闭电源，再由B点进入半径为R的光滑竖直圆轨道，赛车恰好能通过竖直圆轨道最高点，然后沿圆轨道运动，进入另一条与AB轨道等高的光滑平直轨道，并从C点飞出．已知赛车质量m=lkg，可视为质点，进入竖直圆轨道前受到阻力大小恒定为f=0.3N．在运动中受到的其他阻力均可不计．g=10m/s2．已知A、B间距离L=10m，圆轨道半径R=0.18m，水平直轨道ABC与地面之间的高度差是h=1.8m，壕沟宽S=2.4m．C点在壕沟左边缘的正上方．求：（1）第一次表演时，赛车到达B点的速度多大？
（2）第二次表演，要使赛车越过壕沟，电动机至少要工作多长时间？
（2011?上海模拟）如图所示，沿水平方向放置一条平直光滑槽，它垂直穿过开有小孔的两平行薄板，板相距3.5L．槽内有两个质量均为m的小球A和B，A球带电量为+q，B球带电量为-3q，两球由长为2L的轻杆相连，组成一带电系统．最初A和B分别静止于左板的两侧，离板的距离均为L．若视小球为质点，不计轻杆的质量，现在两板之间加上与槽平行场强为E的向右的匀强电场后（设槽和轻杆由特殊绝缘材料制成，不影响电场的分布），带电系统开始运动．试求：（1）从开始运动到B球刚进入电场时，带电系统电势能的增量△ε；
（2）以右板电势为零，带电系统从运动到速度第一次为零时A球所在位置的电势UA为多大；
（3）带电系统从开始运动到速度第一次为零所需的时间．