摘要:必须区别开普勒第三行星定律中的常量K与万有引力定律中常量G的不同 (1)开普勒第三定律中的常量K: 开普勒第三定律中的常量K= r3/T2.对于行星与太阳的天体系统而言.常量K仅与太阳的质量有关而与行星的质量无关.此规律对于其它的由`中心天体’与`环绕天体’组成的天体系统同样适用.常量K仅由`中心天体’的质量决定而与`环绕天体’的质量无关.`中心天体’相同的天体系统中的常量K相同.`中心天体’不同的天体系统的常量K也不同.“K= r3/T2=常量 的伟大意义在于启发牛顿总结.发现了万有引力定律. (2)万有引力定律中的常量G: 万有引力定律中的常量G是由万有引力定律F=变形求出的.G=F r2/m1m2.数值是G=6.67×10-11Nm2/Kg2.是卡文迪许扭秤实验测出的.适用于宇宙间的所有物体.万有引力定律中的常量G的测定不仅证明了万有引力的存在.更体现了万有引力定律在天文研究中的巨大价值. (3)常量K与常量G的关系: 常量K与常量G有如下关系.K= GM/4π2.或者G=4π2/GM.K的值由`中心天体’的质量而定.而常量G则是一个与任何因素无关的普适常量. 例3:行星绕太阳运转的轨道是椭圆.这些椭圆在一般情况下可以近似视为圆周轨道.试用万有引力定律和向心力公式证明对所有绕太阳运转的行星.绕太阳公转轨道半径的立方与运转周期的平方的比值为常量.论述此常量的决定因素有哪些?此结论是否也适用于地球与月球的系统? [审题] 本题中行星绕太阳运转的轨道近似视为圆周轨道时.只要运用万有引力定律和向心力公式即可证明得出结论. [解析] 因为行星绕太阳运转需要的向心力是由太阳的万有引力提供.设太阳质量为M.行星的质量为m.行星绕太阳运转轨道的半径为r.运行周期为T.则. GMm/r2=m4π2r/T2,故.r3/T2=GM/4π2.即.K= GM/4π2. 显然.由于太阳质量一定.K的数值仅由太阳质量M决定.与其它因素无关.这一结论适用于地球与月球系统.也适用于其它`中心天体’与`环绕天体’组成的天体系统. [总结]开普勒第三定律中的常量K与万有引力定律中的常量G的这种关系(K= GM/4π2.或者G=4π2/GM)可以用来方便的求解卫星类的问题.作为一种解题的`切入口’应在解题过程中予以重视.
网址:http://m.1010jiajiao.com/timu3_id_1364752[举报]
下列说法正确的是
A.宇航员太空行走时,与飞船之间连有一根细绳,这样使宇航员处于平衡状态
B.在探究太阳对行星的引力规律时,我们引用了公式 ,这个关系式是开普勒第三定律,是可以在实验室中得到验证的
,这个关系式是开普勒第三定律,是可以在实验室中得到验证的
C.引力常量G是由实验测量得到,而不是理论推导出的
D.所有地球同步卫星所受的万有引力大小都相同
查看习题详情和答案>>
下列说法正确的是
| A.宇航员太空行走时,与飞船之间连有一根细绳,这样使宇航员处于平衡状态 |
B.在探究太阳对行星的引力规律时,我们引用了公式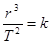 ,这个关系式是开普勒第三定律,是可以在实验室中得到验证的 ,这个关系式是开普勒第三定律,是可以在实验室中得到验证的 |
| C.引力常量G是由实验测量得到,而不是理论推导出的 |
| D.所有地球同步卫星所受的万有引力大小都相同 |