摘要： (1)塑胶炸药爆炸瞬间取A和B为研究对象.假设爆炸后瞬间AB的速度大小分别为vA.vB.取向右为正方向 由动量守恒:-mAvA+mBmB=0 ----- 爆炸产生的热量由9J转化为AB的动能: --- 带入数据解得:vA = vB =3m/s ------ 由于A在炸药爆炸后再次追上B的时候弹簧恰好第一次恢复到原长.则在A追上B之前弹簧已经有一次被压缩到最短.爆炸后取BC和弹簧为研究系统.当弹簧第一次被压缩到最短时BC达到共速vBC.此时弹簧的弹性势能最大.设为Ep1. 由动量守恒:mBvB=(mB+mC)vBC ------ 由能量定恒定定律: ------ 带入数据得:EP1 = 3 J ------ (2)设BC之间的弹簧第一次恢复到原长时B.C的速度大小分别为vB1和vC1.则由动量守恒和能量守恒: mBvB=mBvB1+mCvC1 ------ ------ 带入数据解得:vB1=-1m/s vC1=2m/s ------ (vB1 = 3 m/s vC1= 0 m/s 不合题意.舍去.) A爆炸后先向左匀速运动.与弹性挡板碰撞以后速度大小不变.反向弹回.当A追上B.发生碰撞瞬间达到共速vAB 由动量守恒:mAvA+mBvB1=(mA+mB)vAB ------ 解得:vAB = 1 m/s ------ 当ABC三者达到共同速度vABC时.弹簧的弹性势能最大为EP2 由动量守恒:(mA+mB)vAB+mCvC1=(mA+mB+mC)vABC ------ 由能量守恒: ---- 代入数据得:EP2 = 0.5 J ------ 点评:本题是通过弹簧.运用了能量观点.动量守恒的综合题.解决本题关键是运用运动守恒方程.能量观点方程求出速度的值再根据实际情况舍去不合题意的. 备用题18.如图所示.质量为M的长板静置在光滑的水平面上.左侧固定一劲度系数为K且足够长的水平轻质弹簧.右侧用一根不可伸长的细绳连接于墙上.细绳所能承受的最大拉力为T.让一质量为m.初速为v0的小滑块在长板上无摩擦地对准弹簧水平向左运动(已知弹簧的弹性势能为EP=.式中的是弹簧长度的变化量).试求: ⑴在什么情况下细绳会被拉断? ⑵细绳被拉断后.长板所能获得的最大加速度多大? ⑶滑块最后离开长板时.相对地面速度恰为零的条件是什么?
网址：http://m.1010jiajiao.com/timu3_id_1362442[举报]
(16分)(1)某同学在做“利用单摆测重力加速度”的实验中，先测得摆线长为97.50cm；再用20分度的游标卡尺(测量值可准确到0.05mm)测得摆球直径的读数如图所示。则摆球直径为________cm；然后用秒表记录了单摆振动50次所用的时间为99.9s。则
①该摆摆长为_______cm，(摆长准确到0.01cm)
周期为________s。
②如果他测得的重力加速度的值偏小，可能的原因是________。
A.测摆线长时摆线拉得过紧
B.摆线上端未牢固地系于悬点，振动中出现松动，使摆线长度增加了
C.开始计时，秒表过迟按下
D.实验中误将49次全振动数为50次
(2)为了提高测量精度,需多次改变摆长L的值并测得相应的周期T的值。现测得的六组数据标示在以L为横坐标、T2为纵坐标的坐标纸上,即图中用“
”表示的点。根据图中的数据点作出T2与L的关系图线，并通过图线求得的重力加速度g=________m/s2。
、
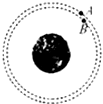“天宫一号”（Tiangong-1）是中国第一个目标飞行器，于2011年9月29日21时16分3秒在酒泉卫星发射中心发射，2011年11月3日凌晨顺利实现与“神州八号”飞船的对接任务．某同学画出“天宫一号”和“神舟八号”绕地球做匀速圆周运动的情景图，如图所示，A代表“天宫一号”，B代表“神舟八号”，虚线为各自的轨道，由图可以判定（ ）
查看习题详情和答案>>
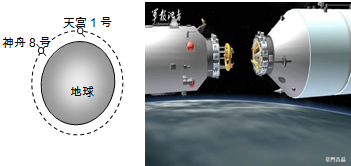2011年9月29日晚21时16分，我国首个目标飞行器“天宫一号”发射升空，它进入工作轨道运行周期约为91min．在未来的两年内它将分别与“神舟八号”、“神舟九号”、“神舟十号”飞船对接，从而建立我国第一个空间实验室．右图是2011年11月3日“神舟8号”与“天宫一号”第一次“接吻”的情境．则下列说法中不正确的是（ ）