摘要:简谐运动 (1).简谐运动的判定 在简谐运动中.回复力的特点是大小和位移成正比.方向与位移的方向相反.即满足公式 F=-kx.所示对简谐运动的判定.首先要正确分析出回复力的来源.再根据简谐运动中回复力的特点进行判定. (2).简谐运动的特点 周期性:简谐运动的物体经过一个周期或n个周期后.能回复到原来的运动状态.因此处理实际问题时.要注意多解的可能性或需定出结果的通式.千万不要用特解代替通解. [例5]如图所示.质量为m的木块放在弹簧上.与弹簧一起在竖直方向上做简谐运动.当振幅为A时.物体对弹簧的最大压力是物体重力的1.5倍.则物体对弹簧的最小弹力是多大?要使物体在振动中不离开弹簧.振幅不能超过多大? 解析:当木块运动到最低点时.对弹簧弹力最大.此时由牛顿第二定律得: Fmax-mg=ma.因为Fmax=1.5mg.所以a=0.5g. 当木块运动到最高点时.对弹簧弹力最小.此时由牛顿第二定律得: mg-Fmin=ma.由运动的对称性知.最高点与最低点的加速度大小相等.即 a=0.5g.代入求得Fmin=mg/2. 在最高点或最低点:kA=ma=.所以弹簧的劲度系数k=. 物体在平衡位置下方处于超重状态.不可能离开弹簧.只有在平衡位置上方可能离开弹簧.要使物体在振动过程中恰好不离开弹簧.物体在最高点的加速度a=g此时弹簧的弹力为零.若振幅再大.物体便会脱离弹簧.物体在最高点刚好不离开弹簧时.回复力为重力.所以:mg=KA/.则振幅A/==2A. [例6]轻质弹簧上端固定在天花板上.下端悬挂物体m.弹簧的劲度系数为k.现将物体从平衡位置向下拉开一段距离后释放.试证明物体的运动是简谐振动. 解析:如图所示.设振子的平衡位置为O.向下方向为正方向.此时弹簧的形变为 .根据胡克定律及平衡条件有 ① 当振子向下偏离平衡位置为时.回复力为 ② 将①代人②得: . 可见.重物振动时的受力符合简谐运动的条件. [例7]一弹簧振子做简谐运动.周期为T.下述正确的是 A.若t时刻和(t+△t)时刻振子对平衡位置的位移大小相等.方向相同.则△t一定等于T的整数倍 B.若t时刻和(t+△t)时刻振子运动速度大小相等.方向相反.则△t一定等于的整数倍. C.若△t=.则在t时刻和(t+△t)时刻的时间内振子的位移可能大于振幅.可能等于振幅.可能小于振幅 D.若△t=.则在t时刻和(t+△t)时刻振子的速度大小一定相等
网址:http://m.1010jiajiao.com/timu3_id_1356600[举报]
 一列简谐横波在某时刻的波形如图所示,此时刻质点P的速度为v,经过0.2s它的速度大小、方向第一次与v相同,再经过1.0s它的速度大小、方向第二次与v相同,则下列判断中正确的有( )
一列简谐横波在某时刻的波形如图所示,此时刻质点P的速度为v,经过0.2s它的速度大小、方向第一次与v相同,再经过1.0s它的速度大小、方向第二次与v相同,则下列判断中正确的有( )
查看习题详情和答案>>
一列简谐横波在某时刻的波形如图所示,此时刻质点P的速度为v,经过0.2 s它的速度大小、方向第一次与v相同,再经过1.0 s它的速度大小、方向第二次与v相同,则下列判断中正确的有( )
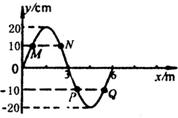
A.波沿x轴的正方向传播,波速为5 m/s
B.质点M与质点Q的位移大小总是相等、方向总是相反
C.若某时刻质点M到达波谷处,则质点P一定到达波峰处
D.从图示位置开始计时,在1.2 s时刻,质点P运动的路程为80cm
查看习题详情和答案>>有一列简谐波沿x轴正方向传播.在x轴上每相隔1m依次有A、B、C、D、E、F、G、H、I等9个质点.A是波源.开始t =0时刻观察到质点A在x轴上刚向上运动,在 t =0.1s质点A第一次到达正向最大位移处,此时质点C刚开始在x轴上向上运动,由此可以判定
[ ]
A.这列波的波长为8m,周期为0.2s
B.这列波的波速为20m/s,频率为2.5Hz
C.质点 I 第一次到达正向最大位移处在0.50s时刻
D.质点 I 第一次到达正向最大位移处在0.45s时刻
查看习题详情和答案>>