图5-9-8

若按实验要求正确地选出纸带进行测量，量得连续三点A、B、C到第一个点的距离如图5-9-8所示（相邻计数点时间间隔为0.02 s）.那么：

（1）纸带的________端与重物相连；

（2）打点计时器打下计数点B时，物体的速度v_B=________;

（3）从起点O到打下计数点B的过程中重力势能减少量是ΔE_p=________，此过程中物体动能的增加量ΔE_k=________（取g=9.8 m/s²）;

（4）通过计算，数值上ΔE_p________ΔE_k（填“＞”“=”或“＜”），这是因为_____________；

（5）实验的结论是______________________________________________________.

在“验证机械能守恒定律”的实验中，所用电源的频率为50Hz，某同学选择了一条理想的纸带，用刻度尺测量时各计数点对应刻度尺上的读数如图所示，数值的单位是mm；图中O点是打点计时器打出的第一个点，A、B、C、D、E分别是每打两个点取出的计数点．设重物的质量为1kg，当地重力加速度g=9.8m/s²．( 结果均取3位有效数字)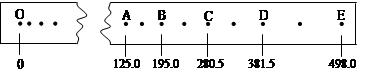

（1）重物从开始下落到计时器打B点时，减少的重力势能△E_P减           =_____________J；
（2）当计时器打B点时，重物的速度v_B=___________m/s；
（3）若求得重物下落到计时器打B点时增加的动能△E_k增 ，发现△E_P减       和△E_k增         并不严格相等，则产生误差的主要原因是_____________________________________．

在“验证机械能守恒定律”的实验中，所用电源的频率为50Hz，某同学选择了一条理想的纸带，用刻度尺测量时各计数点对应刻度尺上的读数如图所示，数值的单位是mm；图中O点是打点计时器打出的第一个点，A、B、C、D、E分别是每打两个点取出的计数点．设重物的质量为1kg，当地重力加速度g=9.8m/s²．( 结果均取3位有效数字)

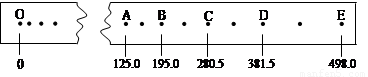
（1）重物从开始下落到计时器打B点时，减少的重力势能△E_P减           =_____________J；

（2）当计时器打B点时，重物的速度v_B=___________m/s；

（3）若求得重物下落到计时器打B点时增加的动能△E_k增 ，发现△E_P减       和△E_k增         并不严格相等，则产生误差的主要原因是_____________________________________．

在“验证机械能守恒定律”的实验中，所用电源的频率为50Hz，某同学选择了一条理想的纸带，用刻度尺测量时各计数点对应刻度尺上的读数如下图所示，数值的单位是mm，图中O点是打点计时器打出的第一个点，A、B、C、D、E分别是每打两个点取出的计数点，设重物的质量为m，当地重力加速度g=9.8m/s²。( 答案的数值或表达式的系数均取2位小数)

（1）重物从开始下落到计时器打B点时，减少的重力势能△E_P减            =_____________J。

（2）当计时器打B点时，重物的速度v_B=___________m/s。

（3）重物下落到计时器打B点时增加的动能△E_k增    =___________J。

（4）我们发现，△E_P减        和△E_k增          并不严格相等，产生误差的主要原因是__________________

_________________________________________________________________。