摘要:9.(1)当a=2m/s2竖直向下时.由牛顿第二定律.有F上+rng-F下=ma m=0.5kg. 当匣子顶部板压力传感器的示数是底部传感器的示数的一半时. F上=F下=5N 由牛顿第二定律.对m有F上+mg-2F下 =ma′ a′=0 所以升降机应作匀速运动 (2)若F上=0,则F下≥10N,设升降机的加速度为a1.则:F上-mg=ma1 a1=(F下-mg)/m=/0.5=10m/s2. 故升降机作向上的匀加速或向下的匀蛾逮运动.加速度a≥10m/s2. 10解析:设物体A从距B的高度H处自由落下.A与B碰撞前的速度为v1.由机械能守恒定律得 v1=. 设A.B碰撞后共同速度为v2.则由动量守恒定律得:Mv1=2Mv2. 解得: v2=. 当C刚好离开地面时.由胡克定律得弹簧伸长量为x=Mg/k.由于对称性.所以弹簧的弹性势能仍为E.当弹簧恢复原长时A.B分离.设此时A.B的速度为v3.则对A.B一起运动的过程中.由机械能守恒得: . 从A.B分离后到物体C刚好离开地面的过程中.物体B和弹簧组成的系统机械能守恒.即 . 联立以上方程解得:. 11解:先取A.B和弹簧整体为研究对象.弹簧弹力为内力.杆对A.B支持力与加速度方向垂直.在沿F方向应用牛顿第二定律 F=(mA+mB)a ①2分 再取B为研究对象.在沿F方向应用牛顿第二定律 ② 2分 联立①②求解得N 由几何关系得弹簧的伸长量 2分 弹簧的劲度系数 2分 代入数据解得k=100N/m 12解:(1)设两滑块碰前A的速度为v1.由动能定理有 解得:v1=3m/s A.B两滑块碰撞.由于时间极短动量守恒.设共同速度为v 解得:v=1.0m/s (2)碰后A.B一起压缩弹簧至最短.设弹簧压缩量为x1.由动能定理有: 解得:x1=0.02m 设反弹后A.B滑行了x2距离后速度减为零.由动能定理得: 解得:x2≈0.05m 以后.因为qE>μ(M+m)g.滑块还会向左运动.但弹开的距离将逐渐变小.所以.最大距离为:S=x2+s-x1=0.05m+0.05m-0.02m= 0.08m 13解析:设直杆匀速转动时.弹簧伸长量为x.A.B两球受力分别如图所示.据牛顿第二 定律得: 对A球有:FT-F=mω2L------2分 对B球有:F= mω2(2L+x)---------2分 其中F=kx FT= mω2L(1+) ,x=-----2分 所以弹簧总长度为 L’=L+x=L--------2分 14(1)设发生第一次作用后小车的速度为v1.由动量守恒定律.有 (2)设发生第二次作用后小车的速度为v2.由动量守恒定律.有
网址:http://m.1010jiajiao.com/timu3_id_1355937[举报]
A、B两球在光滑水平面上沿同一直线上、同一方向运动,mA=1kg,mB=2kg,vA=6m/s,vB=2m/s.当A球追上B球并发生碰撞后,A、B两球速度的可能值是 [ ]
A.v′A=5m/s,v′B=2.5m/s
B.v′A=2m/s,v′B=4m/s
C.v′A=-4m/s,v′B=7m/s
D.v′A=7m/s,v′B=1.5m/s
查看习题详情和答案>>
A、B两球在光滑水平面上沿同一直线上、同一方向运动,mA=1kg,mB=2kg,vA=6m/s,vB=2m/s.当A球追上B球并发生碰撞后,A、B两球速度的可能值是 [ ]
A.v′A=5m/s,v′B=2.5m/s
B.v′A=2m/s,v′B=4m/s
C.v′A=-4m/s,v′B=7m/s
D.v′A=7m/s,v′B=1.5m/s
查看习题详情和答案>>
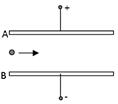
(10分)如图所示,质量为5×10-8kg的带电微粒以V0=2m/s的速度从水平放置的金属板A、B的中央飞入板间,已知板长L=10cm,板间距离d=2 cm.当UAB=1000V时,带电粒子恰好沿直线穿过板间,则
(1)UAB为多大时粒子擦上板边沿飞出?
(2)UAB在什么范围内带电粒子能从板间飞出?
查看习题详情和答案>>
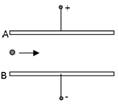
 0cm,板间距离d="2" cm.
0cm,板间距离d="2" cm. 当UAB=1000V时,带电粒子恰好沿直线穿过板间,则
当UAB=1000V时,带电粒子恰好沿直线穿过板间,则