摘要:23.如下图所示.在平面直角坐标系xOy中的第一象限内存在磁感应强度大小为B.方向垂直于坐标平面向内的有界圆形匀强磁场区域,在第二象限内存在沿x轴负方向的匀强电场.一粒子源固定在x轴上的A点.A点坐标为.粒子源沿y轴正方向释放出速度大小为v的电子.电子恰好能通过y轴上的C点.C点坐标为.电子经过磁场偏转后方向恰好垂直ON.ON是与x轴正方向成15°角的射线.(电子的质量为m.电荷量为e.不考虑粒子的重力和粒子之间的相互作用.)求: (1)第二象限内电场强度E的大小. (2)电子离开电场时的速度方向与y轴正方向的夹角θ. (3)圆形磁场的最小半径Rmin.
网址:http://m.1010jiajiao.com/timu3_id_1246574[举报]
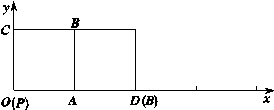
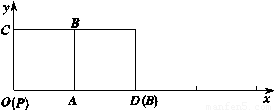
如图所示,在平面直角坐标系xOy中,正方形PABC的边长为1,将其沿x轴的正方向连续滚动,即先以顶点A为旋转中心将正方形PABC顺时针旋转90°得到第二个正方形,再以顶点D为旋转中心将第二个正方形顺时针旋转90°得到第三个正方形,依此方法继续滚动下去得到第四个正方形,…,第n个正方形.设滚动过程中的点P的坐标为(x,y).
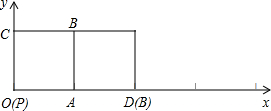
(1)画出第三个和第四个正方形的位置,并直接写出第三个正方形中的点P的坐标;
(2)画出点P(x,y)运动的曲线(0≤x≤4),并直接写出该曲线与x轴所围成区域的面积.
查看习题详情和答案>>

(1)画出第三个和第四个正方形的位置,并直接写出第三个正方形中的点P的坐标;
(2)画出点P(x,y)运动的曲线(0≤x≤4),并直接写出该曲线与x轴所围成区域的面积.
如图所示,在平面直角坐标系xOy中,正方形![]() 的边长为1,将其沿
的边长为1,将其沿![]() 轴的正方向连续滚动,即先以顶点A为旋转中心将正方形
轴的正方向连续滚动,即先以顶点A为旋转中心将正方形![]() 顺时针旋转90°得到第二个正方形,再以顶点D为旋转中心将第二个正方形顺时针旋转90°得到第三个正方形,依此方法继续滚动下去得到第四个正方形,…,第n个正方形.设滚动过程中的点P的坐标为
顺时针旋转90°得到第二个正方形,再以顶点D为旋转中心将第二个正方形顺时针旋转90°得到第三个正方形,依此方法继续滚动下去得到第四个正方形,…,第n个正方形.设滚动过程中的点P的坐标为![]() .
.
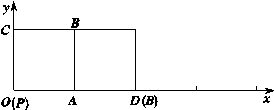
1.(1)画出第三个和第四个正方形的位置,并直接写出第三个正方形中的点P的坐标;
2.(2)画出点![]() 运动的曲线(0≤
运动的曲线(0≤![]() ≤4),并直接写出该曲线与
≤4),并直接写出该曲线与![]() 轴所围成区域的面积.
轴所围成区域的面积.
查看习题详情和答案>>
如图所示,在平面直角坐标系xOy中,正方形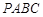 的边长为1,将其沿
的边长为1,将其沿 轴的正方向连续滚动,即先以顶点A为旋转中心将正方形
轴的正方向连续滚动,即先以顶点A为旋转中心将正方形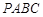 顺时针旋转90°得到第二个正方形,再以顶点D为旋转中心将第二个正方形顺时针旋转90°得到第三个正方形,依此方法继续滚动下去得到第四个正方形,…,第n个正方形.设滚动过程中的点P的坐标为
顺时针旋转90°得到第二个正方形,再以顶点D为旋转中心将第二个正方形顺时针旋转90°得到第三个正方形,依此方法继续滚动下去得到第四个正方形,…,第n个正方形.设滚动过程中的点P的坐标为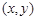 .
.
【小题1】(1)画出第三个和第四个正方形的位置,并直接写出第三个正方形中的点P的坐标;
【小题2】(2)画出点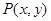 运动的曲线(0≤
运动的曲线(0≤ ≤4),并直接写出该曲线与
≤4),并直接写出该曲线与 轴所围成区域的面积.
查看习题详情和答案>>
轴所围成区域的面积.
查看习题详情和答案>>
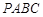 的边长为1,将其沿
的边长为1,将其沿 轴的正方向连续滚动,即先以顶点A为旋转中心将正方形
轴的正方向连续滚动,即先以顶点A为旋转中心将正方形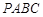 顺时针旋转90°得到第二个正方形,再以顶点D为旋转中心将第二个正方形顺时针旋转90°得到第三个正方形,依此方法继续滚动下去得到第四个正方形,…,第n个正方形.设滚动过程中的点P的坐标为
顺时针旋转90°得到第二个正方形,再以顶点D为旋转中心将第二个正方形顺时针旋转90°得到第三个正方形,依此方法继续滚动下去得到第四个正方形,…,第n个正方形.设滚动过程中的点P的坐标为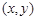 .
.
【小题1】(1)画出第三个和第四个正方形的位置,并直接写出第三个正方形中的点P的坐标;
【小题2】(2)画出点
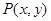 运动的曲线(0≤
运动的曲线(0≤ ≤4),并直接写出该曲线与
≤4),并直接写出该曲线与 轴所围成区域的面积.
查看习题详情和答案>>
轴所围成区域的面积.
查看习题详情和答案>>
 的边长为1,将其沿
的边长为1,将其沿 轴的正方向连续滚动,即先以顶点A为旋转中心将正方形
轴的正方向连续滚动,即先以顶点A为旋转中心将正方形 .
.
 运动的曲线(0≤
运动的曲线(0≤ 轴所围成区域的面积.
轴所围成区域的面积.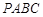 的边长为1,将其沿
的边长为1,将其沿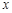 轴的正方向连续滚动,即先以顶点A为旋转中心将正方形
轴的正方向连续滚动,即先以顶点A为旋转中心将正方形 .
. 
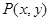 运动的曲线(0≤
运动的曲线(0≤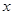 轴所围成区域的面积.
轴所围成区域的面积.