假期复习第六天―――函数的图象
一.这几个概念你掌握了吗?请回顾一遍:
1.熟练掌握基本函数的图象;
2.正确地从函数的图象特征去讨论函数的主要性质;
3.正确运用数形结合的思想方法解题.
4.三种图象变换:平移变换、对称变换和伸缩变换。
5.识图:分布范围、变化趋势、对称性、周期性等等方面.
二.特别要注意下列方法:
1.平移变换:(1)水平平移:函数 的图像
的图像
可以把函数 的图像沿
的图像沿 轴方向向左
轴方向向左 或
或
向右 平移
平移 个单位即可得到;
个单位即可得到;
(2)竖直平移:函数 的图像可以把函数
的图像可以把函数 的图像沿
的图像沿 轴方向向上
轴方向向上 或向下
或向下 平移
平移 个单位即可得到.
个单位即可得到.
2.对称变换:(1)函数 的图像可以将函数
的图像可以将函数 的图像关于
的图像关于 轴对称即可得到;
轴对称即可得到;
(2)函数 的图像可以将函数
的图像可以将函数 的图像关于
的图像关于 轴对称即可得到;
轴对称即可得到;
(3)函数 的图像可以将函数
的图像可以将函数 的图像关于原点对称即可得到;
的图像关于原点对称即可得到;
(4)函数 的图像可以将函数
的图像可以将函数 的图像关于直线
的图像关于直线 对称得到.
对称得到.
3.翻折变换:(1)函数 的图像可以将函数
的图像可以将函数
 的图像的
的图像的 轴下方部分沿
轴下方部分沿 轴翻折到
轴翻折到 轴上
轴上
方,去掉原 轴下方部分,并保留
轴下方部分,并保留 的
的 轴上方
轴上方
部分即可得到;
(2)函数 的图像可以将函数
的图像可以将函数 的图像右边沿
的图像右边沿 轴翻折到
轴翻折到 轴左边替代原
轴左边替代原 轴左边部分并保留
轴左边部分并保留 在
在 轴右边部分即可得到.
轴右边部分即可得到.
 |
三.下列习题你必须掌握:
1.函数 与
与
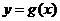 的图像如右图:
的图像如右图:
则函数
的图像可能是( )

2.函数y=-lg(x+1)的图象大致是

3.说明由函数 的图像经过怎样的图像变换得到函数
的图像经过怎样的图像变换得到函数 的图像.
的图像.
4.函数y=3sin(2x? )的图象,可看作是把函数y=3sin2x的图象作以下哪个平移得到
)的图象,可看作是把函数y=3sin2x的图象作以下哪个平移得到
(A)向左平移 (B)向右平移
(B)向右平移
(C)向左平移 (D)向右平移
(D)向右平移
5.若函数f(x)的图象经过点(-1,0),则函数f-1(x+4)的图象必过点
A (-1,4) B (-4,-1) C(-1,-4) D (1,4)
6.将函数 的图象按向量
的图象按向量 平移后的图象的解析式为
平移后的图象的解析式为 ,则
,则 等于( ).
等于( ).
A. B.
B.
C. D.
D.
 7.已知反比例函数y=
7.已知反比例函数y= 的图
的图
像如右图所示,则二次函数
y=2kx2-4x+k2的图像大致为( )

8.若函数 的图象与
的图象与 的图象关于
对称,则函数
的图象关于
对称,则函数 =
.
=
.
(注:填上你认为可以成为真命题的一种情形即可,不必考虑所有可能的情形)