郑州一中08―09学年度(下)期高2009级3月月考
数学(文)试题
本试卷分第I卷和第II卷两部分。满分150分。考试用时120分钟。考试结束后。将本试卷和答题卡一并交回。
http://www.lhjy.net.cn/
注意事项:
1.答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、座号、准考证号填写在答题卡和试题卷规定的位置上。
2.第I卷每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑;如需改
动,用橡皮擦干净后,再选涂其他答案标号。答案不能答在试题卷上。
3.第II卷必须用0.5毫米黑色签字笔作答,先划掉原来的答案,然后再写上新的答案;
不准使用涂改液、胶带纸、修正带。不按以上要求作答的答案无效。
第Ⅰ卷(选择题,共60分)
一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中只有一个选项是符合题目要求的。
1.设集合 ,则
,则  ( )
( )
A.{0} B.{2} C. D.
D.
2.正方体 中,
中, 、
、 、
、 分别是
分别是 、
、 、
、 的中点.那么,正
的中点.那么,正
|
 是公比为2的等比数列,则
是公比为2的等比数列,则 的值为
( )
的值为
( ) B.
B. C.
C. D.1
D.1 的最小正周期是
的最小正周期是 ②函数
②函数 在区间
在区间 上单调递增③
上单调递增③ 是函数
是函数 的图象的一条对称轴。其中正确的命题个数 ( )
的图象的一条对称轴。其中正确的命题个数 ( ) ,直线
,直线 与椭圆
与椭圆 恒有公共点,则实数
恒有公共点,则实数 的取值范围是
( )
的取值范围是
( ) B.
B. C.
C. D.
D.
 中,
中, 、
、 分别是棱
分别是棱 、
、 的中点,则直线
的中点,则直线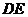 与平面
与平面 所成角的正弦值为
( )
所成角的正弦值为
( ) B.
B. C.
C. D.
D.
 ,下列结论中正确的是
( )
,下列结论中正确的是
( ) 是函数
是函数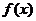 的极小值点,
的极小值点, 是极大值点;
是极大值点;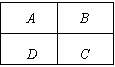 9.如图,在一个田字形区域
9.如图,在一个田字形区域 中涂色,要求同一区域涂同
一颜色,相邻区域涂不同颜色(
中涂色,要求同一区域涂同
一颜色,相邻区域涂不同颜色( 与
与 、
、 与
与 不相邻),现有4种颜色可供选择,则不同的涂色方案有
( )
不相邻),现有4种颜色可供选择,则不同的涂色方案有
( ) 10. 已知对称轴为坐标轴的双曲线的两条渐近线方程为
10. 已知对称轴为坐标轴的双曲线的两条渐近线方程为 ,若双曲线上有一点
,若双曲线上有一点 ,使
,使 ,则双曲线焦点 ( )
,则双曲线焦点 ( )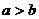 时,在x轴上 D.当
时,在x轴上 D.当 时,在y轴上
时,在y轴上 ,则在数列{an}的前50项中最小项和最大项分别是 ( )
,则在数列{an}的前50项中最小项和最大项分别是 ( ) ,
, B.
B. ,
,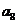 ,
, ,
, 在区间
在区间 内单调递增,则a的取值范围是 ( )
内单调递增,则a的取值范围是 ( ) B.
B. C.
C. D.
D.
 的展开式中的常数项为_____________(用数字作答).
的展开式中的常数项为_____________(用数字作答).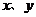 满足约束条件
满足约束条件 ,求
,求 的最大值为_____________.
的最大值为_____________. ,则
,则 __________.
__________. ,给出下列4个命题:
,给出下列4个命题: 时,
时, 只有一个实数根; ②
只有一个实数根; ② 时,
时, 是奇函数;
是奇函数; 对称; ④方程
对称; ④方程
 ,角B等于x,周长为y,求函数
,角B等于x,周长为y,求函数 ,发生基因突变的概率为
,发生基因突变的概率为 ,种子发芽与发生基因突变是两个相互独立事件.科学家在实验室对“太空种子”进行培育,从中选出优良品种.
,种子发芽与发生基因突变是两个相互独立事件.科学家在实验室对“太空种子”进行培育,从中选出优良品种. 

 满足,
满足, , 求
, 求 .
. . 是否存在最小正整数
. 是否存在最小正整数 , 有
, 有 恒成立?若存在,求出m的值;若不存在,请说明理由
恒成立?若存在,求出m的值;若不存在,请说明理由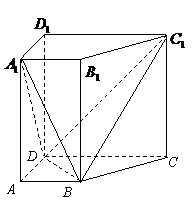 如图,已知在直四棱柱
如图,已知在直四棱柱 ,
, ,
,
 .
. 平面
平面 ;
; 的余弦值.
的余弦值. 在
在 上是增函数,在
上是增函数,在 上是减函数,且
上是减函数,且 .
. 时,求函数
时,求函数 .
. 是椭圆
是椭圆 的两个焦点,
的两个焦点, 为坐标原点,点
为坐标原点,点 在椭圆上,且
在椭圆上,且 ,⊙
,⊙ 为直径的圆,直线
为直径的圆,直线 :
: 与⊙
与⊙
 ,且满足
,且满足 时,求弦长
时,求弦长 的取值范围.
的取值范围. 16. ①②③
16. ①②③
 又
又

 (Ⅱ)
(Ⅱ)





 ,
, ,
, .
. ,则
,则 .
. 
 (Ⅰ)∵
(Ⅰ)∵ ,∴{
,∴{ }是公差为4的等差数列,
}是公差为4的等差数列, +4(n-1)=4n-3,∵an>0,∴an=
+4(n-1)=4n-3,∵an>0,∴an=

 ,由bn<
,由bn< ,得m>
,得m> ,
, 是
是 的中点,连结
的中点,连结 ,则四边形
,则四边形 为正方形,
为正方形, .故
.故 ,
, ,
, ,
, ,即
,即 .
. 又
又 ,
,
 平面
平面 ,
, 平面
平面 平面
平面 ,
, 的中点
的中点 , 连结
, 连结 ,又
,又 ,则
,则 .
. 的中点
的中点 ,连结
,连结 ,则
,则 ,
, .
. 为二面角
为二面角 的平面角.
的平面角. ,在
,在 中,
中, ,
, ,
, 的中点
的中点 ,连结
,连结 ,
, ,
, 中,
中, ,
, ,
, .
. .
. 二面角
二面角 .
. 为原点,
为原点, 所在直线分别为
所在直线分别为 轴,
轴, 轴,
轴, 轴建立如图所示的空间直角坐标系,则
轴建立如图所示的空间直角坐标系,则 ,
, ,
, ,
, ,
, ,
, .
.
 ,
, ,
,


 .
. 为平面
为平面 的一个法向量.
的一个法向量. ,
, ,
,
 取
取 ,则
,则 .
. ,
, 为平面
为平面 的一个法向量,
的一个法向量, ,
, ,得
,得 取
取 ,则
,则 ,
, 与
与 的夹角为
的夹角为 ,二面角
,二面角 ,显然
,显然 ,
, ,
, 在
在 上是增函数,在
上是增函数,在 上是减函数,
上是减函数,  时,
时,  即
即 .
. ,
, 得
得 ,
, ,
,








 时,函数
时,函数 ,
, 的两个根分别为
的两个根分别为 . ∵
. ∵ ,即
,即 ,
, .
. ,
, ,解得
,解得

 :
: 与⊙
与⊙ 相切,则
相切,则 ,即
,即 ,
, ,得
,得 ,
, 设
设
 ,
,
 ,
,
 ∴
∴ ,
,

 ,则
,则 ,
,
 在
在 上单调递增 ∴
上单调递增 ∴ .
.