2009届新课标物理考点预测(6)
动量
一、考点介绍
本考点是高考的必考内容,题型全面,选择题主要考查动量的矢量性,辨析“动量和动能”、“冲量与功”的基本概念;常设置一个瞬间碰撞的情景,用动量定理求变力的冲量;或求出平均力;或用动量守恒定律来判定在碰撞后的各个物体运动状态的可能值;计算题主要考查综合运用牛顿定律、能量守恒、动量守恒解题的能力;一般计算题具有过程错综复杂,图景“扑朔迷离”、条件隐晦难辨,知识覆盖广的特点,经常是高考的压轴题.
二、高考真题
1.(2008年山东卷.理综.38②)一个物体静置于光滑水平面上,外面扣一质量为M的盒子,如图1所示。现给盒子―初速度v0,此后,盒子运动的v-t图象呈周期性变化,如图2所示。请据此求盒内物体的质量。

图1 图2
2.(2008年海南卷.物理.19②)一置于桌面上质量为M的玩具炮,水平发射质量为m的炮弹.炮可在水平方向自由移动.当炮身上未放置其它重物时,炮弹可击中水平地面上的目标A;当炮身上固定一质量为M0的重物时,在原发射位置沿同一方向发射的炮弹可击中水平地面上的目标B.炮口离水平地面的高度为h.如果两次发射时“火药”提供的机械能相等,求B、A两目标与炮弹发射点之间的水平距离之比。
3.(2008年 广东卷.物理.20)如图3所示,固定的凹槽水平表面光滑,其内放置U形滑板N,滑板两端为半径R=
(1)P2在BC段向右滑动时,滑板的加速度为多大?
(2)BC长度为多少?N、P1和P2最终静止后,P1与P2间的距离为多少?
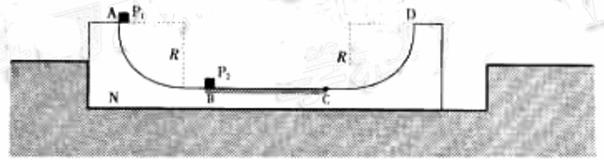
图3
4(2008年文东卷.物理.19)如图4(a)所示,在光滑绝缘水平面的AB区域内存在水平向右的电场,电场强度E随时间的变化如图4(b)所示.不带电的绝缘小球P2静止在O点.t=0时,带正电的小球P1以速度t0从A点进入AB区域,随后与P2发生正碰后反弹,反弹速度大小是碰前的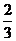 倍,P1的质量为m1,带电量为q,P2的质量m2=
倍,P1的质量为m1,带电量为q,P2的质量m2=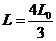 .已知
.已知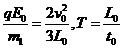 .
.
(1)求碰撞后小球P1向左运动的最大距离及所需时间.
(2)讨论两球能否在OB区间内再次发生碰撞.
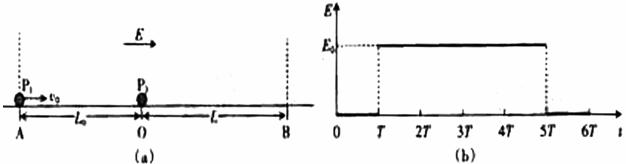
图4
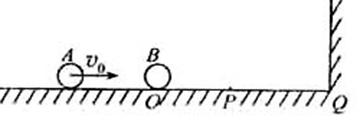
 5.(2007年宁夏卷.理综.30D)在光滑的水平面上,质量为m1的小球A以速率v0向右运动,在小球A的前方O点有一质量为m2的小球B处于静止状态,如图5所示。小球A与小球B发生正碰后小球A、B均向右运动,
5.(2007年宁夏卷.理综.30D)在光滑的水平面上,质量为m1的小球A以速率v0向右运动,在小球A的前方O点有一质量为m2的小球B处于静止状态,如图5所示。小球A与小球B发生正碰后小球A、B均向右运动,
小球B被在Q点处的墙壁弹回后与小球A在P点相遇,PQ=1.5PO。假设小球间的碰撞及小球与墙壁之间的碰撞都是弹性的,求两小球质量之比m1 /m2。
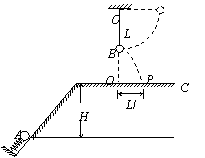
6.(2007年广东卷.物理.17)如图6所示,在同一竖直平面上,质量为
已知球B质量为m,悬绳长L,视两球为质点。重力加速度为g,不计空气阻力。求:⑴球B在两球碰撞后一瞬间的速度大小;⑵球A在两球碰撞后一瞬间的速度大小;⑶弹簧的弹性力对球A所做的功。
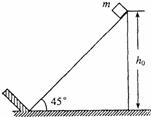 7.(2008年四川卷.理综.24)一倾角为θ=45°的斜面固定于地面,斜面顶端离地面的高度h0=
7.(2008年四川卷.理综.24)一倾角为θ=45°的斜面固定于地面,斜面顶端离地面的高度h0=
图7
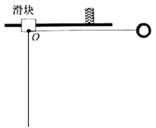 8.(2008年全国卷.理综.24)图8中滑块和小球的质量均为m,滑块可在水平放置的光滑固定导轨上自由滑动,小球与滑块上的悬点O由一不可伸长的轻绳相连,轻绳长为l。开始时,轻绳处于水平拉直状态,小球和滑块均静止。现将小球由静止释放,当小球到达最低点时,滑块刚好被一表面涂有粘性物质的固定挡板粘住,在极短的时间内速度减为零,小球继续向左摆动,当轻绳与竖直方向的夹角θ=60°时小球达到最高点。求
8.(2008年全国卷.理综.24)图8中滑块和小球的质量均为m,滑块可在水平放置的光滑固定导轨上自由滑动,小球与滑块上的悬点O由一不可伸长的轻绳相连,轻绳长为l。开始时,轻绳处于水平拉直状态,小球和滑块均静止。现将小球由静止释放,当小球到达最低点时,滑块刚好被一表面涂有粘性物质的固定挡板粘住,在极短的时间内速度减为零,小球继续向左摆动,当轻绳与竖直方向的夹角θ=60°时小球达到最高点。求
(1)从滑块与挡板接触到速度刚好变为零的过程中,挡板阻力对滑块的冲量;
(2)小球从释放到第一次到达最低点的过程中,绳的拉力对小球做功的大小。 图8
9.(2008年天津卷.理综.25)光滑水平面上放着质量mA=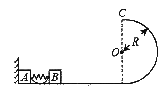 /s2,求
/s2,求
(1)绳拉断后瞬间B的速度vB的大小;
(2)绳拉断过程绳对B的冲量I的大小;
(3)绳拉断过程绳对A所做的功W。
图9
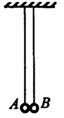 10.(2008年宁夏卷.物理.32②)某同学利用如图10所示的装置验证动量守恒定律。图中两摆摆长相同,悬挂于同一高度,A、B两摆球均很小,质量之比为1∶2。当两摆均处于自由静止状态时,其侧面刚好接触。向右上方拉动B球使其摆线伸直并与竖直方向成45°角,然后将其由静止释放。结果观察到两摆球粘在一起摆动,且最大摆角成30°。若本实验允许的最大误差为±4%,此实验是否成功地验证了动量守恒定律?
图10
10.(2008年宁夏卷.物理.32②)某同学利用如图10所示的装置验证动量守恒定律。图中两摆摆长相同,悬挂于同一高度,A、B两摆球均很小,质量之比为1∶2。当两摆均处于自由静止状态时,其侧面刚好接触。向右上方拉动B球使其摆线伸直并与竖直方向成45°角,然后将其由静止释放。结果观察到两摆球粘在一起摆动,且最大摆角成30°。若本实验允许的最大误差为±4%,此实验是否成功地验证了动量守恒定律?
图10
三、名校试题
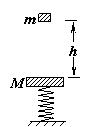 1.(
(广东省2009届新洲中学高三摸底考试试卷.物理.15)如图11所示,质量为M=
1.(
(广东省2009届新洲中学高三摸底考试试卷.物理.15)如图11所示,质量为M=
继续下降了l2=
略不计,弹簧的形变始终在弹性限度内,重力加速度取g=
(1)弹簧的劲度系数k.
(2)从木块和铁板共同开始向下运动到它们的共同速度第一
次减小到零的过程中,弹簧的弹性势能增加了多少? 图11
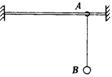
2.(山东青岛市高三第一次质检卷.物理.31)如图12所示,物体A、B的质量分别是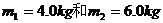 ,用轻弹簧相连结放在光滑的水平面上,物体B左侧与竖直墙相接触。另有一个物体C从t=0时刻起以一定的速度向左运动,在t=0.5s时刻与物体A相碰,碰后立即与A粘在一起不再分开。物体C的v ? t图象如图13所示。试求:
,用轻弹簧相连结放在光滑的水平面上,物体B左侧与竖直墙相接触。另有一个物体C从t=0时刻起以一定的速度向左运动,在t=0.5s时刻与物体A相碰,碰后立即与A粘在一起不再分开。物体C的v ? t图象如图13所示。试求:
①物块C的质量m3;
②在5.0s到15s的时间内物块A的动量变化的大小和方向。
|
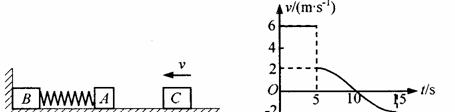
 平速度V0=
平速度V0= 以水平速度v0=
以水平速度v0= 5.(广东中山龙山中学2009届高三第二次月考试卷.物理.18)如图16所示,EF为水平地面,O点左侧是粗糙的、
5.(广东中山龙山中学2009届高三第二次月考试卷.物理.18)如图16所示,EF为水平地面,O点左侧是粗糙的、 右侧是光滑的。一轻质弹簧右端与墙壁固定,左端与静止在O点质量为m的小物块A连结,弹簧处于原长状态。质量为m的物块B在大小为F的水平恒力的作用下由C处从静止开始向左运动,已知物块B与地面EO段间的滑动摩擦力大小为
右侧是光滑的。一轻质弹簧右端与墙壁固定,左端与静止在O点质量为m的小物块A连结,弹簧处于原长状态。质量为m的物块B在大小为F的水平恒力的作用下由C处从静止开始向左运动,已知物块B与地面EO段间的滑动摩擦力大小为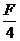 ,物块B运动到O点与物块A相碰并一起向右运动(设碰撞时间极短),运动到D点时撤去外力F。已知CO = 4S,OD = S。求撤去外力后:
图16
,物块B运动到O点与物块A相碰并一起向右运动(设碰撞时间极短),运动到D点时撤去外力F。已知CO = 4S,OD = S。求撤去外力后:
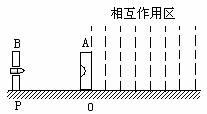
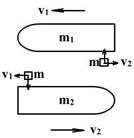
图16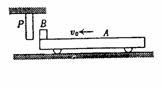 6.(湖南长郡中学2009届高三第二次月考试题.物理.18)如图17所示,P是固定的竖直挡板,A是置于光滑水平面上的平板小车(小车表面略低于档板下端),B是放在小车最左端表面上的小物块.开始时,物块随小车一起以相同的水平速度向左运动,接着物块与挡板发生了第一次碰撞,碰后物块相对于车静止时的位置离小车最左端的距离等于车长的
6.(湖南长郡中学2009届高三第二次月考试题.物理.18)如图17所示,P是固定的竖直挡板,A是置于光滑水平面上的平板小车(小车表面略低于档板下端),B是放在小车最左端表面上的小物块.开始时,物块随小车一起以相同的水平速度向左运动,接着物块与挡板发生了第一次碰撞,碰后物块相对于车静止时的位置离小车最左端的距离等于车长的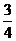 .此后物块又与挡板发生了多次碰撞,最后物块恰未从小车上滑落.若物体与小车表面间的动摩擦因数是个定值,物块与挡板发生碰撞时无机械能损失且碰撞时间极短,
图17
.此后物块又与挡板发生了多次碰撞,最后物块恰未从小车上滑落.若物体与小车表面间的动摩擦因数是个定值,物块与挡板发生碰撞时无机械能损失且碰撞时间极短,
图17
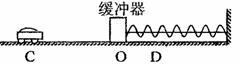 9.(山东省济南一中高三期中测试卷.物理.15)在赛车场上,为了安全起见,在车道外围一定距离处一般都放有废旧的轮胎组成的围栏。在一次比较测试中,将废旧轮胎改为由弹簧连接的缓冲器,缓冲器与墙之间用轻绳束缚。如图19所示,赛车从C处由静止开始运动,牵引力恒为F,到达O点与缓冲器相撞(设相撞时间极短),而后他们一起运动到D点速度变为零,此时发动机恰好熄灭(即牵引力变为零)。已知赛车与缓冲器的质量均为m,OD相距为S,CO相距4S,赛车运动时所受地面摩擦力大小始终为
9.(山东省济南一中高三期中测试卷.物理.15)在赛车场上,为了安全起见,在车道外围一定距离处一般都放有废旧的轮胎组成的围栏。在一次比较测试中,将废旧轮胎改为由弹簧连接的缓冲器,缓冲器与墙之间用轻绳束缚。如图19所示,赛车从C处由静止开始运动,牵引力恒为F,到达O点与缓冲器相撞(设相撞时间极短),而后他们一起运动到D点速度变为零,此时发动机恰好熄灭(即牵引力变为零)。已知赛车与缓冲器的质量均为m,OD相距为S,CO相距4S,赛车运动时所受地面摩擦力大小始终为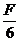 ,缓冲器的底面光滑,可无摩擦滑动,在O点时弹簧无形变。问:
,缓冲器的底面光滑,可无摩擦滑动,在O点时弹簧无形变。问: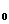 ,2 v
,2 v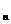 ;
; (2)第1号物块与木板刚好相对静止时的速度v
(2)第1号物块与木板刚好相对静止时的速度v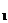 ;
;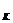 图20
图20 ,则该空间站轨道半径
,则该空间站轨道半径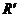 为多大?
为多大? 内探测器的质量变化较小,可以忽略不计.求喷气
内探测器的质量变化较小,可以忽略不计.求喷气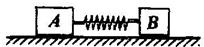 1 .如图21所示,在光滑的水平面上,木块A、B通过细绳将一轻弹簧夹紧.现将细绳烧断,A、B分别向左、右运动,若mA:mB=2:1,则EKa:EKb=?
1 .如图21所示,在光滑的水平面上,木块A、B通过细绳将一轻弹簧夹紧.现将细绳烧断,A、B分别向左、右运动,若mA:mB=2:1,则EKa:EKb=?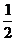 mv2
mv2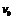 速度行驶,船上有两个质量皆为m的小孩a和b,分别静止站在船头和船尾。现小孩a沿水平方向以速率
速度行驶,船上有两个质量皆为m的小孩a和b,分别静止站在船头和船尾。现小孩a沿水平方向以速率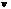 (相对于静止的水面)向前跳入水中,然后小孩b沿水平方向以同一速率
(相对于静止的水面)向前跳入水中,然后小孩b沿水平方向以同一速率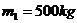 ,
,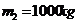 。问而在交换麻袋前两只船的速率为多少?(水的阻力不计)
。问而在交换麻袋前两只船的速率为多少?(水的阻力不计)
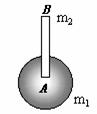 8.图23是一个演示实验,它显示:图中自由下落的物体A和B经反弹后,B能上升到比初始位置高得多的地方。A是某种材料组成的空心球,质量为m1=
8.图23是一个演示实验,它显示:图中自由下落的物体A和B经反弹后,B能上升到比初始位置高得多的地方。A是某种材料组成的空心球,质量为m1=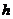 的水平桌面边缘,质量为
的水平桌面边缘,质量为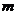 的小物块B沿桌面向A运动并以速度
的小物块B沿桌面向A运动并以速度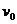 与之发现正撞(碰撞时间极短)。然后A离开桌面,其落地点离出发点的水平距离为
与之发现正撞(碰撞时间极短)。然后A离开桌面,其落地点离出发点的水平距离为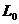 ,碰后B反向运动,求B后退的距离。已知B与桌面间的动摩擦因数为
,碰后B反向运动,求B后退的距离。已知B与桌面间的动摩擦因数为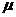 ,重力加速度为
,重力加速度为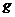 。
。 10。如图24所示,质量为m的有孔物体A套在光滑的水平杆上,在A下面用细绳拴一质量为
10。如图24所示,质量为m的有孔物体A套在光滑的水平杆上,在A下面用细绳拴一质量为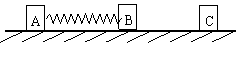
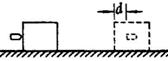 12.如图26所示,质量m的子弹以v0初速度水平射入放在光滑水平面上质量M的木块.子弹射入木块d深度后便随木块一起运动,试求木块对子弹平均阻力的大小.
图26
12.如图26所示,质量m的子弹以v0初速度水平射入放在光滑水平面上质量M的木块.子弹射入木块d深度后便随木块一起运动,试求木块对子弹平均阻力的大小.
图26 13.如图27所示,长木板
13.如图27所示,长木板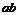 的
的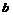 端固定一挡板,木板连同挡板的质量
端固定一挡板,木板连同挡板的质量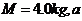 、
、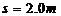 ,木板位于光滑水平面上,在木板
,木板位于光滑水平面上,在木板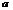 端有一小物块,其质量
端有一小物块,其质量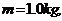 小物块与木板间的动摩擦因数
小物块与木板间的动摩擦因数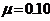 ,他们都处于静止状态。现令小物块以初速度
,他们都处于静止状态。现令小物块以初速度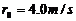 沿木板向前滑动,直到和挡板相碰。碰撞后,小物块恰好回到
沿木板向前滑动,直到和挡板相碰。碰撞后,小物块恰好回到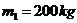 的石板压在演员身上,另一个演员举起质量
的石板压在演员身上,另一个演员举起质量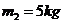 的铁锤,使劲地向石板咂去的瞬间,石板被砸碎了,而演员安然无恙,试通过分析和必要的理论计算来说明其中的奥妙。
的铁锤,使劲地向石板咂去的瞬间,石板被砸碎了,而演员安然无恙,试通过分析和必要的理论计算来说明其中的奥妙。

 17.在纳米技术中需要移动或修补原子,必须使在不停地做热运动(速率约为几百米每秒)的原子几乎静止下来且能在一个小的空间区域内停留一段时间,为此发明了“激光致冷”技术。若把原子和入射光子分别类比为一辆小车和一个小球,则“激光致冷”与下述力学模型很类似:一辆质量为m的小车(一侧固定一轻弹簧),以如图27所示速度v0水平向右运动,一个动量大小为p,质量可以忽略的小球水平向左射入小车并压缩弹簧至最短,接着被锁定一段时间△T,再解除锁定后使小球以大小相同的动量p水平向右弹出,紧接着不断重复上述过程,最终小车停下来。设地面和车厢均光滑,除锁定时间△T外,不计小球在小车上运动和弹簧压缩、伸长时间,求:
17.在纳米技术中需要移动或修补原子,必须使在不停地做热运动(速率约为几百米每秒)的原子几乎静止下来且能在一个小的空间区域内停留一段时间,为此发明了“激光致冷”技术。若把原子和入射光子分别类比为一辆小车和一个小球,则“激光致冷”与下述力学模型很类似:一辆质量为m的小车(一侧固定一轻弹簧),以如图27所示速度v0水平向右运动,一个动量大小为p,质量可以忽略的小球水平向左射入小车并压缩弹簧至最短,接着被锁定一段时间△T,再解除锁定后使小球以大小相同的动量p水平向右弹出,紧接着不断重复上述过程,最终小车停下来。设地面和车厢均光滑,除锁定时间△T外,不计小球在小车上运动和弹簧压缩、伸长时间,求:

 联立以上两式解得 m=M
联立以上两式解得 m=M








 ,由机械能守恒定律有:
,由机械能守恒定律有:  解得:
解得:
 、
、



 (向左)
(向左)

 ,所以假设成立。
,所以假设成立。 得
得
 解得:
解得:





 (2)
(2)


 (水平向左)
(水平向左)  (水平向右)
(水平向右) 又:
又:


 时间在OB区间内再次发生碰撞,且P1受电场力不变,由运动学公式,以水平向右为正:
时间在OB区间内再次发生碰撞,且P1受电场力不变,由运动学公式,以水平向右为正: 则:
则:
 (故P1受电场力不变)
(故P1受电场力不变)

 和
和 ,在碰撞过程中动量守恒,碰撞前后动能相等,有
,在碰撞过程中动量守恒,碰撞前后动能相等,有 ………… ①
………… ① ………… ②
………… ② ,可解出 m1∶m2=2∶1
,可解出 m1∶m2=2∶1 。
。  ,可得vA= v0/3,vB=
4v0/3,因此
,可得vA= v0/3,vB=
4v0/3,因此 ,同时也得到
,同时也得到 。
。  ,解得W=
,解得W= 
 ①
① ②
②
 ③
③
 ④
④  ⑤
⑤
 ⑥式中
⑥式中  ⑦
⑦
 ⑧总冲量为
⑧总冲量为  ⑨
⑨ ⑩得
⑩得 ⑾
⑾ N?s
N?s
 ,到达C点时的速度为
,到达C点时的速度为 ,有
,有 (1)
(1) (2)
(2) (3)
(3) ,取水平向右为正方向,有
,取水平向右为正方向,有 (4)
(4) (5)
(5) 其大小为4NS (6)
其大小为4NS (6) ,取水平向右为正方向,有
,取水平向右为正方向,有 (7)
(7) 代入数据得
代入数据得
 、
、 ,摆长为l,B球的初始高度为h1,碰撞前B球的速度为vB.在不考虑摆线质量的情况下,根据题意及机械能守恒定律得
,摆长为l,B球的初始高度为h1,碰撞前B球的速度为vB.在不考虑摆线质量的情况下,根据题意及机械能守恒定律得 ①
① ②
② ④
④ ⑤
⑤
 由此可以推出
由此可以推出 ≤4%
≤4%
 mv02
mv02  …
…

 ,由动能定理有:
,由动能定理有:

 ,由系统动量守恒得:
,由系统动量守恒得: (2分)
(2分) 解得:
解得:






 ,由机械能守恒得
,由机械能守恒得



 (2)
(2) L+
L+ =
= mv02=E
解得 v0=
mv02=E
解得 v0=







 ②
2分
②
2分
 ③
③ 
 ④
④  ⑤
⑤
 ⑥
⑥ 
 ,因木板与所有物块系统水平方向不受外力,动量守恒,应有:
,因木板与所有物块系统水平方向不受外力,动量守恒,应有: +m?2 v
+m?2 v (n+1)v
(n+1)v ,取木板与物块1为系统一部分,第2 号物块到第n号物块为系统另一部分,则
,取木板与物块1为系统一部分,第2 号物块到第n号物块为系统另一部分,则 =(n-1)m?(v
=(n-1)m?(v ,则第k号物块速度由k v
,则第k号物块速度由k v (k+1)m v
(k+1)m v








 ,可得:
,可得:


 ,根据动量定理
,根据动量定理 ,而
,而 ,所以P=
,所以P= ,故选项A正确。
,故选项A正确。 ①
①
 ②
②  ③
③
 ④
④  ⑤
⑤  ,代入数据得
,代入数据得 .
. 为正方向,设a向前跳入水中后,船速为
为正方向,设a向前跳入水中后,船速为 ,有:
,有:  ①
① ,则
,则 ②
② ,方向与
,方向与 也解得
也解得 ①
① ②
② 1 m/s
1 m/s  9 m/s
9 m/s ③
③ ……①
……① 为A从离开桌面至落
为A从离开桌面至落