浙江杭州二中2008学年高三年级第五次月考
数学试卷(理科)
第I卷(共50分)
命题:徐存旭 校对:陆华兵
一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的. 
1.已知集合
 ,那么集合
,那么集合 中
( )
中
( )
A.没有一个元素
B.至多一个元素 
C.只有两个元素
D.有一个或两个元素 
2.已知点 都在直线
都在直线 上,那么在数列
上,那么在数列 中有
( )
中有
( )
A. B.
B. C.
C. D.
D.

 3.为了解某校高三学生的视力情况,随机地抽查了该校100名高三学生的视力情况,得到频率分布直方图,如右图,由于不慎将部分数据丢失,但知道前4组的频数成等比数列,后6组的频数成等差数列,设最大频率为a,视力在4.6到5.0之间的学生数为b,则a, b的值分别为
( )
3.为了解某校高三学生的视力情况,随机地抽查了该校100名高三学生的视力情况,得到频率分布直方图,如右图,由于不慎将部分数据丢失,但知道前4组的频数成等比数列,后6组的频数成等差数列,设最大频率为a,视力在4.6到5.0之间的学生数为b,则a, b的值分别为
( )
A.0.27,78 B.0.27,83
C.2.7,78
D.2.7,83
|

 个连续自然数按规律排成下表根据规律,从
个连续自然数按规律排成下表根据规律,从 到
到 的箭头方向依次为( )
的箭头方向依次为( ) A.
A. B.
B. 
 D.
D. 
 ”与命题“
”与命题“ 或
或 ”都是真命题,那么命题
”都是真命题,那么命题 ,则
,则 ”的否命题是:“若
”的否命题是:“若 ,则
,则 ”
” ,则
,则
 ”是“
”是“ ”的充分不必要条件
”的充分不必要条件 是定义在
是定义在 上的非负可导函数,且满足
上的非负可导函数,且满足 ,对任意的正数
,对任意的正数 ,若
,若 ,则必有
( )
,则必有
( ) B.
B.
 D.
D.
 ,两焦点为
,两焦点为 ,抛物线C以
,抛物线C以 为顶点,
为顶点, 为焦点,P为两
为焦点,P为两 ,则
,则 B.
B. C.
C. D.
D.
 的函数
的函数
 ,若关于
,若关于 的方程
的方程 有且仅有三个不同的实数解
有且仅有三个不同的实数解 ,则
,则 ( )
( ) B.
B.
 二、填空题:本大题共7小题,每小题4分,共28分.
二、填空题:本大题共7小题,每小题4分,共28分.
 化简后的结果为
.
化简后的结果为
. ,
, ,利用如图所示
,利用如图所示 展开式中常数项的值为
.
展开式中常数项的值为
. ,又
,又 ,
, 且
且 的最小值等于
的最小值等于 ,则正数
,则正数 的值为__________.
的值为__________. 所表示的区域为
所表示的区域为 ,现在区域
,现在区域 上方的概率为 .
上方的概率为 .  都是负实数,则
都是负实数,则 的最小值是
.
的最小值是
.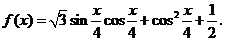
 ,满足
,满足 求函数
求函数 的取值范围.
的取值范围. .现在甲、乙两人从袋中轮流摸取1球,甲先取,乙后取,然后甲再取,……,取后不放回,直到两人中有一人取到白球时即终止.每个球在每一次被取出的机会是等可能的,用
.现在甲、乙两人从袋中轮流摸取1球,甲先取,乙后取,然后甲再取,……,取后不放回,直到两人中有一人取到白球时即终止.每个球在每一次被取出的机会是等可能的,用 表示取球终止时所需要的取球次数.
表示取球终止时所需要的取球次数. ;
; 的各项都是正数,
的各项都是正数, ,
, .
. 的通项公式;
的通项公式; .
. 满足到点
满足到点 的距离比到直线
的距离比到直线 的距离小1.
的距离小1. 的直线与曲线C交于A、B两点,在线段AB上取点
的直线与曲线C交于A、B两点,在线段AB上取点 ,满足
,满足 ,证明:
,证明: ;(?)点
;(?)点 ,
, ,其中
,其中 .设两曲线
.设两曲线 ,
, 有公共点,且在该点处的切线相同.
有公共点,且在该点处的切线相同. 表示
表示 ,并求
,并求 (
( ).
). ;
12.
;
12.  (或
(或 ); 13. 15;
14. 6;
); 13. 15;
14. 6;  16.
16.  ;
17.
;
17. 
 三、解答题
三、解答题
 …………12′
…………12′ 故函数
故函数 的取值范围是
的取值范围是 …………12′
…………12′  ,所以
,所以 =12,
=12, ),即袋中原有4个白球;
…………4′
),即袋中原有4个白球;
…………4′ 的可能取值为1,2,3,4
的可能取值为1,2,3,4
 所以,取球次数
所以,取球次数



 …………9′
…………9′  或 “
或 “ …………14′
…………14′  ∴
∴ ∵
∵ ∴
∴ ∴
∴ 为等比数列∴
为等比数列∴ …………4′
…………4′ 得
得 
 ∴
∴  …………9′
⑶∵
…………9′
⑶∵

 即
即 ),∴
),∴ 为递增数列.
为递增数列.
 从而
从而

 …………14′
…………14′ ,由显然
,由显然 ,得
,得 ,化简得
,化简得 ;
…………5′
;
…………5′ 



 …………10′
…………10′  ,不妨设点A在点P与点B之间,点
,不妨设点A在点P与点B之间,点 ,依(?)有
,依(?)有 *,又可设过点P(2,4)的直线方程为
*,又可设过点P(2,4)的直线方程为 ,得
,得 ,
, ,代入上*式得
,代入上*式得 ,又
,又 ,得
,得 ,当直线AB的斜率不存在时,也满足上式.即点Q总过直线
,当直线AB的斜率不存在时,也满足上式.即点Q总过直线 与
与 在公共点
在公共点 处的切线相同.
处的切线相同. ,
, ,由题意
,由题意 ,
, .即
.即 由
由 得:
得: ,或
,或 (舍去).即有
(舍去).即有 .
…………4′
.
…………4′ ,则
,则 .于是当
.于是当 ,即
,即 时,
时, ;
; ,即
,即 时,
时, .故
.故 在
在 为增函数,在
为增函数,在 为减函数,于是
为减函数,于是 的最大值为
的最大值为 .
…………8′
.
…………8′

 .故
.故 在
在 为减函数,在
为减函数,在 为增函数,于是函数
为增函数,于是函数 .故当
.故当 时,有
时,有 ,即当
,即当