唐山一中2009届高三年级数学仿真训练考试卷 (一)
数学
说明:1.本试卷共四页,包括三道大题,22道小题,共150分。其中第一道大题为选择题。
2.所有答案请在答题卡上作答,在本试卷和草稿纸上作答无效。答题前请仔细阅读答题卡上的“注意事项”,按照“注意事项”的规定答题。
一、选择题:(本大题共12小题,每小题5分,共60分,每小题给出的四个选项中,只有一项是符合题目要求的).
1.已知集合A={x|y=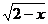 }, B={y|y=
}, B={y|y=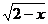 },则A∩B=
},则A∩B=
A.Æ B.R
C.(-∞,2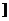 D.[0,2]
D.[0,2]
2.已知cos130°=a,则tan50°=
A.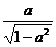 B.
B.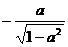 C.
C.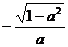 D.
D.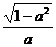
3.已知数列{an}中,a1=1,an=an+1+2(n≥1),则a100=
A.199
B.
4.(理科)已知i是虚数单位,(1+2i)z1=-1+3i,z2=1+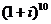 ,z1、z2在复平面上对应的点分别为A、B,O为坐标原点,则
,z1、z2在复平面上对应的点分别为A、B,O为坐标原点,则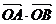 =
=
A.33 B.
(文科)已知直线l:4x+3y-5=0与圆C:x2+y2-4=0交于A、B两点,O为坐标原点,则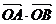 =
=
A.-2 B.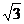 D. 2
D. 2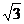
5.(理科)已知函数f(x)=xlnx2 (x<-1)的导函数为g(x),则g(x)的反函数是
A.y=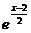 (x<2) B.y=
(x<2) B.y=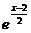 (x>2)
C.y=-
(x>2)
C.y=-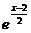 (x>2) D.y=-
(x>2) D.y=-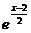 (x<2)
(x<2)
(文科)y=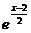 +2(x>2)的反函数是
+2(x>2)的反函数是
A.y=2ln(x-2)+2 (x>2) B.y=ln(x-2)2+2 (x≠2)
C.y=ln(ex-2e)2 (x>3) D.y=ln(ex-2e)2 (x<3)
6.已知定点F1、F2和动点P满足|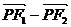 |=2,|
|=2,|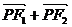 |=4,则点P的轨迹为
|=4,则点P的轨迹为
A.椭圆 B.圆 C.直线 D.线段
7.已知线性约束条件: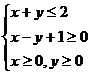 ,则z = x ? 2y的最大值和最小值分别是
,则z = x ? 2y的最大值和最小值分别是
 A.0和? 4
B.2和
? 4 C.2和 ?
A.0和? 4
B.2和
? 4 C.2和 ?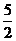 D.1 和 0
D.1 和 0
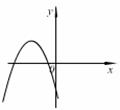
8.已知二次函数f(x)=ax2+bx+c的图象与x轴有两个交点,且与x轴、y轴的交点都在负半轴上(如图),则一定有
A.b∈(-∞,0) B.b∈(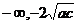 )
)
C.b∈(0,+∞)
D.b∈(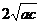 ,+∞)
,+∞)
9.已知a、b、c是三条不同的直线,命题“a∥b且a⊥c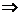 b⊥c”是正确的,如果把a、b、c中的两个或三个换成平面,在所得的命题中,真命题有
b⊥c”是正确的,如果把a、b、c中的两个或三个换成平面,在所得的命题中,真命题有
A.1个 B.2个 C.3个 D.4个
10.椭圆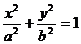 (a>b>0)的短轴长是常数,当两准线间的距离取得最小值时,椭圆的离心率为
(a>b>0)的短轴长是常数,当两准线间的距离取得最小值时,椭圆的离心率为
A.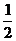 B.
B.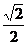 C.
C.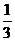 D.
D.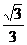
11. 对于函数f(x)=x3cos3(x+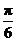 ),下列说法正确的是
),下列说法正确的是
A.f(x)是奇函数且在(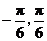 )上递减
)上递减
B. f(x)是奇函数且在(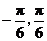 )上递增
)上递增
C. f(x)是偶函数且在(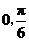 )上递减
)上递减
D.f(x)是偶函数且在(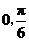 )上递增
)上递增
12.已知A、B是球O表面上两点,AB=8.过AB作两个平面α、β,使球心O在平面α
上,且O到平面β的距离为2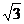 .如果二面角α―AB―β=60°,那么A、B两点间的球面距离为
.如果二面角α―AB―β=60°,那么A、B两点间的球面距离为
A.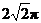 B.
B.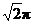 C.
C.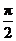 D.
D.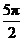
二、填空题:(本大题共4小题,每小题5分,共20分).
13.(理科)某篮球运动员在3分线内、外投蓝的命中率分别为0.7和0.4.在一场比赛中,如果该运动员在3分线内、外分别投蓝10次和5次,则该运动员得分的期望是______分.(注:在3分线内投中1球得2分,在3分线外投中1球得3分)
(文科)在集合{-4,-3,-2,-1,1,2,3,4}中任取两个元素x1和x2.抛物线x2=4y在
x1、x2对应点处的切线分别为l1、l2,则l1、l2互相垂直的概率为________.
14.在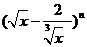 的展开式中,只有第5项的二项式系数最大,则展开式中含
的展开式中,只有第5项的二项式系数最大,则展开式中含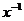 项为第_____项.
项为第_____项.
 15.已知双曲线
15.已知双曲线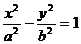 (a>0,b>0)的右焦点为F,过F且斜率为
(a>0,b>0)的右焦点为F,过F且斜率为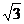 的直线l与右准线的交点P在该双曲线的渐近线上,则此双曲线的两条渐近线的夹角为_____.
的直线l与右准线的交点P在该双曲线的渐近线上,则此双曲线的两条渐近线的夹角为_____.
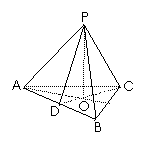
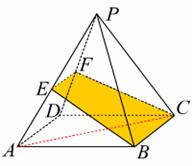
16.在正三棱锥P―ABC中,O是底面中心,PD是斜高(如图),
小棱锥P―AOD中集中了正棱锥的许多重要元素,研究表明:在
PO、PD、PA、OA、OD、AD、∠PDO、∠PAO、∠PAD中,已知
两个不全为角、也不全在底面AOD上的量,就可以求出其它各量.如果不考虑结论的变化,仅考虑两个已知条件的搭配情况,那么
能编制_______种不同类型(如:已知PA、PD与已知PA、PO算
作不同类型.用数字作答)的题目.
三、解答题:(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤).
17.(本小题满分10分)在△ABC中,sinA+cosA=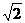 ,sinB-cosB=
,sinB-cosB=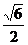 ,BC=2.
,BC=2.
(Ⅰ)求∠C; (Ⅱ)求△ABC的面积.
18.(本小题满分12分)
有标号分别为1、2、3的三个电子元件,事件A、B、C分别表示“元件1损坏”、“元件2损坏”和“元件3损坏”(损坏的元件不再导电).事件D表示“电路两端有电流通过”.
 (Ⅰ)分别就下列三种电路,用事件A、B、C(或其对立事件)表示事件D(每种电路只写出一种表示即可);
(Ⅰ)分别就下列三种电路,用事件A、B、C(或其对立事件)表示事件D(每种电路只写出一种表示即可);
|
 (Ⅱ)若元件1、2、3损坏的概率分别为0.1、0.2和0.3,求上面三种电路中,事件D发生的概率.根据计算推断,家用照明电路采用的是哪种联法?(假设每个元件的损坏与否是互不影响的)
(Ⅱ)若元件1、2、3损坏的概率分别为0.1、0.2和0.3,求上面三种电路中,事件D发生的概率.根据计算推断,家用照明电路采用的是哪种联法?(假设每个元件的损坏与否是互不影响的)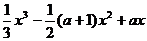 (a∈R).
(a∈R).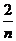 +1)an(n≥1).
+1)an(n≥1).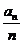 }是等比数列;
}是等比数列;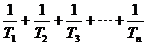 .
.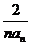 的大小
的大小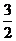 )、A、B在椭圆E上,且
)、A、B在椭圆E上,且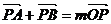 (m∈R).
(m∈R). 的定义域,A=
的定义域,A= ,B表示函数y=
,B表示函数y= ,所以A∩B=[0,2].
,所以A∩B=[0,2]. ,所以tan50°=
,所以tan50°= .
. =1+i,z2=1+(2i)5=1+32i,∴A(1,1)、B(1,32).
=1+i,z2=1+(2i)5=1+32i,∴A(1,1)、B(1,32). =1×1+1×32=33.
=1×1+1×32=33. =1,圆的半径为2,设弦AB的中点为C,则∠AOC=60°,∠AOB=120°.
=1,圆的半径为2,设弦AB的中点为C,则∠AOC=60°,∠AOB=120°. =2 ln(-x)+2 (x<-1) . g(x)的值域是y>2,反解得 -x=
=2 ln(-x)+2 (x<-1) . g(x)的值域是y>2,反解得 -x= ( y>2),g-1(x)=-
( y>2),g-1(x)=- ( x>2),故选C.
( x>2),故选C. 6.B 解法1:如图
6.B 解法1:如图 ,
, ,|
,| |=2,
|=2,
 =(-1-x,-y),
=(-1-x,-y), =(1-x,-y)
=(1-x,-y) ,
,
 ,轨迹为圆.
,轨迹为圆. .
. 7.C不等式组
7.C不等式组 表示的平面区域(如图).
表示的平面区域(如图).  )处时,z=x-2y取最小值
)处时,z=x-2y取最小值 .
. ,得b<0.又图象与x轴有两个交点,所以,△=b2-4ac>0,解得
,得b<0.又图象与x轴有两个交点,所以,△=b2-4ac>0,解得 或
或 ,但b<0,因此选B.
,但b<0,因此选B. β⊥c”,是真命题.把a换成平面α,把c换成平面γ,得到命题:“α∥b,α⊥γ
β⊥c”,是真命题.把a换成平面α,把c换成平面γ,得到命题:“α∥b,α⊥γ =4b.
=4b. ,即b=c.此时a=
,即b=c.此时a= c,e=
c,e= .
. )=-x3 sin3x.∵y=x3和y=sin3x都是奇函数,且在(
)=-x3 sin3x.∵y=x3和y=sin3x都是奇函数,且在( )上都是增函数,∴f(x) =-x3 sin3x是偶函数,且在(
)上都是增函数,∴f(x) =-x3 sin3x是偶函数,且在( 12.A 如图,作OO1⊥β,O1为垂足,取AB中点C,连接OC,O1C,则OC⊥AB,O1C⊥AB,∠O1CO是二面角α―AB―β的平面角,所以∠O1CO=60°.在Rt△OO1C中,OO1=2
12.A 如图,作OO1⊥β,O1为垂足,取AB中点C,连接OC,O1C,则OC⊥AB,O1C⊥AB,∠O1CO是二面角α―AB―β的平面角,所以∠O1CO=60°.在Rt△OO1C中,OO1=2 ,OC=
,OC= =4.
=4. .
. 抛物线方程化为y=
抛物线方程化为y= ,y’=
,y’= x. l1、l2的斜率分别为
x. l1、l2的斜率分别为 .
. ,令
,令 ,得r=6,
,得r=6, 的交点坐标为P(
的交点坐标为P( ),因为点P在渐近线y=
),因为点P在渐近线y= x上,所以
x上,所以 .渐近线y=
.渐近线y= 的倾斜角为30°.因此,两条渐近线的夹角为60°.
的倾斜角为30°.因此,两条渐近线的夹角为60°. 16.30 第一类:已知PA、PD、PO中的任意两条,可编
16.30 第一类:已知PA、PD、PO中的任意两条,可编 =3种
=3种 ×
× ×
× 得 sin(B-45°)=
得 sin(B-45°)= .
. 得AB=BC×
得AB=BC× =
= ………9分
………9分
 …10分
…10分 ……………………………………2分
……………………………………2分 表示电路不通,所以 D=
表示电路不通,所以 D= (或D=
(或D= 或D=
或D= )(只要求写出一种情况)
………………………………………4分
)(只要求写出一种情况)
………………………………………4分 (或
(或 或
或 ),(只要求写出一种情况)
………………………………………6分
),(只要求写出一种情况)
………………………………………6分 )P(
)P( )=0.9×(1-0.2×0.3)=0.846.
)=0.9×(1-0.2×0.3)=0.846. 设AC与MN的交点为O,连结OE,则OE∥PC,
设AC与MN的交点为O,连结OE,则OE∥PC, ,
,
 ,
, .
. . ……………………………12分
. ……………………………12分 P(0,0,2
P(0,0,2 (-1,-3,
(-1,-3, (-2,2,-2
(-2,2,-2 =
=  .
. 是平面BCFE的一个法向量,
是平面BCFE的一个法向量,  (0,-2,-2
(0,-2,-2 =(-4,4,0). ……………………………………………………………9分
=(-4,4,0). ……………………………………………………………9分 =
=  = eax(alnx+
= eax(alnx+ ,
, ,∴
,∴ ,
, +∞时,f¢(x)<0,与f(x)在(0,+∞)上递增矛盾;
+∞时,f¢(x)<0,与f(x)在(0,+∞)上递增矛盾; .
. 时,g’(x)<0,当x>
时,g’(x)<0,当x> x[2x2-3(a+1)x+6a]有一个根是0, …………………… 7分
x[2x2-3(a+1)x+6a]有一个根是0, …………………… 7分 且a≠0. ……………11分
且a≠0. ……………11分 +1)an得Sn-1=2-(
+1)an得Sn-1=2-( +1)an-1,
+1)an-1, =
= (n≥2),
……………………………3分
(n≥2),
……………………………3分 =
= . ……………………………5分
. ……………………………5分 ,
……………………………6分
,
……………………………6分 ,
, =2(1-
=2(1- )=
)= .
. =
= ,问题转化为比较
,问题转化为比较 与
与 的大小.
的大小. ,当n≥3时, f(n+1)-f(n)>0,
,当n≥3时, f(n+1)-f(n)>0,