机密★启用前 【考试时间:5月5日 15:00~17:00】
昆明市2008~2009学年高三复习适应性检测
理科数学试卷
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。第Ⅰ卷1至3页,第Ⅱ卷4至6页. 考试结束后,将本试卷和答题卡一并交回。满分150分,考试用时120分钟。
第Ⅰ卷(选择题 ,共60分)
注意事项:
1. 答题前,考生务必用黑色碳素笔将自己的姓名、考号在答题卡上填写清楚,并认真核准条形码上的考号、姓名,在规定的位置贴好条形码。
2. 每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑。如需改动,用橡皮擦擦干净后,再选涂其它答案标号。答在试卷上的答案无效。
参考公式:
如果事件A、B互斥,那么 球的表面积公式


如果事件A、B相互独立,那么 其中R表示球的半径
 球的体积公式
球的体积公式
如果事件A在一次试验中发生的概率是P,那么 
n次独立重复试验中恰好发生k次的概率 其中R表示球的半径

一.选择题:本大题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。
(1)函数 的定义域是
的定义域是
(A)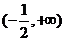 (B)
(B) (C)
(C) (D)
(D)
(2)若复数 满足
满足 ,则在复平面内
,则在复平面内 所对应的点在
所对应的点在
(A)第一象限 (B)第二象限 (C)第三象限 (D)第四象限
(3)函数 的最小正周期是
的最小正周期是
(A) (B)
(B) (C)
(C) (D)
(D)
(4)焦点在 轴上,中心在原点的椭圆上一点到两焦点的距离之和为
轴上,中心在原点的椭圆上一点到两焦点的距离之和为 ,若该椭圆的离心率为
,若该椭圆的离心率为 ,则椭圆的方程是
,则椭圆的方程是
(A) (B)
(B) (C)
(C) (D)
(D)
 (5)若把汽车的行驶路程
(5)若把汽车的行驶路程 看作时间
看作时间 的函数,下图是函数
的函数,下图是函数 在
在 上的图像,则在
上的图像,则在 上汽车的行驶过程为
上汽车的行驶过程为
(A)先加速行驶、然后匀速行驶、再加速行驶
(B)先减速行驶、然后匀速行驶、再加速行驶
(C)先加速行驶、然后匀速行驶、再减速行驶
(D)先减速行驶、然后匀速行驶、再减速行驶
(6)若
 +
+ +…+
+…+ +
+ +
+ ,则
,则 等于
等于
(A) (B)
(B) (C)
(C) (D)
(D)
(7)在公差不为零的等差数列 中,
中, ,
, 、
、 、
、 成等比数列.若
成等比数列.若 是数列
是数列 的前
的前 项和,则
项和,则 是
是
(A) (B)
(B) (C)
(C) (D)
(D)
(8)2名医生和4名护士分配到两所社区医院进行“健康普查”活动,每所医院分配1名医生和2名护士的不同分配方案共有
(A)6种 (B)8种 (C)12种 (D)24种
(9)若函数 存在反函数,则
存在反函数,则 的取值范围是
的取值范围是
(A)
(B)
(B) (C)
(C) (D)
(D)
(10)在正 中,
中, 为
为 边上的高,
边上的高, 为边
为边 的中点.若将
的中点.若将 沿
沿 翻折成直二面角
翻折成直二面角 ,则异面直
,则异面直
|
 (B)
(B) (C)
(C) (D)
(D)
 ,直线
,直线
 ,
, 是坐标原点,
是坐标原点, 是直线
是直线 上的一点,若
上的一点,若 ,则
,则 的最小值是
的最小值是
(B)
(B) (C)
(C) (D)
(D)
 的方程组
的方程组 有四组不同实数解的一个充分非必要条件是
有四组不同实数解的一个充分非必要条件是 (B)
(B) (C)
(C)  (D)
(D)
 的焦点坐标为
.
的焦点坐标为
. 的侧棱长与底面边长都相等,
的侧棱长与底面边长都相等, 在底面
在底面 的射影是
的射影是 的中点,则
的中点,则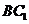 与侧面
与侧面 所成角的正切值等于
.
所成角的正切值等于
. 、
、 分别是角
分别是角 、
、 、
、 的对边,且
的对边,且 .
. ,且
,且 ,求
,求 的底面
的底面 是正方形,
是正方形, 面
面
 平面
平面 ;
; .
. 的中点,求二面角
的中点,求二面角 的大小.
的大小.
 ,至少有一项技术指标达标的概率为
,至少有一项技术指标达标的概率为 .检验规定两项技术指标都达标的新产品为合格品.
.检验规定两项技术指标都达标的新产品为合格品. ;
; 、
、 ,
, 为双曲线右支上一点,且
为双曲线右支上一点,且 ,
, .
. ,过
,过 与
与 同向,
同向, 的面积为
的面积为 .若
.若 ,求
,求 的取值范围.
的取值范围. .
. 时,若函数
时,若函数 在
在 上为增函数,求实数
上为增函数,求实数 处的切线为
处的切线为 .若
.若 在
在 、
、 ,
, ,求
,求 的值.
的值. 中,
中,
 ,
, .
. ;
; ;
; 的前n项和,证明:
的前n项和,证明: .
. (14)
(14) (15)
(15)

 .
. ,
, ,
, ,
, ,
, .
. ,
, ,
, 为三角形的内角,
为三角形的内角, . ………………………5分
. ………………………5分 .
. 整理得
整理得 .
. .
. ,
, 得
得
 .
. ,
, ,
, . ………………………………………………10分
. ………………………………………………10分 (18)(本小题满分12分)
(18)(本小题满分12分) 面
面 ,
, 面
面 .
. .
. ,
, 面
面 ,
, ,
,
 平面
平面 .
. ,则
,则 ,在
,在 中,
中, .
. 、
、 、
、 、
、 、
、 、
、 .
. ∵
∵ 为
为 的中点,
的中点, ,
, .
. 是平面
是平面 的一个法向量.
的一个法向量. 则由
则由 可求得
可求得 .
. 是平面
是平面 ,
, ,即
,即 .
. 的大小为
的大小为 . ………………………………………12分
. ………………………………………12分 设
设 ,连接
,连接 ,过
,过 作
作 于
于 ,
, ,由(Ⅰ)知
,由(Ⅰ)知 面
面 .
. ,
, .
. 为二面角
为二面角 的平面角.
的平面角. 中,
中, ,
, ,
, .
. ,
, .
. .
. 、
、 、
、 .
. …………2分
…………2分 .
. . …………6分
. …………6分 件,获得奖金
件,获得奖金 元,则
元,则 . ………………8分
. ………………8分 ~
~ ,
, ,
………………10分
,
………………10分 .
. ,
, ,
, ,
, 及勾股定理得
及勾股定理得 ,
, .
. .
………………………………………5分
.
………………………………………5分 ,
,
 ,故双曲线的两渐近线方程为
,故双曲线的两渐近线方程为 .
. 过
过 , 且
, 且 与
与 同向,故设
同向,故设 ,
,
 的面积
的面积 ,所以
,所以 .
. 轴的交点为
轴的交点为 .
. 交于点
交于点 交于点
交于点 得
得 ;由
;由 得
得 .
. ,
,
 ,
, ,
, .
. 的取值范围是
的取值范围是 . …………………………12分
. …………………………12分 ,
, .
. 在
在 上为增函数,
上为增函数, 在
在 在
在 ,
, 时取等号,而
时取等号,而 ,
, 的最小值为
的最小值为 .
………………………………………6分
.
………………………………………6分 为奇函数,
为奇函数, ,
,  , ………………………………7分
, ………………………………7分 .
. ,其中
,其中 ,
, ……………………8分
……………………8分 ,
, .
. ,
, ,
, ,
, ,
, 或
或 ,由题意知,
,由题意知,
 .
. ,
, ,
, .
………………………………………12分
.
………………………………………12分 ,
,
 得
得 ,
, . …………………………3分
. …………………………3分
 , ………………………4分
, ………………………4分 时,
时, 时,
时, 成立,
成立,
 时,等式也成立.
时,等式也成立. 成立. ……………8分
成立. ……………8分 ,则
,则 ,
, 在
在 上是增函数.
上是增函数. .
. .
. ,
, .
. =
= .…………12分
.…………12分