四川省南充市08-09学年高二教学质量监测
数学试卷(理科)
(考试时间100分钟 满分100分)
说明:1.本试卷分第Ⅰ卷(选择题、填空题)1至2页和第Ⅱ卷(答题卷)3至6页两部分。
2.考生务必用蓝黑墨水或圆珠笔作答。并将第Ⅰ卷的答案填在第Ⅱ卷指定位置。
3.只交答题卷
第Ⅰ卷(选择题、填空题卷)
一、选择题(本大题共10个小题,每小题4分,满分40分;在每小题给出的四个选项中,只有一项符合题目要求。请将答案填在答题栏内)
1.直线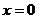 的斜率为( )
的斜率为( )
A.0
B.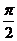
C.1 D.不存在
2.已知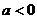 ,
,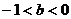 ,则有( )
,则有( )
A.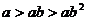 B.
B.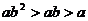
C.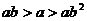 D.
D.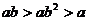
 3.直线
3.直线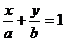 的一个方向向量是( )
的一个方向向量是( )
A.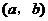 B.
B.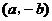
 C.
C. D.
D.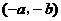
 4.直线
4.直线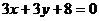 到直线
到直线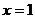 的角等于( )
的角等于( )
 A.
A.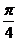 B.
B.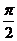
 C.
C.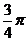 D.
D.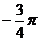
 5.已知
5.已知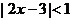 ,且
,且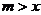 恒成立,则有( )
恒成立,则有( )
 A.
A.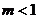 B.
B.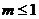
 C.
C.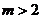 D.
D.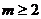
 6.圆
6.圆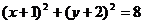 上到直线
上到直线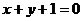 的距离等于
的距离等于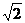 的点共有( )
的点共有( )
 A.1
B.2
A.1
B.2
 C.3
D.4
C.3
D.4

 7.不等式
7.不等式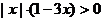 的解集为( )
的解集为( )
 A.
A.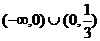 B.
B.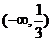
 C.
C.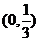 D.
D.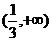
 8.已知弦
8.已知弦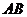 过抛物线
过抛物线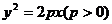 的焦点,则以
的焦点,则以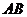 为直径的圆与抛物线的准线的位置关系是( )
为直径的圆与抛物线的准线的位置关系是( )
 A.相切
B.相离
A.相切
B.相离
 C.相交
D.与抛物线的
C.相交
D.与抛物线的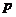 值有关
值有关
 9.双曲线的焦点是
9.双曲线的焦点是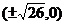 ,渐近线方程是
,渐近线方程是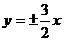 ,则它的两条准线间的距离是( )
,则它的两条准线间的距离是( )
 A.
A.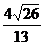 B.
B.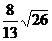
 C.
C.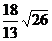 D.
D.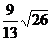


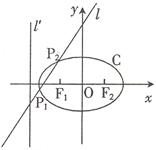
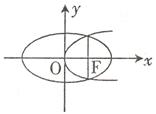 10.如图,椭圆
10.如图,椭圆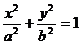
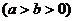 的右焦点
的右焦点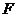 与
与
 抛物线
抛物线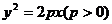 的焦点重合,且椭圆与抛物
的焦点重合,且椭圆与抛物
 线公共点的连线段过点
线公共点的连线段过点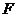 ,则椭圆的离心率
,则椭圆的离心率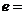 ( )
( )
 A.
A.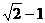 B.
B.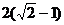
 C.
C.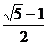 D.
D.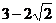
 二、填空题(本大题共4个小题,每个小题4分,满分16分;请将答案填在第Ⅱ卷答题栏的横线上)
二、填空题(本大题共4个小题,每个小题4分,满分16分;请将答案填在第Ⅱ卷答题栏的横线上)
 11.椭圆
11.椭圆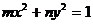
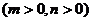 的焦点在
的焦点在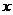 轴上,则
轴上,则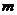
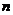 (用>,<填空=)。
(用>,<填空=)。
 12.不等式组
12.不等式组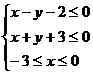 表示的平面区域的面积等于
。
表示的平面区域的面积等于
。
 13.已知
13.已知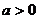 ,
,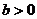 ,且
,且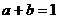 ,则
,则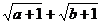 的最大值为
。
的最大值为
。
 14.直线
14.直线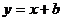 与曲线
与曲线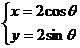 (参数
(参数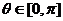 ),有两个公共点,则实数
),有两个公共点,则实数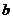 的范围是
。
的范围是
。

 第Ⅱ卷(答题栏)
第Ⅱ卷(答题栏)
题号
一
二
三
总分
15
16
17
18
19
得分
得分
评卷人
题号
1
2
3
4
5
6
7
8
9
10
答案
得分
评卷人
二、填空题答题栏 11 12
 13
14
13
14

得分
评卷人
 三、解答题(本大题共5个小题,满分44分,解答题应写出必要的解答过程或演算步骤)
三、解答题(本大题共5个小题,满分44分,解答题应写出必要的解答过程或演算步骤)
 15.(本题满分12分)完成下列各小题:
15.(本题满分12分)完成下列各小题:

①
 解不等式:
解不等式: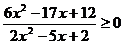 ;
;
②
 已知直线
已知直线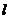 过点
过点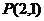 且和直线
且和直线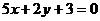 垂直,求直线
垂直,求直线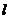 的方程;
的方程;
得分
评卷人
 16.(本题满分7分)
16.(本题满分7分)

 已知
已知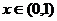 ,
,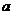 ,
,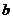 为正常数,求
为正常数,求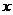 为何值时,函数
为何值时,函数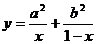 取得最小值,并求出该最小值。
取得最小值,并求出该最小值。

得分
评卷人
 17.(本题满分7分)
17.(本题满分7分)

 直线
直线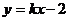 交抛物线
交抛物线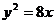 于
于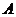 、
、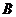 两点,若线段
两点,若线段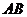 中点的横坐标等于2,求弦
中点的横坐标等于2,求弦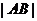 长。
长。

得分
评卷人
 18.(本题满分8分)
18.(本题满分8分)

 已知双曲线的中心在原点,焦点
已知双曲线的中心在原点,焦点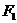 、
、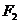 在坐标轴上,离心率
在坐标轴上,离心率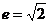 且过点
且过点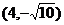 。
。
①
 求此双曲线标准方程;
求此双曲线标准方程;
②
 若直线
若直线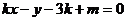 (其中
(其中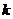 为参数)所过的定点
为参数)所过的定点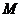 恰在双曲线上,求证:
恰在双曲线上,求证: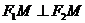 。
。

得分
评卷人

 19.(本题满分10分)
19.(本题满分10分)

 如图:
如图: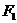 、
、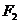 为椭圆
为椭圆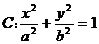
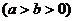 的
的
 左、右焦点,直线
左、右焦点,直线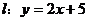 与椭圆
与椭圆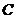 交于两点
交于两点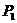 、
、

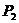 ,已知椭圆中心
,已知椭圆中心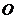 点关于
点关于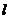 的对称点恰好落在椭圆
的对称点恰好落在椭圆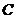 的
的
 左准线
左准线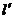 上。
上。
①

 求准线
求准线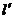 的方程;
的方程;
②
 已知
已知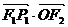 、
、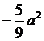 、
、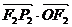 成等差数列,
成等差数列,
 求椭圆
求椭圆 的方程。
的方程。

四川省南充市08-09学年高二教学质量监测
一、选择题(4′×10=40分)
题号
1
2
3
4
5
6
7
8
9
10
答案
D
D
B
C
D
C
A
A
B
A
三、填空题(4′×4=16分)
11. 12.
12. 13.
13. 14.
14.
三、解答题(共44分)
15.①解:原不等式可化为: ………………………2′
………………………2′
 作根轴图:
作根轴图:
………………………4′
可得原不等式的解集为: ………………………6′
………………………6′
②解:直线 的斜率
的斜率 ………………………2′
………………………2′
∵直线 与该直线垂直
与该直线垂直
∴ ………………………4′
………………………4′
则 的方程为:
的方程为: ………………………5′
………………………5′
即 为所求………………………6′
为所求………………………6′
 16.解:∵
16.解:∵ ∴
∴ ,
, 且
且 ………………………1′
………………………1′
于是 ………………………3′
………………………3′
 ………………………4′
………………………4′
 ………………………5′
………………………5′

当且仅当: 即
即 ………………………6′
………………………6′
 时,
时, ………………………7′
………………………7′
17.解:将 代入
代入 中变形整理得:
中变形整理得:
 ………………………2′
………………………2′
首先
 且
且 ………………………3′
………………………3′
设

由题意得:
解得: 或
或 (舍去)………………………5′
(舍去)………………………5′
由弦长公式得: ………………………7′
………………………7′
18.解①设双曲线的实半轴,虚半轴分别为 ,
,

由题得: ∴
∴ ………………………1′
………………………1′
于是可设双曲线方程为: ………………………2′
………………………2′
将点 代入可得:
代入可得: ,
,
∴该双曲线的方程为: ………………………4′
………………………4′
②直线方程可化为: ,
,
则它所过定点 代入双曲线方程:
代入双曲线方程: 得:
得:

∴ ………………………6′
………………………6′
又由 得
得 ,
,
∴ ,
, 或
或 ,
, …………7′
…………7′
∴
∴ ……………………8′
……………………8′
19.解:①设中心 关于
关于 的对称点为
的对称点为 ,
,
则 解得:
解得:
∴ ,又点
,又点 在左准线
在左准线 上,
上, 轴
轴
∴ 的方程为:
的方程为: ……………………4′
……………………4′
②设 、
、 、
、 、
、
∵ 、
、 、
、 成等差数列,
成等差数列,
∴ ,
,
即:
亦:
∴ ……………………6′
……………………6′
 ∴
∴
由 得
得 ……………………8′
……………………8′
∴ , ∴
, ∴
又由 代入上式得:
代入上式得:
∴ ,
, ∴
∴ ……………………9′
……………………9′
∴ ,
, ,
,
∴椭圆的方程为: