2009云南省曲靖一中高考冲刺卷文科数学 (二)
(二)
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,满分150分,考试时间120分钟。
第Ⅰ卷(选择题,共60分)
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只
有一项是符合题目要求的.
1.若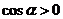 ,且
,且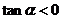 ,则
,则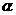 是
是
A.第一象限角 B.第二象限角
C.第三象限角 D.第四象限角
2.设集合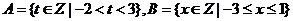 ,则
,则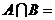

A.{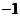 ,0} B.{0,1,2}
,0} B.{0,1,2}
C.{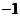 ,0,1} D.{
,0,1} D.{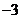 ,
,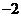 ,0,1,2}
,0,1,2}
3.原点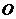 到直线
到直线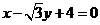 的距离等于
的距离等于
A.1 B.
4.函数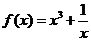 的图象
的图象
A.关于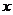 轴对称 B.关于
轴对称 B.关于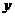 轴对称
轴对称
C.关于直线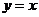 对称 D.关于坐标原点对称
对称 D.关于坐标原点对称
5.若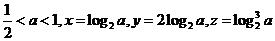 ,则
,则
A.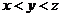 B.
B.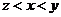

C.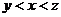 D.
D.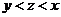

6.已知实数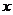 、
、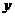 同时满足三个条件:①
同时满足三个条件:①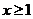 ;②
;② 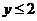 ;③
;③ 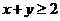 ,则
,则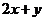 的
的
最小值等于
A.3 B.4 C.5
D.6
7.曲线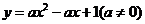 在点(0,1)处的切线与直线
在点(0,1)处的切线与直线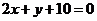 垂直,则
垂直,则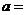

A.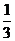 B.
B.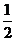 C.
C.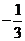 D.
D.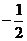

8.正四棱锥的底面边长等于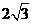 ,侧面与底面成60°的二面角,此四棱锥体积为
,侧面与底面成60°的二面角,此四棱锥体积为
A.9 B.12 C.15 D.18
9.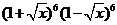 展开式中
展开式中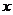 的系数是
的系数是
A.6 B.15 C.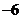 D.
D.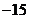

10.函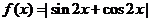 的值域是
的值域是
A.[0,1] B.[0,2]
C.[0,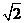 ] D.[1,
] D.[1,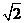 ]
]
11. 曲线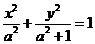 的离心率的取值范围是
的离心率的取值范围是
A.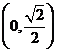 B.
B.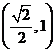 C.
C.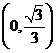 D.(0,1)
D.(0,1)
12.正四面体的内切球与外接球的半径的比等于
A.1:3 B.1:2 
C.2:3 D.3:5

第Ⅱ卷(非选择题,共90分)
二、填空题:本大题共4小题,每小题5分,共20分.把答案填在题中横线上.
13.已知向量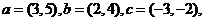
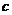 与
与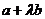 共线,则
共线,则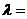 .
.
14.从5名男运动员、4名女运动员中选四人参加4×100米接力赛跑,则选到的四名运动员
既有男运动员又有女运动员的不同选法共有
种(用数字作答).
15.曲线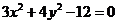 的过焦点且倾角是135°的弦的长度等于
.
的过焦点且倾角是135°的弦的长度等于
.
16.请写出一个三棱锥是正三棱锥的两个充要条件:
充要条件①
;
充要条件②
;


三、解答题:本大题共6小题.共70分,解答应写出文字说明、证明过程或演算步骤.
17.(本小题满分12分)
在等差数列 中,
中,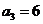 ,
,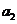 、
、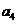 、
、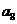 成等比数列,求数列
成等比数列,求数列 的前
的前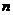 项和.
项和.






18.(本小题满分10分)
在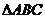 中,
中,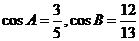 ,且
,且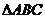 的面积
的面积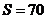 ,求
,求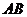 的长.
的长.






19.(本小题满分12分)
甲、乙、丙三人进行射击比赛,在一轮比赛中,甲、乙丙各射击一发子弹,根据以往统计资料知,甲击中9环、10环的概率为0.3、0.2,乙中击中9环、10环的概率0.4、0.3,丙击中9环、10环的概率是0.6、0.4,设甲、乙、丙射击相互独立,求:
(1)丙击中的环数不超过甲击中的环数的概率;
(2)求在一轮比赛中,甲、乙击中的环数都没有超过丙击中的环数的概率.






20.(本小题满分12分)
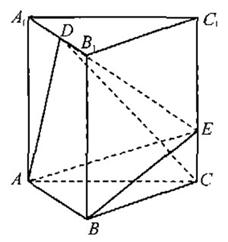 在正三棱柱
在正三棱柱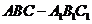 中,
中,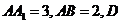 是
是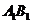 的中点,
的中点,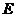 在线段
在线段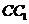 上且
上且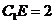 .
.
(1)证明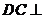 面
面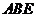 ;
;
(2)求二面角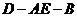 的大小.
的大小.











21.(本小题满分12分)
函数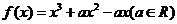 .
.
(1)若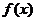 在
在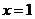 处取得极植,求
处取得极植,求 的值;
的值;
(2)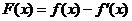 在区间
在区间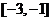 上是增函数,求
上是增函数,求 的取值范围.
的取值范围.





22.(本小题满分12分)
点 是椭圆短轴的一个端点,
是椭圆短轴的一个端点,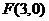 是椭圆的一个焦点,直线
是椭圆的一个焦点,直线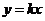 与线段
与线段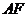 相交于点
相交于点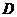 (
(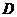 与
与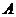 、
、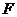 不重合),直线
不重合),直线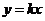 与椭圆相交于
与椭圆相交于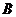 、
、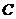 两点.
两点.
(1)若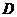 是
是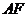 的一个三等分点,求
的一个三等分点,求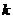 的值;
的值;
(2)求四边形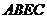 面积的最大值.
面积的最大值.
一、
1.D 2.C 3.B 4.D 5.C 6.A 7.D 8.B 9.C 10.C
11.D 12.A
【解析】
5.解: ,则
,则 .
.
6.解:线性规划问题可先作出可行域(略),设 ,则
,则 ,可知在点(1,1)处
,可知在点(1,1)处 取最小值,
取最小值, .
.
7.解: ,由条件知曲线在点(0,1)处的切线斜率为
,由条件知曲线在点(0,1)处的切线斜率为 ,则
,则 .
.
8.解:如图

正四棱锥 中,取
中,取 中点
中点 ,连接
,连接 、
、 ,易知
,易知 就是侧面与底面所成角,
就是侧面与底面所成角, 面
面 ,则
,则 .
.
9.解: ,展开式中含
,展开式中含 的项是
的项是 ,其系数是
,其系数是 .
.
10.解: ,其值域是
,其值域是 .
.
11.解: ,设离心率为
,设离心率为 ,则
,则 ,由
,由 知
知 .
.
12.解:如图

正四面体 中,
中, 是
是 中心,连
中心,连 ,此四面体内切球与外接球具有共同球心
,此四面体内切球与外接球具有共同球心 ,
, 必在
必在 上,并且
上,并且 等于内切球半径,
等于内切球半径, 等于外接球半径.记
等于外接球半径.记 面积为
面积为 ,则
,则
 ,从而
,从而

 .
.
二、填空题
13. .
.
解: ,
, 与
与 共线
共线 .
.
14.120种.
解:按要求分类相加,共有 种,或使用间接法:
种,或使用间接法: 种.
种.
15. .
.
解:曲线 ①,化作标准形式为
①,化作标准形式为 ,表示椭圆,由于对称性,取焦点
,表示椭圆,由于对称性,取焦点 ,过
,过 且倾角是135°的弦所在直线方程为:
且倾角是135°的弦所在直线方程为: ,即
,即 ②,联立式①与式②消去
②,联立式①与式②消去 得:
得:

 ,由弦长公式得:
,由弦长公式得: .
.
16.充要条件①:底面是正三角形,顶点在底面的射影恰是底面的中心.
充要条件②:底面是正三角形,且三条侧棱长相等,
再如:底面是正三角形,且三个侧面与底面所成角相等;底面是正三角形,且三条侧棱与底面所成角相等;三条侧棱长相等,且三个侧面与底面所成角相等;三个侧面与底面所成角相等,三个侧面两两所成二面角相等.
三、解答题
17.解:设等差数列 的公差为
的公差为 、
、 、
、 成等比数列,即
成等比数列,即 ,
,
 ,得
,得 或
或 .
.
 时
时 是常数列,
是常数列, ,前
,前 项和
项和
 时,
时, 的前
的前 项和
项和

 或
或 .
.
18.解: ,则
,则 ,
, ,
, .
.
由正弦定理得:
 ,
,
 ,则
,则

 .
.
19.解:已知甲击中9环、10环的概率分别是0.3、0.2,则甲击中8环及其以下环数的概率是0.5;乙击中9环、10环的概率分别为0.4、0.3,则乙击中8环及其以下环数的概率是0.3;丙击中9环、10环的概率是0.6、0.4,0.6+0.4=1,则丙击中8环及其以下环数是不可能事件.
(1)记在一轮比赛中“丙击中的环数不超过甲击中的环数”为事件 ,
, 包括“丙击中9环且甲击中9或10环”、“丙击中10环且甲击中10环”两个互斥事件,则
包括“丙击中9环且甲击中9或10环”、“丙击中10环且甲击中10环”两个互斥事件,则
 .
.
(2)记在一轮比赛中,“甲击中的环数超过丙击中的环数”为事件 ,“乙击中的环数超过丙击中的环数”为事件
,“乙击中的环数超过丙击中的环数”为事件 ,则
,则 与
与 相互独立,且
相互独立,且 ,
, .
.
所以在一轮比赛中,甲、乙击中的环数都没有超过丙击中的环数的概率为:

 .
.
20.(1)证:已知 是正三棱柱,取
是正三棱柱,取 中点
中点 ,
, 中点
中点 ,连
,连 ,
, ,则
,则 、
、 、
、 两两垂直,以
两两垂直,以 、
、 、
、 为
为 、
、 、
、 轴建立空间直角坐标系,又已知
轴建立空间直角坐标系,又已知 ,
,
则
 .
.

 ,
, ,则
,则 ,又因
,又因 与
与 相交,故
相交,故 面
面 .
.
(2)解:由(1)知, 是面
是面 的一个法向量.
的一个法向量.
 ,设
,设 是面
是面 的一个法向量,则
的一个法向量,则 ①,
①, ②,取
②,取 ,联立式①与式②解得
,联立式①与式②解得 ,则
,则 .
.
二面角 是锐二面角,记其大小为
是锐二面角,记其大小为 .则
.则
 ,
,
二面角 的大小
的大小 ,亦可用传统方法解决(略).
,亦可用传统方法解决(略).
21.解: .
.
(1) 在
在 处取得极值,则
处取得极值,则 .
.
(2) ,
,

恒成立, 必有解.
必有解.
易知函数 图象(抛物线)对称轴方程是
图象(抛物线)对称轴方程是 .
.
 在
在 上是增函数,则
上是增函数,则 时恒有
时恒有 ,进而必有(数形结合)
,进而必有(数形结合)
 或
或 或
或 ,
,
故 的取值范围是:
的取值范围是: .
.
22.解:(1)已知 ,求得线段
,求得线段 的两个三等分点
的两个三等分点 、
、 ,直线
,直线 过
过 时,
时, ,直线
,直线 过
过 时,
时, ,故
,故 或
或 .
.

(2)已知 是椭圆短轴端点和焦点,易求得椭圆方程是:
是椭圆短轴端点和焦点,易求得椭圆方程是: ,
, 所在直线的方程为
所在直线的方程为 .
.
直线与 椭圆相交于
椭圆相交于 、
、 ,设
,设 ,
, ,由直线
,由直线 与线段
与线段 相交(交点不与
相交(交点不与 、
、 重合)知
重合)知 .
.
点 在椭圆上,则
在椭圆上,则 ,解得
,解得 到直线
到直线 的距离
的距离
 ,
,
点 到直线
到直线 的距离;
的距离;

设 ,则
,则 ,由
,由 知
知 ,则:
,则:

 ,
,
当 即
即 时,
时, 取到最大值
取到最大值 .
.
www.ks5u.com ,0与
,0与 中,0距
中,0距 更远,当
更远,当 且
且 时,
时,
 ,
,
 .
.
∴四边形 的面积
的面积 ,当
,当 时,
时, .
.