2009云南省曲靖一中高考冲刺卷理科数学(八)
 本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,满分150分,考试时间120分钟.
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,满分150分,考试时间120分钟.
第Ⅰ卷(选择题,共60分)
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只
有一项是符台题目要求的.
1.已知全集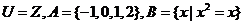 ,则
,则 为
为
A.{1,2} B.{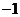 ,2) C.{
,2) C.{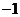 ,0) D.{
,0) D.{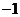 ,0,2)
,0,2)
2.已知复数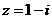 ,则
,则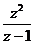 等于
等于
A.2 B.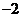 C.
C.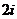 D.
D.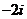

3.已知两个正数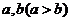 的等差中项为5,等比中项为4,则椭圆
的等差中项为5,等比中项为4,则椭圆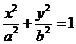 的离心率
的离心率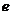

等于
A.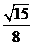 B.
B.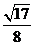 C.
C.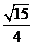 D.
D.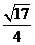

4.在平面直角坐标系中,已知向量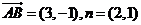 ,且
,且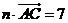 ,那么
,那么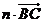 等
等
于
A.2或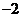 B.
B.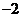 D.0
D.0
5.已知变量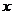 ,
,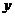 满足约束条件
满足约束条件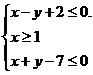 ,则
,则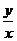 的取值范围是
的取值范围是
A. B.
B.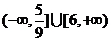

C.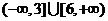 D.[3,6]
D.[3,6]
6.等差数列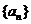 的前
的前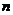 项和为
项和为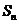 ,若
,若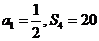 ,则
,则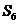 等于
等于
A.16 B.
7. 为矩形
为矩形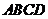 所在平面外一点,且
所在平面外一点,且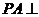 平面
平面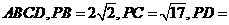

 ,则四棱锥
,则四棱锥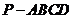 的体积等于
的体积等于
A.2 B.
8.设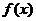 是定义在
是定义在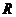 上的奇函数,若当
上的奇函数,若当 时,
时, ,则满足
,则满足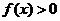 的
的
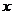 取值范围是
取值范围是
A.(0,1) B.(1,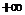 )
)
C.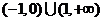 D.
D.

9.已知定点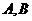 ,且
,且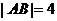 ,动点
,动点 满足
满足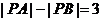 ,则
,则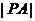 的最小值为
的最小值为
A. B.
B. C.
C.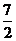 D.5
D.5
10.某一批油菜种子,如果每一粒种子发芽的概率是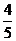 ,那么种下4粒种子恰有2粒发芽
,那么种下4粒种子恰有2粒发芽
的概率是
A.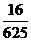 B.
B.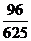 C.
C.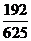 D.
D.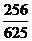

11.已知圆的方程为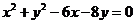 ,设该圆过点(3,5)的最长弦和最短弦分别为
,设该圆过点(3,5)的最长弦和最短弦分别为
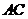 和
和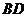 ,则四边形
,则四边形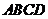 的面积为
的面积为
A.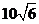 B.
B. C.
C.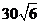 D.
D.

12.棱长为1的正方体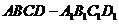 及其内部一动点
及其内部一动点 ,集合
,集合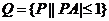 ,则
,则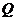

构成的几何体表面积为
A.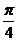 B.
B.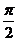 C.
C.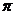 D.
D.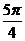


第Ⅱ卷(非选择题,共90分)
二、填空题:本大题共4小题。每小题5分,共20分,把答案填在题中横线上.
13.已知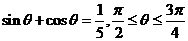 ,则
,则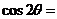 .
.
14.已知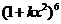 (
(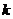 是正整数)的展开式中,
是正整数)的展开式中,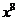 的系数小于120,则
的系数小于120,则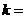 .
.
15.设函数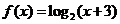 的图象为
的图象为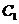 ,函数
,函数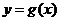 的图象为
的图象为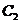 ,若
,若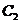 与
与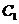 关于
关于
直线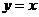 对称,则
对称,则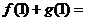 .
.
16.已知函数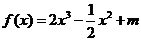 (
(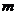 为常数)图象上
为常数)图象上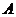 处的切线与直线
处的切线与直线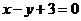 的
的
夹角为45°,则点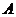 的横坐标为
.
的横坐标为
.
三、解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.(本小题满分10分)
已知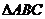 的面积为3,且满足
的面积为3,且满足 .设
.设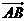 与
与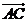 的夹角为
的夹角为 .
.
(1)求 的取值范围
的取值范围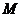 ;
;
(2)当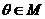 时,求函数
时,求函数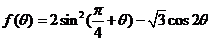 的最小值和最大值.
的最小值和最大值.

18.(本小题满分12分)
某商场准备在五一劳动节期间举行促销活动,根据市场调查,该商场决定从3种服装商品、2种家电商品、4种日用商品中,选出3种商品进行促销活动.
(1)试求选出的3种商品至少有一种日用商品的概率;
(2)商场对选出的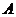 商品采用的促销方案是有奖销售,即在该商品现价的基础上将价格提高180元,同时允许顾客有3次抽奖的机会,若中奖,则每次中奖都可获得一定数额的奖金.假设顾客每次抽奖时获奖与否是等概率的.
商品采用的促销方案是有奖销售,即在该商品现价的基础上将价格提高180元,同时允许顾客有3次抽奖的机会,若中奖,则每次中奖都可获得一定数额的奖金.假设顾客每次抽奖时获奖与否是等概率的.
请问:商场应将中奖奖金数额最高定为多少元,才能使促销方案对自己有利?


 19.(本小题满分12分)
19.(本小题满分12分)
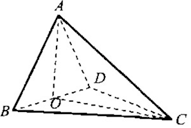
如图,四面体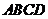 中,
中,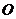 是
是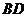 的中点,
的中点,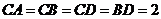 ,
,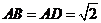 .
.
(1)求证: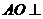 平面
平面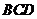 ;
;
(2)求异面直线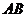 与
与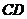 所成角的大小;
所成角的大小;
(3)求二面角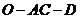 的大小.
的大小.



20.(本小题满分12分)
已知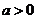 且
且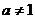 ,数列
,数列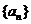 中,
中,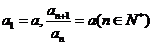 ,令
,令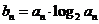 .
.
(1)若 ,求数列
,求数列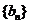 的前
的前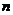 项和
项和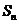 ;
;
(2)若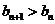 ,
,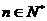 ,求
,求 的取值范围.
的取值范围.



21.(本小题满分12分)
已知椭圆 的左、右焦点分别为
的左、右焦点分别为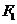 、
、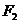 ,其中
,其中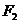 也是抛物线
也是抛物线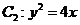 的焦点,
的焦点,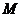 是
是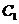 与
与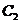 在第一象限的交点,且
在第一象限的交点,且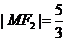 .
.
(1)求椭圆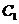 的方程;
的方程;
(2)已知菱形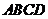 的顶点
的顶点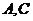 在椭圆
在椭圆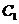 上,顶点
上,顶点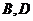 在直线
在直线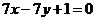 上,求直线
上,求直线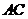 的方程.
的方程.



22.(本小题满分12分)
已知函数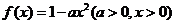 ,该函数图象在点
,该函数图象在点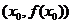 的切线为
的切线为 ,设切线
,设切线 交
交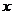 轴、
轴、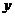 轴分别为
轴分别为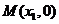 和
和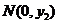 两点.
两点.
(1)将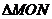 (
(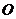 为坐标原点)的面积
为坐标原点)的面积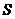 表示为
表示为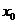 的函数
的函数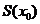 ;
;
(2)若函数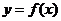 的图象与
的图象与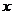 轴交于点
轴交于点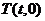 ,则
,则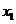 与
与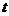 的大小关系如何?请证明你的结论;
的大小关系如何?请证明你的结论;
(3)若在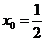 处,
处,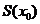 取的最小值,求此时
取的最小值,求此时 的值及
的值及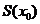 的最小值.
的最小值.


1.B 2.A 3.C 4.B 5.A 6.D 7.B 8.C 9.C 1
0.B 
11.B 12.D
1. .
.
2.

3. 是方程
是方程 的根,
的根, 或8,又
或8,又 ,
,
 .
.
4. .
.
5.画出可行域,如图, 可看为区域内的点与(0,0)连线的斜率,
可看为区域内的点与(0,0)连线的斜率, .
.
 .
.
6.
7.在 中,
中, ,在
,在 中,
中, ,
,
在 中,
中, ,在
,在 中,
中, ,
, .
.
8. 的图象如图所示
的图象如图所示
 的解集为
的解集为 .
.
9.由 知
知 点的轨迹是以
点的轨迹是以 ,
, 为焦点的双曲线一支.
为焦点的双曲线一支. ,
, .
.
10.由独立重复试验的概率 .
.
11.设 ,圆为
,圆为 最长弦
最长弦 为直径,最短弦
为直径,最短弦 的中点为
的中点为 ,
,

12.几何体的表面积是三个圆心角为 、半径为1的扇形面积与半径为1的球面积的
、半径为1的扇形面积与半径为1的球面积的 之和,即表面积为
之和,即表面积为 .
.
二、
13. 平方得
平方得
 .
.
14. 的系数
的系数
15.1. 与
与 互为反函数,
互为反函数,
令 ,
,
 .
.
16.0或  ,设
,设 点的横坐标为
点的横坐标为 点处的切线斜率为
点处的切线斜率为 ,由夹角公式得
,由夹角公式得 ,即
,即
若 ,得
,得 ,矛盾
,矛盾
若
 或
或 .
.
三、
17.(1) ,由
,由 ,得
,得 ,消去
,消去 得
得
 .
.
 .
.
(2)

 ,
,
 .
.
 时,
时, 的最大值为
的最大值为 时,
时, 的最大值为2.
的最大值为2.
18.(1)从3种服装商品、2种家电商品,4种日用商品中,选出3种商品,一共有 种不同的选法.选出的3种商品中,没有日用商品的选法有
种不同的选法.选出的3种商品中,没有日用商品的选法有 种。所以选出的3种商品至少有一种日用商品的概率为
种。所以选出的3种商品至少有一种日用商品的概率为 .
.
(2)假设商场将中奖奖金数额定为 元,则顾客在三欢抽奖中所获得的奖金总额是一个随机变量
元,则顾客在三欢抽奖中所获得的奖金总额是一个随机变量 ,其所有可能的取值为
,其所有可能的取值为




于是顾客在三次抽奖中所获得的奖金总额的期望值是
 .
.
要使促销方案对商场有利,因此应有 ,
, .
.
故商场应将中奖奖金数额最高定为120元.才能使促销方案对自己有利.
19.(1)证明: .
.
连接 .
.
 ,又
,又

即
 平面
平面 .
.
(2)方法1 取 的中点
的中点 ,
, 的中点
的中点 ,
, 为
为 的中点,
的中点, 或其补角是
或其补角是 与
与 所成的角.
所成的角.
∴连接 是
是 斜边
斜边 上的中线,
上的中线, ,
,
 .
.
在 中,由余弦定理得
中,由余弦定理得 ,
,
∴直线 与
与 所成的角为
所成的角为 .
.
(3)方法l
 平面
平面 ,过
,过 作
作 于
于 ,连接
,连接 ,
,
 是
是 在平面
在平面 上的射影,由三垂线定理得
上的射影,由三垂线定理得 .
.
 是二面角
是二面角 的平面角,
的平面角,
 ,又
,又 .
.
在 中,
中, ,
, .
.
∴二面角 为
为 .
.
(2)方法2
建立空间直角坐标系 .
.
则

 .
.
 .
.
∴直线 与
与 所成的角为
所成的角为 .
.
(3)方法2
在坐标系中,平面 的法向量
的法向量 .
.
设平面 的法向量
的法向量 ,则
,则 ,
,
求得 ,
,
∴二面角 为
为 .
.
20. 是首项为
是首项为 、公比为
、公比为 的等比数列,
的等比数列,

(1)当 时,
时,



两式相减得

 .
.
(2)
当 时,
时, ,
, ,对
,对 ,
, ,而
,而 ,
,
 时,
时, 成立,即
成立,即 .
.
当 时,
时, .
.
 对
对 递增,
递增, 时,
时,
 时,
时, 对
对 成立,即
成立,即 ,
,
综上得, 的取值范围是
的取值范围是 .
.
21.(1)设 .
.
由抛物线定义, ,
,
 .
.
 在
在 上,
上, ,又
,又

 或
或 舍去.
舍去.

∴椭圆 的方程为
的方程为 .
.
(2)∵直线 的方程为
的方程为 为菱形,
为菱形,
 ,设直线
,设直线 的方程为
的方程为
 、
、 在椭圆
在椭圆 上,
上,
 .
.
设 ,则
,则 .
.
 .
.
 的中点坐标为
的中点坐标为 ,由
,由 为菱形可知,点
为菱形可知,点 在直线
在直线 上,
上,


∴直线 的方程为
的方程为 ,即
,即 .
.
22.(1) ,切线
,切线 的议程为
的议程为 ,即
,即 .
.
令 得
得 ,令
,令 得
得 ,
,
 ,
,
 .
.

(2)由 及
及 得
得 ,即
,即 .
.
于是
当且仅当 ,即
,即 时,等号成立.
时,等号成立.
 时,
时, 时,
时, .
.
(3)
由 得
得
当 ,即
,即 时,
时, ,
,
当 ,即
,即 时,
时,
 时,
时, 取得最小值,最小值为
取得最小值,最小值为 .
.
由 ,得
,得 ,此时,
,此时, 最小值为
最小值为 .
.