2009年云南省曲靖一中高考冲刺卷理科数学 (六)
(六)
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,满分150分,考试时间120分钟。
第Ⅰ卷(选择题,共60分)
一、选择题:本大题共12小题。每小题5分,共60分.在每小题给出的四个选项中,只
有一项是符合题目要求的.
1.复数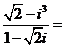

A.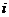 B.
B.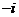 C.
C.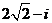 D.
D.

2.设集合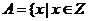 ,且
,且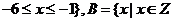 ,且
,且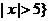 ,则
,则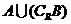 中的
中的
元素个数是
A.9 B.
3.若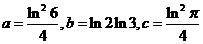 ,则
,则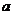 ,
,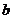 ,
,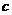 的大小关系是
的大小关系是
A.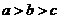 B.
B.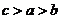 C.
C.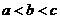 D.
D.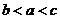

4.设变量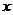 ,
,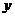 满足约束条件
满足约束条件 ,则目标函数
,则目标函数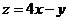 的最大值为
的最大值为
A.5 B.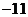

5.据统计,甲、乙两人投篮的命中率分别为0.5、0.4,若甲、乙两人各投一次,则有人
投中的概率是
A.0.2 B.0.3 C.0.7 D.0.8
6.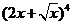 展开式中含
展开式中含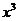 的系数是
的系数是
A.6 B.12 C.24 D.48
7.设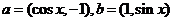 ,则
,则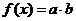 在
在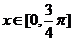 上的最大值与最小值分别
上的最大值与最小值分别
是
A.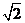 与
与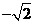 B.1与
B.1与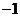 C.
C.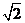 与
与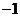 D.1与
D.1与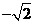

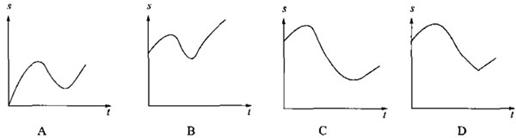
8.某地区的经济在某段时间内经历了高涨、保持、下滑、危机、萧条、复苏几个阶段,则
该地区的经济量 随时间
随时间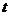 的变化图象大致可能是
的变化图象大致可能是

9.已知双曲线 的一条准线与抛物线
的一条准线与抛物线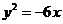 的准线重合,则该双曲线
的准线重合,则该双曲线 
的离心率为
A.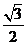 B.
B.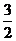 C.
C.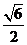 D.
D.

10.已知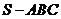 是正四面体,
是正四面体,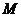 为
为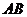 之中点,则
之中点,则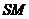 与
与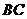 所成的角为
所成的角为
A. B.
B.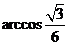 C.
C.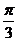 D.
D.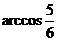

11.直线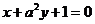 与直线
与直线 互相垂直,
互相垂直,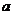 、
、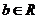 且
且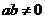 ,则
,则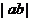

的最小值为
A.1 B.2 C.3 D.4
12.正四面体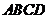 的外接球的体积为
的外接球的体积为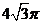 ,则点
,则点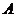 到平面
到平面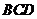 的距离为
的距离为
A.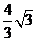 B.
B.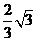 C.
C.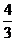 D.
D.


第Ⅱ卷(非选择题,共90分)
二、填空题:本大题共4小题,每小题5分。共20分.把答案填在题中横线上.
13.若 则
则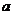 在
在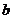 上的投影是
.
上的投影是
.
14.设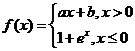 ,若
,若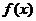 在
在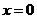 处连续,则
处连续,则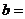 .
.
15.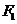 、
、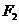 是椭圆
是椭圆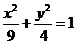 的两个焦点,
的两个焦点,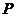 为椭圆上一动点,若
为椭圆上一动点,若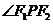 为钝角,则点
为钝角,则点
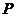 的横坐标的范围是
.
的横坐标的范围是
.
16.设有四个条件:
① 平面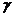 与平面
与平面 ,
,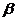 所成的锐二面角相等;
所成的锐二面角相等;
② 直线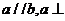 平面
平面 平面
平面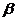 ;
;
③ 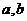 是异面直线,
是异面直线,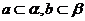 ,且
,且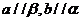 ;
;
④ 平面 内距离为
内距离为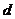 的两条平行直线在平面
的两条平行直线在平面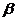 内的射影仍为两条距离为
内的射影仍为两条距离为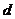 的平行直线.
的平行直线.
其中能推出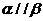 的条件有
.
的条件有
.
三、解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.
17.(本小题满分10分)
已知向量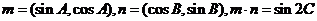 ,且
,且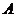 、
、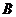 、
、 分别为
分别为 的三边
的三边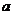 ,
,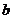 ,
,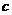 所对的角.
所对的角.
(1)求角 的大小;
的大小;
(2)若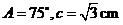 ,求
,求 的面积.
的面积.
18.(本小题满分12分)
甲、乙等四名医务志愿者被随机地分到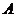 、
、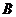 、
、 三个不同的地震灾区服务,每个灾区至少有一名志愿者.
三个不同的地震灾区服务,每个灾区至少有一名志愿者.
(1)求甲、乙两人同时参加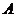 灾区服务的概率;
灾区服务的概率;
(2)求甲、乙两人在同一个灾区服务的概率;
(3)设随机变量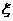 为这四名志愿者中参加
为这四名志愿者中参加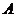 灾区服务的人数,求
灾区服务的人数,求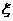 的分布列.
的分布列.
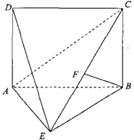



19.(本小题满分12分)
如图,直二面角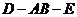 中,四边形
中,四边形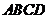 是边长为2的正方形,
是边长为2的正方形,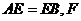 为CE上的点,且
为CE上的点,且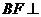 平面
平面 .
.
(1)求证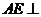 平面
平面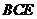 ;
;
(2)求二面角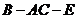 的大小.
的大小.

20.(本小题满分12分)
已知数列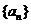 、
、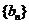 满足
满足 ,且
,且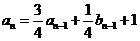 ,
,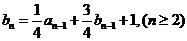

(1)令 ,求数列
,求数列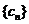 的通项公式;
的通项公式;
(2)求数列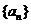 的通项公式及前
的通项公式及前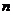 项和公式
项和公式 .
.

21.(本小题满分12分)
已知曲线 上任意一点到椭圆
上任意一点到椭圆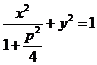 (
(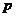 为正常数)右焦点
为正常数)右焦点 的距离等于到定直线
的距离等于到定直线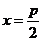 的距离.
的距离.
(1)求曲线 的方程;
的方程;
(2)若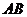 是曲线
是曲线 上过点
上过点 的直线,且
的直线,且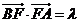 ,试证
,试证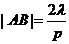 .
.

22.(本小题满分12分)
设函数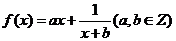 曲线
曲线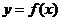 在点
在点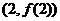 处的切线方程为
处的切线方程为 .
.
(1)求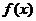 的解析式;
的解析式;
(2)证明:函数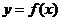 的图象是一个中心对称图形,并求其对称中心;
的图象是一个中心对称图形,并求其对称中心;
(3)证明:曲线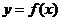 任一点的切线与直线
任一点的切线与直线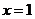 和直线
和直线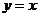 所围三角形的面积为定值,并求出此定值.
所围三角形的面积为定值,并求出此定值.
1.A 2.C 3.B 4.A 5.C 6.C 7.D 8.C 9.D 10.B 
1l.B 12.A
1.解析: ,故选A.
,故选A.
2.解析:


 ,∴选C.
,∴选C.
3.解析: 是增函数
是增函数 

故 ,即
,即

又

 ,故选B.
,故选B.
 4.解析:如图作出可行域,作直线
4.解析:如图作出可行域,作直线 ,平移直线
,平移直线 至
至 位置,使其经过点
位置,使其经过点 .此时目标函数取得最大值(注意
.此时目标函数取得最大值(注意 与
与 反号)
反号)
由 得
得


 ,故选A
,故选A
5.解析:设有人投中为事件 ,则
,则 ,
,

故选C.
6.解析: 展开式中能项;
展开式中能项;


由 ,得
,得 ,故选C.
,故选C.
7.解析:
由 得
得
 ,故选D.
,故选D.
8.略
9.解析:由 得准线方程
得准线方程 ,双曲线准线方程为
,双曲线准线方程为
 ,解得
,解得 ,
,
 ,故选D.
,故选D.
10.解析:设正四面体的棱长为2,取 中点为
中点为 ,连接
,连接 ,则
,则 为
为 与
与 所成的角,在
所成的角,在 中
中


 ,故选B.
,故选B.

11.解析:由题意 ,则
,则 ,故选B.
,故选B.
12.解析:由已知 ,
,
 为球的直径
为球的直径
 ,又
,又 ,
,
设 ,则
,则
 ,
,

又由 ,解得
,解得
 ,故选A.
,故选A.
另法:将四面体 置于正方休中.
置于正方休中.
正方体的对角线长为球的直径,由此得 ,然后可得
,然后可得 .
.
二、
13.解析: 在
在 上的投影是
上的投影是 .
.
14.解析: ,且
,且 .
.
15.解析: ,
,

由余弦定理 为钝角
为钝角
 ,即
,即 ,
,
解得 .
.
16.

解析:容易知命题①是错的,命题②、③都是对的,对于命题④我们考查如图所示的正方体,设棱长为 ,显然
,显然 与
与 为平面
为平面 内两条距离为
内两条距离为 的平行直线,它们在底面
的平行直线,它们在底面 内的射影
内的射影 、
、 仍为两条距离为
仍为两条距离为 的平行直线,但两平面
的平行直线,但两平面 与
与 却是相交的.
却是相交的.
三、
17.解:(1) ,
,
 ,
,
即 ,故
,故 .
.
(2)
由 得
得 .
.
设 边上的高为
边上的高为 ,则
,则
 .
.
18.(1)设甲、乙两人同时参加 灾区服务为事件
灾区服务为事件 ,则
,则 .
.
(2)记甲、乙两人同时参加同一灾区服务为事件 ,那么
,那么 .
.
(3)随机变量 可能取得值为1,2,事件“
可能取得值为1,2,事件“ ”是指有两人同时参加
”是指有两人同时参加 灾区服务,则
灾区服务,则 ,所以
,所以 .
.
 分布列是
分布列是

1
2



19.解:(1) 平面
平面
∵二面角 为直二面角,且
为直二面角,且 ,
,

 平面
平面
 平面
平面 .
.
(2)(法一)连接 与高
与高 交于
交于 ,连接
,连接 是边长为2的正方形,
是边长为2的正方形,  ,
,
 二平面
二平面 ,由三垂线定理逆定理得
,由三垂线定理逆定理得
 是二面角
是二面角 的平面角
的平面角
由(1) 平面
平面 ,
,
 .
.
在 中,
中,
∴在 中,
中,
故二面角 等于
等于 .
.
(2)(法二)利用向量法,如图以 之中点
之中点 为坐标原点建立空间坐标系
为坐标原点建立空间坐标系 ,则
,则


 ,
,
设平面 的法向量分别为
的法向量分别为 ,则由
,则由
 得
得 ,而平面
,而平面 的一个法向理
的一个法向理

故所求二面角等于 .
.
20.解:(1)由题设 ,即
,即
易知 是首项为
是首项为 、公差为2的等差数列,
、公差为2的等差数列,
∴通项公式为 ,
,
(2)由题设, ,得
,得 是以
是以 公比为
公比为 的等比数列.
的等比数列.

由 得
得 .
.
21.解:(1)由题意 ,由抛物线定义可求得曲线
,由抛物线定义可求得曲线 的方程为
的方程为 .
.
(2)证明:设 、
、 的坐标分别为
的坐标分别为
若 直线有斜率时,其坐标满足下列方程组:
直线有斜率时,其坐标满足下列方程组:
 ,
, 
若 没有斜率时,
没有斜率时, 方程为
方程为 .
.
又 .
.

 ;又
;又 ,
,

 .
.
22.(1)解: ,于是
,于是 ,
,
解得 或
或
因 ,故
,故 .
.
(2)证明:已知函数 都是奇函数.
都是奇函数.
所以函数 也是奇函数,其图象是以原点为中心的中心对称图形,而
也是奇函数,其图象是以原点为中心的中心对称图形,而 .
.
可知.函数 的图象按向量
的图象按向量 平移,即得到函数
平移,即得到函数 的图象,故函数
的图象,故函数 的图象是以点(1,1)为中心的中心对称图形,
的图象是以点(1,1)为中心的中心对称图形,
(3)证明;在曲线上作取一点 ,
,
由 知,过此点的切线方程为
知,过此点的切线方程为
 .
.
令 ,得
,得 ,切线与直线
,切线与直线 交点为
交点为 .
.
令 ,得
,得 切线与直线
切线与直线 交点为
交点为 ,直线
,直线 与直线
与直线 与直线
与直线 的交点为(1,1).
的交点为(1,1).
从而所围三角形的面积为

所以,围成三角形的面积为定值2.
www.ks5u.com