北 京 2009年 高 考 模 拟 试 卷
数学(文科)试题
题 号
一
二
三
得 分
注意事项:
1.本试题分为第Ⅰ卷和第Ⅱ卷两部分,满分150分,考试时间为120分钟。
2.答第Ⅰ卷前务必将自己的姓名、考号、考试科目涂写在答题卡上。考试结束,试题和答题卡一并收回。
3.第Ⅰ卷每题选出答案后,都必须用2B铅笔把答题卡上对应题目的答案标号(ABCD)涂黑,如需改动,必须先用橡皮擦干净,再改涂其它答案。
第Ⅰ卷
一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的,请把正确答案的代号填在题后的括号内(本大题共12个小题,每小题5分,共60分)。
1.设全集为R,集合 ,
, ,则有 ( )
,则有 ( )
A.
B.
C.
D.
2.若 是正数的充要条件是 ( )
是正数的充要条件是 ( )
A. B.
B. C.
C. D.
D.
3.在等差数列{a }中,已知a
}中,已知a =2,a
=2,a +a
+a =13,则a
=13,则a +a
+a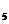 +a
+a 等于 ( )
等于 ( )
A.40
B.
4.若 ,则直线
,则直线 =1必不经过
( )
=1必不经过
( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
5.把点(3,4)按向量 平移后的坐标为
平移后的坐标为 ,则
,则 的图象按向量
的图象按向量 平移后的图象的函数表达式为 ( )
平移后的图象的函数表达式为 ( )
A.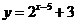 B.
B. C.
C. D.
D.
 6.如右图,正方体
6.如右图,正方体 中,E、F分别为棱
中,E、F分别为棱 和
和 中点,G为棱
中点,G为棱 上任意一点,则直线 AE与直线FG所成的角为 ( )
上任意一点,则直线 AE与直线FG所成的角为 ( )
A. B.
B.
C. D.
D.
 7.已知函数
7.已知函数 的定义域为
的定义域为 ,函数
,函数 的图象
的图象
如图所示,则函数 的图象是 ( )
的图象是 ( )

8.二项式 的展开式中含
的展开式中含 的项, 则n的一个可能值是 ( )
的项, 则n的一个可能值是 ( )
A.8 B.
9.若A, B是平面内的两个定点, 点P为该平面内动点, 且满足向量 与
与 夹角为锐角
夹角为锐角 ,
,  , 则点P的轨迹是 ( )
, 则点P的轨迹是 ( )
A.直线 (除去与直线AB的交点) B.圆 (除去与直线AB的交点)
C.椭圆 (除去与直线AB的交点) D.抛物线(除去与直线AB的交点)
10.设A、B是椭圆 =1上的两个动点,焦点坐标是F,则△ABF的周长的最大值为
=1上的两个动点,焦点坐标是F,则△ABF的周长的最大值为
( )
A.4 B.
11.数列{an}中,a1=2,  ,
,  , 又
, 又 , 则a2009= ( )
, 则a2009= ( )
A.2 B. C.
C. D.1
D.1
12.f(x)与g(x)是定义在R上的可导函数.若f ′(x)=g ′(x),则f(x)与g(x)满足 ( )
A.f(x)=g(x) B.f(x)-g(x)是常数函数
C.f(x)=g(x)=0 D.f(x)+g(x)是常数函数
第Ⅱ卷
|

 )n的展开式中第二项与第三项的系数之和等于27,则n等于 ,系数最大的项是第
项。
)n的展开式中第二项与第三项的系数之和等于27,则n等于 ,系数最大的项是第
项。 都是定义在
都是定义在 上的函数,若存在正实数
上的函数,若存在正实数 使得
使得 总成立,则称
总成立,则称 为
为 ,
, .
. 是否为
是否为 为
为 ,且
,且 18.(本大题12分)如图,直三棱柱A1B
18.(本大题12分)如图,直三棱柱A1B 与平面A
与平面A
 . 记动点C的轨迹为曲线W.
. 记动点C的轨迹为曲线W. )且斜率为k的直线l与曲线W 有两个不同的交点P和Q,
)且斜率为k的直线l与曲线W 有两个不同的交点P和Q, ),N(0, 1),在(Ⅱ)的条件下,是否存在常数k,使得向量
),N(0, 1),在(Ⅱ)的条件下,是否存在常数k,使得向量 与
与 共线?如果存在,求出k的值;如果不存在,请说明理由.
共线?如果存在,求出k的值;如果不存在,请说明理由. 的前n项和为Tn,求证:Tn<2.
的前n项和为Tn,求证:Tn<2.  故选D
故选D 得d=3,a5=14,
得d=3,a5=14, =
= 故选B
故选B ,则
,则 ,则
,则 的图象按向量
的图象按向量 平移后的图象的函数表达式为:
平移后的图象的函数表达式为: ,即
,即 ,故选D。
,故选D。 的图像相同,故可排除(A)、(C)、(D).故选B
的图像相同,故可排除(A)、(C)、(D).故选B 令
令 =5,得3n=5r+10 , 当r=1时,n=5.故选C
=5,得3n=5r+10 , 当r=1时,n=5.故选C 9. 提示由
9. 提示由 ,得
,得 ,所以
,所以 , 点P的轨迹是圆(除去与直线AB的交点).故选B
, 点P的轨迹是圆(除去与直线AB的交点).故选B , a3=
, a3=  , a4 =2,
, a4 =2,  (x
(x )n-r(-
)n-r(- )r,由题意知:-
)r,由题意知:- +
+ =27
=27 n=9
n=9 ;矩形;若
;矩形;若  则以
则以  为邻边的平行四边形对角线相等,所以此四边形必为矩形,可见
为邻边的平行四边形对角线相等,所以此四边形必为矩形,可见 ;提示: P=1-
;提示: P=1- =
= 提示:当直角三角形的斜边垂直与平面时,所求面积最大。
提示:当直角三角形的斜边垂直与平面时,所求面积最大。 是
是 在
在 上的生成函数,则存在正实数
上的生成函数,则存在正实数 使得
使得 恒成立,令
恒成立,令 ,得
,得 ,与
,与 矛盾,
矛盾, ,因为
,因为 
 ,当且仅当
,当且仅当 且
且 时等号成立,
时等号成立, 时
时
 ,
, ,
,
 ………………………10分
………………………10分 为
为 与平面A
与平面A .
. 与平面A
与平面A .…………4分
.…………4分 ,
, .
.  .……………………8分
.……………………8分 种所选2人的血型为O型或A型的的情况共有
种所选2人的血型为O型或A型的的情况共有 种故所求概率为
种故所求概率为 ?…………6分
?…………6分 …………12分
…………12分 ,
,  ,
,  ,
, 的椭圆除去与x轴的两个交点.
的椭圆除去与x轴的两个交点. .
.  .
.
 .………………… 2分
.………………… 2分 ,
, .
. .
①………………………… 5分
.
①………………………… 5分 ,
, 或
或 .
. ………… 7分
………… 7分 =(x1+x2,y1+y2),
=(x1+x2,y1+y2), .
②
.
② ③
③ ,
, ,
,  .……………………… 11分
.……………………… 11分 共线等价于
共线等价于 .
. .
.


 …………7分
…………7分

 …………10分
…………10分
 ………………12分
………………12分