吉林省吉林市2009届高三下学期期中复习检测
数 学(文科)
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共22小题,共150分,共4页,考试时间120分钟,考试结束后,将答题卡和试题卷一并交回。
注意事项:1.答题前,考生务必将自己的姓名、准考证号码填写清楚,将条形码准确粘贴在条形码区域内.
2.选择题必须使用2B铅笔填涂,非选择题必须使用0.5毫米黑色字迹的签字笔书写,字体工整、笔迹清楚.
3.请按照题号顺序在各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸上、试题卷上的答题无效.
4.做图可先用铅笔画出,确定后必须用黑色字迹的签字笔描黑.
5.保持卡面清洁,不要折叠、不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀.
参考公式:
如果事件A、B互斥,那么 球的表面积公式
 =
=

如果事件A、B相互独立,那么 其中R表示球的半径
 ?
? =
= ?
? 球的体积公式
球的体积公式
如果事件A在一次试验中发生的概率是P,那

么n次独立重复试验中恰好发生k次的概率 其中R表示球的半径
Pn(k) = P k(1- P)n-k(k=0,1,2,…,n)
P k(1- P)n-k(k=0,1,2,…,n)
第Ⅰ卷(选择题 共60分)
一、选择题:本大题共12题,每小题5分,共60分,在每小题给出的四个选项中,只有一个是符合题目要求。
1.已知集合 ,
, ,则M∩N =
,则M∩N =
A. B.
B.
C. D.
D.
2.已知向量
 ,
,
 且a⊥b ,则
且a⊥b ,则
A.3 B. D.
D.
3.在等差数列 中,若
中,若 ,则
,则
A. B.
B. C.
C. D.1
D.1
4.已知双曲线 的两个焦点坐标分别为
的两个焦点坐标分别为 , 则双曲线的离心率为
, 则双曲线的离心率为
A. B.
B. C.
C. D.
D.
|
 在点(1,1)处的切线与直线ax+y+1=0平行,则
在点(1,1)处的切线与直线ax+y+1=0平行,则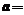
 ,则角B的值是
,则角B的值是
 B.
B. C.
C. D.
D.
 上,横坐标为4的点到焦点的距离为5,则p的值为
上,横坐标为4的点到焦点的距离为5,则p的值为  B.1 C.2
D.4
B.1 C.2
D.4  ,则
,则 B.
B.
 D.
D.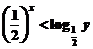
 的图象按向量e平移恰好得到一个偶函数的图象,则e可能是
的图象按向量e平移恰好得到一个偶函数的图象,则e可能是 B.
B.
 C.
C.
 D.
D.
 ,则该正三棱锥的体积为A.
,则该正三棱锥的体积为A. B.
B.
 C.
C. 
 D.
D. 
 的展开式中的常数项是________________. (用数字作答)
的展开式中的常数项是________________. (用数字作答) 的各顶点都在同一个球面上,其中
的各顶点都在同一个球面上,其中 ,
, ,
, ,则A,B两点的球面距离为___________.
,则A,B两点的球面距离为___________. 中,
中, ,
, .
.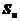 ,证明:
,证明: 16(n =1,2,3 …).
16(n =1,2,3 …).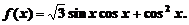
 的最小正周期及单调递增区间;
的最小正周期及单调递增区间; 时,求函数
时,求函数 取何值时函数
取何值时函数 ,本场比赛采用三局两胜制,即先胜两局者获胜,比赛结束.设各局比赛相互没有影响.
,本场比赛采用三局两胜制,即先胜两局者获胜,比赛结束.设各局比赛相互没有影响. 的事件
的事件 的概率;
的概率; 的概率.
的概率. 20.(本小题满分12分)
20.(本小题满分12分) 中,AC=BC=2,
中,AC=BC=2, =
= ,点D是AB的中点,点E是
,点D是AB的中点,点E是
 ⊥平面CDE;
⊥平面CDE;
 (Ⅱ)求二面角
(Ⅱ)求二面角 的大小.
的大小.  (a,b∈R)在
(a,b∈R)在 处取得极值,且
处取得极值,且 .
. ,使得
,使得 ,求b的取值范围.
,求b的取值范围. 22.(本小题满分12分)
22.(本小题满分12分)  ,1).
,1). ,0)的动直线l交椭圆C于A、B两点,试
,0)的动直线l交椭圆C于A、B两点,试
 ;16 .446.
;16 .446. 的公比为q(q>0),依题意可得
的公比为q(q>0),依题意可得 解得
解得 (5分)
(5分) (6分)
(6分) (10分)
(10分) (2分)∴
(2分)∴ ; (4分)
; (4分) ,即
,即 ,
, 时
时 单调递增
单调递增 (6分)
(6分) ,∴
,∴ ,∴
,∴ (10分)
(10分) 时,
时, 有最大值
有最大值 ,此时
,此时 .
(12分)
.
(12分) 表示甲以
表示甲以 获胜;
获胜; 表示乙以
表示乙以 ,
,
 (6分)
(6分) (Ⅱ)
(Ⅱ) 记表示甲以
记表示甲以 获胜;
获胜; 表示甲以
表示甲以 , ∴
, ∴ (12分)
(12分) 中,
中, 面ABC,又D为AB中点,∴CD⊥面
面ABC,又D为AB中点,∴CD⊥面 ,∴CD⊥
,∴CD⊥ ,∴
,∴ ,
, 的
的 ∵
∵ ,
, ,又由△ENM △EDC得
,又由△ENM △EDC得 .
又∵
.
又∵
 , (12分)
, (12分) 的大小为
的大小为 . (12分)
. (12分) 解法二:AC=BC=2,AB=
解法二:AC=BC=2,AB= ,可得AC⊥BC,故可以C为坐标原点建立如图所示直角
,可得AC⊥BC,故可以C为坐标原点建立如图所示直角 ),
), (2,0,
(2,0, )(3分)
)(3分) (-2,2,-
(-2,2,- (1,1,0),
(1,1,0), (0,2,
(0,2, ,
,
 ,
, 又CE∩CD =C
又CE∩CD =C (2,0,
(2,0, ,n
,n 得
得 ,
,
 得
得 ,
, ,n=(2,1,
,n=(2,1, )
(9分)
)
(9分) 等于二面角
等于二面角 .
(12分)
.
(12分)  .
(12分)
.
(12分) .由题意知
.由题意知 为方程
为方程 的两根
的两根 ,得
,得 (3分)
(3分) ,
, .
. 时,
时, ;当
;当 和
和 时,
时,
 在
在 上单调递减,在
上单调递减,在 ,
, 上单调递增. (7分)
上单调递增. (7分) 处取得极值,此时
处取得极值,此时 ,若存在
,若存在 ,使得
,使得 ,
, 就是
就是 解得
解得 .
(12分)
.
(12分) . (12分)
. (12分)
 (a>b>0),由已知c=1,
(a>b>0),由已知c=1, . 所以a=
. 所以a= ,b2=a2-c2=1,
,b2=a2-c2=1, + x2
=1. (4分)
+ x2
=1. (4分) )2+y2=
)2+y2= .
. 解得
解得 即两圆相切于点(1,0).
即两圆相切于点(1,0). 即(k2+2)x2+
即(k2+2)x2+ k2x+
k2x+ k2-2=0.
k2-2=0.
 =(x1-1, y1),
=(x1-1, y1),  =(x2-1, y2),
=(x2-1, y2), +(
+( +
+
 +1=0, (11分)
+1=0, (11分)