南充市二00六年高中阶段学校招生统一考试
数 学 试 卷
(满分100分,考试时间90分)
一、选择题(本大题共8个小题,每小题2.5分,共20分)
以下每小题都有代号为A、B、C、D的四个答案选项,其中只有一个是正确的,请把正确选项的代号填在相应的括号内.填写正确计2. 5分,不填、填错或填出的代号超过一个记0分.
1.下列式子中与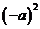 计算结果相同的是( )
计算结果相同的是( )
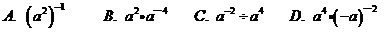
2,下列图形中,能肯定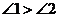 的是( )
的是( )
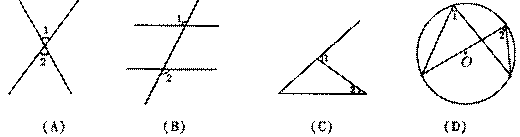
3.已知a <0,那么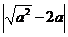 可化简为( )
可化简为( )
A. -a B. a C. -3a D.3a
4.等腰三角形的底和腰是方程x2-6x+8=0的两根,则这个三角形的周长为( )
A.8 B.10 C.8或10 D.不能确定
5.某车间6月上旬生产零件的次品数如下(单位:个):
0,2,0,2,3,0,2,3,1,2,
则在这10天中该车间生产零件的次品数的( )
A.众数是4 B.中位数是1.5
C.平均数是2 D.方差是1.25
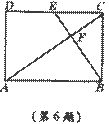
6.如图,矩形ABCD中,BE ⊥AC于F,E恰是CD的中点,下列式子成立的是( )

7.二次函数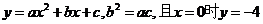 则( )
则( )
A.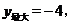 B.
B.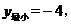
 C.
C.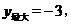 D.
D.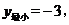
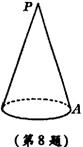
8.如图,底面半径为1,母线长为4的圆锥,一只小蚂蚁若从A点出发,绕侧面一周又回到A点,它爬行的最短路线长是( )
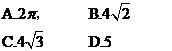
将答案直接填在题中横线上.
二、填空题(本大题共4个小题,每小题2.5分,共10分)
9.若不等式-3x+n>0的解集是x<2,则不等式-3x +n <0的解集是_____________
10.如果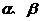 是一元二次方程
是一元二次方程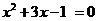 的两个根,那么
的两个根,那么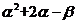 的值是___________
的值是___________
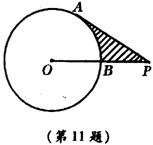 11.如图,PA切圆O于A,OP交圆O于B,且PB=1,PA=
11.如图,PA切圆O于A,OP交圆O于B,且PB=1,PA=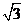 ,则阴影部分的面积S=____________.
,则阴影部分的面积S=____________.
12.老师给出一个函数,甲、乙各指出了这个函数的一个性质:
甲:第一、三象限有它的图象;
乙:在每个象限内,y随x的增大而减小.
请你写一个满足上述性质的函数______________________
三、(本大题共2个小题,每小题6分,共12分)
13.计算:
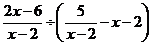
14.有规律排列的一列数:2,4,6,8,10,12,…
它的每一项可用式子2n(n是正整数)来表示.
有规律排列的一列数:1,-2,3,- 4,5,-6,7,-8,…
(1)它的每一项你认为可用怎样的式子来表示?
(2)它的第100个数是多少?
(3) 2006是不是这列数中的数?如果是,是第几个数?
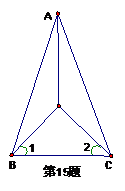
四、(本大题共2个小题,每小题8分,共16分)
15.已知:如图,OA平分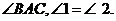
求证:△ABC是等腰三角形.
16 A、B两城铁路长240千米,为使行驶时间减少20分,需要提速10千米/时,但在现有条件下安全行驶限速100千米/时,问能否实现提速目标.
五、(本大题共2个小题,每小题8分,共16分)
17.如图,湖中有建筑物AB,某人站在建筑物顶部A在岸上的投影处C,发现自己的影长与 身高相等.他沿BC方向走30 m到D处,测得顶部A的仰角为300.求建筑物AB的高.
18.学校计划购买40支钢笔,若干本笔记本(笔记本数超过钢笔数).甲、乙两家文具店的标价都是钢笔10元/支,笔记本2元/本,甲店的优惠方式是钢笔打9折,笔记本打8折;乙店的优惠方式是每买5支钢笔送1本笔记本,钢笔不打折,购买的笔记本打7.5折,试问购买笔记本数在什么范围内到甲店更合算。
六、(本大题共2个小题,每小题8分,共16分)
19.已知点A(0,-6),B(-3,0),C(m,2)三点在同一直线上,试求出图象经过其中一点的反比例函数的解析式并画出其图象.(要求标出必要的点,可不写画法.)
20.如图,PAB、PCD是圆O的两条割线,AB是圆O的直径,AC//OD.
 (1)求证:CD=_________(先填后证).
(1)求证:CD=_________(先填后证).
(2)若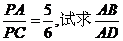 的值.
的值.
七、(本题满分10分)
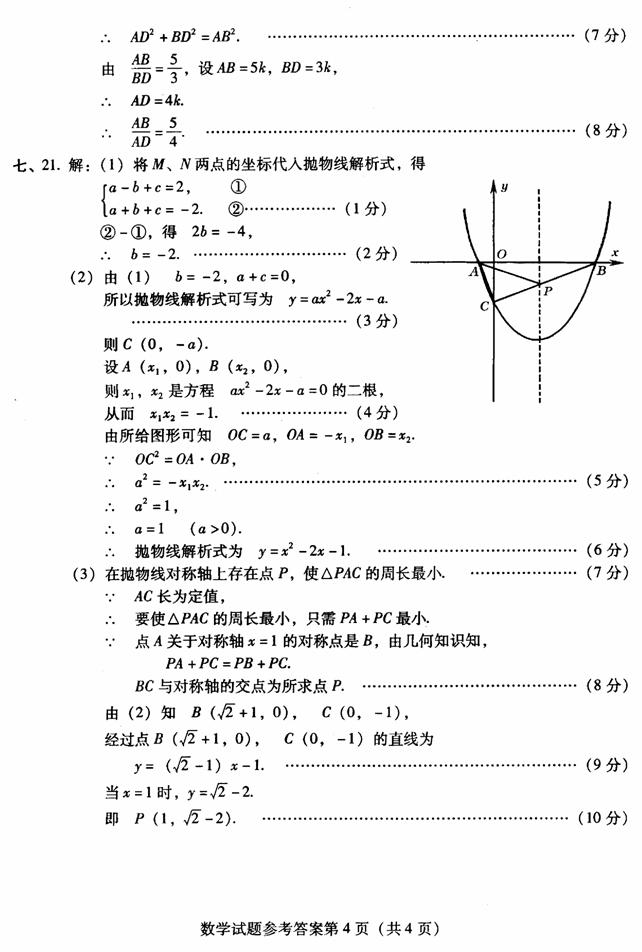
21.如图,经过点M(-1,2),N(1,-2)的抛物线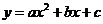 与x轴交于A、B两点,与y轴交于C点.
与x轴交于A、B两点,与y轴交于C点.
(1)求b的值.
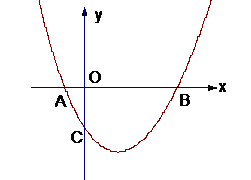 (2)若OC2=OA?OB,试求抛物线的解析式.
(2)若OC2=OA?OB,试求抛物线的解析式.
(3)在该抛物线的对称轴上是否存在点P,使ㄓPAC的周长最小?若存在,求出点P的坐标;若不存在,请说明理由.