山东省潍坊中学
高三上学期模块检测(二)
数学试题(文科)
注意事项:
1.本试题满分150分,考试时间为120分钟.
2.使用答题卡时,必须使用0.5毫米的黑色墨水签字笔书写,作图时,可用2B铅笔.要字迹工整,笔迹清晰.严格在题号所指示的答题区域内作答.超出答题区书写的答案无效;在草稿纸,试题卷上答题无效.
3.答卷前将密封线内的项目填写清楚.
一、选择题:本大题共12小题,每小题5分,共
1.已知全集U={一l,0,1,2},集合A={一l,2},B={O,2},则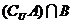 = ( )
= ( )
A.{0} B.{2} C.{0,l,2} D. Ø
Ø
2.在ΔABC,BC=2,角B=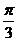 ,当ΔABC的面积等于
,当ΔABC的面积等于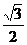 时,sinC= ( )
时,sinC= ( )
A.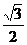 B.
B.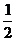 C.
C.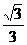 D.
D.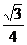
3.用一些棱长是lcm的小正方体码放成一个几何体,图l为其俯视图,图2为其正视图,则这个几何体的体积最多是 ( )

A.
4.函数f(x)=lnx+2x-l零点的个数为 ( )
A.0 B.
5.若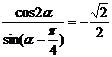 ,则cos
,则cos 的值为 ( )
的值为 ( )
A.-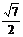 B.-
B.-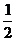 C.
C.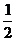 D.
D.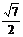
6.设F1,F2分别是双曲线x2一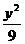 =l的左、右焦点,若点p在双曲线上,且
=l的左、右焦点,若点p在双曲线上,且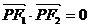 ,则
,则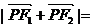 ( )
( )
A.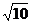 B.
B.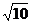 C.
C.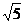 D.2
D.2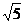
7.在等比数列{an}中,若a3a5 a7a9=243,则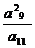 的值为 ( )
的值为 ( )
A.9 B.1 C.2 D.3
8.已知非零向量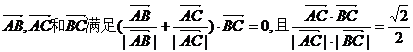 ( )
( )
A.等边三角形 B.等腰非直角三角形
C.非等腰三角形 D.等腰直角三角形
9.已知动圆过点(1,0),且与直线x=一l相切,则动圆圆心的轨迹方程为 ( )
A.x2+y2=l B.x2-y2=1 C.y2=4x D.x=0
10.若实数x,y满足不等式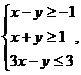 ,则z=4x+y的最大值为 ( )
,则z=4x+y的最大值为 ( )
A.4 B.11 C.12 D.14
11.已知函数f(x)满足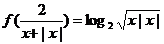 ,则f(x)的解析式是 ( )
,则f(x)的解析式是 ( )
A.f(x)=log2x B.f(x)=- log2x
C.f(x)=2-x D.f(x)=x-2
12.关于函数f(x)=x-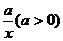 ,有下列四个命题:①f(x)的值域是(一∞,0)
,有下列四个命题:①f(x)的值域是(一∞,0)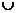 (0,+∞);
(0,+∞);
②f(x)是奇函数;③f(x)在(一∞,0) 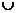 (0,+∞)上单调递增;④方程|f(x)
|=a总有四个不同的解,其中正确的是 ( )
(0,+∞)上单调递增;④方程|f(x)
|=a总有四个不同的解,其中正确的是 ( )
A.仅②④ B.仅②③ C.仅①② D.仅③④
二、填空题:本大题有4个小题,每小题4分,共16分;将答案填在答题纸的对应位置
13.一个长方体的各顶点均在同一球的球面上,且一个顶点上的三条棱的长分别为2,2,3,则此球的表面积为 .
14.已知抛物线型拱桥的顶点距离水面2米时,测量水面宽为8米,当水面上升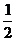 米后,水面的宽度是
.
米后,水面的宽度是
.
15.已知点P在曲线f(x)=x4一x上,曲线在点p处的切线平行于直线3x―y=o,则点P的坐标为
16.若函数f(x)=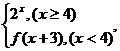 则f(log23)=
则f(log23)=
三、解答题:本大题共6个小题,满分74分.解答时要求写出必要的文字说明、证明过程或推演步骤。
17.(本题满分12分)
设函数f(x)=a?b,其中向量a=(2cosx,1),b=(cosx,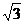 sin2x+m).
sin2x+m).
(1)求函数f(x)的最小正周期和在[0,π]上的单调递增区间;
(2)当x∈[0,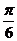 ]时,f(x)的最大值为4,求m的值.
]时,f(x)的最大值为4,求m的值.
18.(本题满分12分)
设某市现有从事第二产业人员100万人,平均每人每年创造产值a万元(a为正常数),
现在决定从中分流x万人去加强第三产业.分流后,继续从事第二产业的人员平均每人每年创造产值可增加2x%(O<x<100).而分流出的从事第三产业的人员,平均每人每年可创造产值1.2a万元.
(1)若要保证第二产业的产值不减少,求x的取值范围;
(2)在(1)的条件下,问应分流出多少人,才能使该市第二、三产业的总产值增加最多?
19.(本题满分12分)
如图,已知三棱锥A―BPC中,AP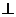 PC.AC
PC.AC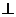 BC.M为AB中点.D为PB中点.且△PMB为正三角形.
BC.M为AB中点.D为PB中点.且△PMB为正三角形.
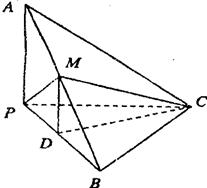 (1)求证:DM//平面APC;
(1)求证:DM//平面APC;
(2)求证:平面ABC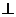 平面APC;
平面APC;
(3)若BC=4,AB=20,求三棱锥D―BCM体积
20.(本题满分12分)
设函数g(x)=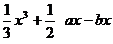 (a,b∈R),在其图象上一点P(x,y)处的切线的斜率记为f(x).
(a,b∈R),在其图象上一点P(x,y)处的切线的斜率记为f(x).
(1)若方程f(x)=0有两个实根分别为一2和4,求f(x)的表达式;
(2)若g(x)在区间[一1,3]上是单调递减函数,求a2+b2的最小值.
21.(本题满分12分)
|
 的焦点,离心率为
的焦点,离心率为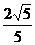
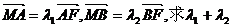 的值。
的值。 15. (1.0) 16.24
15. (1.0) 16.24 )+m+1,…………………2分
)+m+1,…………………2分 ]………6分
]………6分 …………3分
…………3分
 0≤x≤50 …………6分
0≤x≤50 …………6分 。…………10分
。…………10分 19.(本小题12分)
19.(本小题12分) 平面ABC
平面ABC 
 ΔPBC=
ΔPBC=
 AP=
AP= =5
=5 SΔBDC
SΔBDC ----------------------12分
----------------------12分 ,∴
,∴ ,f(x)= x2-2x-8-----------------------5分
,f(x)= x2-2x-8-----------------------5分 即可,也即
即可,也即
 时,a2+b2有最小值13---------------------------------------12分
时,a2+b2有最小值13---------------------------------------12分 …………………………………………6分
…………………………………………6分 且不讨论n=1,扣1分)……………………………………8分
且不讨论n=1,扣1分)……………………………………8分 (a>b>0),-------------------------------- 1分
(a>b>0),-------------------------------- 1分 ,
,
 +y2=1并整理,
+y2=1并整理, , x1 x2=
, x1 x2= --------------------------------------------------------10分
--------------------------------------------------------10分
 (2- x1,- y1),( x2-0, y2-y0)=
(2- x1,- y1),( x2-0, y2-y0)=
 (2- x2,- y2)
(2- x2,- y2) ,-------------------------------------------------------------12分
,-------------------------------------------------------------12分 ………………14分
………………14分