山东省潍坊中学
高三上学期模块检测(二)
数学试题(理科)
注意事项:
1.本试题满分150分,考试时间为120分钟.
2.使用答题纸时,必须使用0.5毫米的黑色墨水签字笔书写,作图时,可用2B铅笔.
要字迹工整,笔迹清晰.严格在题号所指示的答题区域内作答.超出答题区书写的答案无效;在草稿纸,试题卷上答题无效.
3.答卷前将密封线内的项目填写清楚.
一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只
1.已知全集U={一1,0,1,2},集合A={一l,2},B={O,2},则(CuA)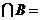 ( )
( )
A.{0} B.{2} C.{0,1,2} D.Ø
2.若ΔABC是锐角三角形,向量p=(sinA,cosA),q=(sinB,-cosB),则p与q的夹
角为 ( )
A.锐角 B.直角 C.钝角 D.以上均不对
 3.设f′(x)是函数f(x)的导函数,将y= f(x)和y= f′(x)的图象画在同一直角坐标系中,不可能正确的是 ( )
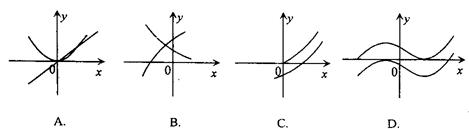
3.设f′(x)是函数f(x)的导函数,将y= f(x)和y= f′(x)的图象画在同一直角坐标系中,不可能正确的是 ( )
4.已知直线l和平面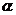 、
、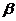 满足l
满足l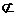
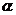 ,l
,l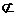
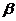 .在l∥
.在l∥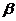 ,l
,l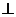
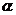 ,
,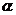
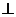
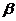 这三个关系中,以其中两个作为条件,余下―个作为结论所构成的命题中,真命题的个数是 ( )
这三个关系中,以其中两个作为条件,余下―个作为结论所构成的命题中,真命题的个数是 ( )
A.0 B.
5.从抛物线y2=4x上一点P引抛物线准线的垂线,垂足为M,且|PM|=5,设抛物线的焦
点为F,则△MPF的面积为 ( )
A.5 B.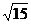
6.已知,f(x)=cos2x―l,g(x)=f(x+m)+n,则使g(x)为奇函数的实数m,n的可能取值为( )
A.m=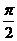 ,n=一1 B.m=
,n=一1 B.m=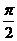 ,n=1
,n=1
C.m=-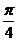 ,n=一1 D.m=-
,n=一1 D.m=-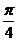 , n=1
, n=1
7.在等比数列{an}中,若a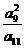 的值为 ( )
的值为 ( )
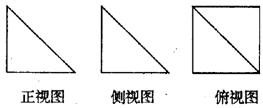 A.9 B.
A.9 B.
8.一个几何体的三视图如图所示,其中正视
图和侧视图是腰长为4的两个全等的等
腰直角三角形.若该几何体的体积为V,
并且可以用n个这样的几何体拼成―个
棱长为4的正方体,则V,n的值是( )
A.V=32,n=2 B.V=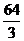 , n=3
, n=3
C.V=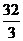 , n=6 D.V=16,n=4
, n=6 D.V=16,n=4
9.若圆x2+y2-ax+2y+1=0与圆x2+y2=1关于直线y=x-1对称,过点C(-a,a)的圆与y轴相切,则圆心P的轨迹方程为 ( )
A.y2-4x+4y+8=0 B.y2+2x-2y+2=0
C.y2+4x-4y+8=0 D.y2-2x-y-1=0
10.若实数x,y满足不等式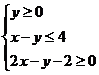 ,则
,则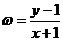 的取值范围是 ( )
的取值范围是 ( )
A.[-l,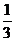 ] B.[
] B.[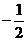 ,
,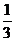 ] C.[
] C.[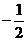 ,2] D.[
,2] D.[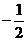 ,+
,+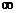 )
)
11.函数f(x)=sin2x+2cosx在区间[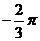 ,
,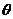 ]上的最大值为l,则
]上的最大值为l,则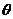 的值是 ( )
的值是 ( )
A.0 B.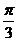 C.
C.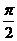 D.
D.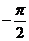
12.定义:若存在常数k,使得对定义域D内的任意两个不同的实数x1,x2均有|f(x1)-f(x2)|≤k|x1-x2|成立,则称函数f(x)在定义域D上满足利普希茨条件.对于函数f(x)=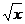 (x≥1)满足利普希茨条件,则常数k的最小值应是 ( )
(x≥1)满足利普希茨条件,则常数k的最小值应是 ( )
A.2
B.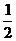 D.
D.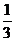
二、填空题:本大题有4个小题,每小题4分,共16分:将答案填在答题卡上
13.若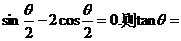 .
.
14.若数列{an}满足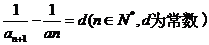 ,则称数列{ an }为调和数列.已
,则称数列{ an }为调和数列.已
知数列{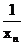 }为调和数列,且
}为调和数列,且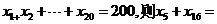 .
.
 15.已知长方体ABCD―A1B
15.已知长方体ABCD―A1B
则ΔAA1B,ΔABD,ΔAA1D面积之和的最大值为 .
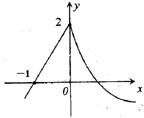
16.函数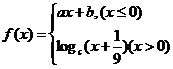 的图象如图所示,
的图象如图所示,
则a+b+c= .
程或推演步骤.
三、解答题:本大题共6个小题,满分74分.解答时要求写出必要的文字说明、证明过
17.(本题满分12分)
设函数f(x)=a•b,其中向量a=(2cosx ,1),b=(cosx, 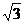 sin2x+m).
sin2x+m).
(1)求函数f(x)的最小正周期和在[0,π]上的单调递增区间;
(2)当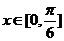 时,?4< f(x)<4恒成立,求实数m的取值范围.
时,?4< f(x)<4恒成立,求实数m的取值范围.
18.(本题满分12分)四棱锥P-ABCD中,PA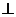 面ABCD,PA=AB=BC=2,E为PA中点,过E作平行于底面的面EFGH分别与另外三条侧棱交于只F, G, H,已知底面ABCD为直角梯形,AD∥BC, AB
面ABCD,PA=AB=BC=2,E为PA中点,过E作平行于底面的面EFGH分别与另外三条侧棱交于只F, G, H,已知底面ABCD为直角梯形,AD∥BC, AB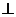 AD,∠BCD=135°.
AD,∠BCD=135°.
(1)求异面直线AF,BG所成的角的大小;
(2)设面APB与面CPD所成的锐二面角的大小为θ,求cosθ.

19.(本题满分12分)
某国由于可耕地面积少,计划从今年起的五年填湖围造一部分生产和生活用地,若填湖费、购置排水设备费等所需经费与当年所填湖造地面积x(亩)的平方成正比,其比例系数为a,设每亩水面的年平均经济效益为b元,填湖造地后的每亩土地的年平均收益为c元(其中a,b,c均为常数,且c>b).
(1)若按计划填湖造地,且使得今年的收益不小于支出,试求所填面积x的最大值;
(2)如果填湖造地面积按每年l%的速度减少,为保证水面的蓄洪能力和环保要求,填
湖造地的总面积不能超过现有水面面积的25%,求今年填湖造地的面积最多只能占现有水面的百分之几.
注:根据下列近似值进行计算:
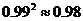 ,
, 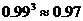 ,
, 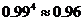 ,
,  ,
, 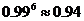 ,
, 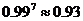
20.(本小题满分12分)
设函数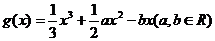 ,在其图象上一点P(x,y)处的切线的斜率记为f(x)。
,在其图象上一点P(x,y)处的切线的斜率记为f(x)。
(1)若方程f(x)=0有两个实根分别为-2和4,求f(x)的表达式;
(2)若g(x)在区间[-1,3]上是单调递减函数,求a2+b2的最小值.
21.(本题满分12分)
已知动点A、B分别在x轴、y轴上,且满足|AB|=2,点P在线段AB上,且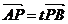 (t是不为零的常数).设点P的轨迹方程为C。
(t是不为零的常数).设点P的轨迹方程为C。
(1)求点P的轨迹方程C;
(2)若t=2,点M、N是C上关于原点对称的两个动点(M、N不在坐标轴上),点Q坐标为(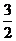 ,3),求ΔQMN的面积S的最大值。
,3),求ΔQMN的面积S的最大值。
22.(本题满分14分)
设向量a=(x,2),b=(x+n,2x-1)(n∈N+),函数y=a?b在[0,1]上的最小值与最大值的和为an,又数列{bn}满足:
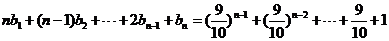 .
.
(1)求证:an=n+1.
(2)求bn的表达式;
|
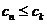 成立?证明你的结论.
成立?证明你的结论. 14.20 15.32 16.
14.20 15.32 16.
 ………………2分
………………2分 .………………………………4分
.………………………………4分 .…………………6分
.…………………6分 ,
, ,………………………………………8分
,………………………………………8分 …………………………………………10分
…………………………………………10分 …………………………………………12分
…………………………………………12分
 =(1,0,1),
=(1,0,1), =(一1,1,1),
=(一1,1,1), ……………………………4分
……………………………4分
 …………………………12分
…………………………12分 ,
, .……………………………………3分
.……………………………………3分 时,此时所填面积的最大值为
时,此时所填面积的最大值为 亩……………………………7分
亩……………………………7分 ,………………9分
,………………9分 ,所以
,所以 .
. ………………………………12分
………………………………12分 ,………………5分
,………………5分 横成立
横成立
 内的点到原点距离的平方,其中点(-2,3)距离原点最近.所以当
内的点到原点距离的平方,其中点(-2,3)距离原点最近.所以当 时,a2+b2 有最小值13. ………………………………12分
时,a2+b2 有最小值13. ………………………………12分 ,即
,即 ……………………………2分
……………………………2分 ,由题意知t>0,
,由题意知t>0, 即
即
 点P的轨迹方程C为:
点P的轨迹方程C为: .…………………………4分
.…………………………4分 .………………………………………5分
.………………………………………5分

 …………………………………………………………………………7分
…………………………………………………………………………7分 .…………………………………8分
.…………………………………8分


 …………………………………………………………11分
…………………………………………………………11分
 时,等号成立
时,等号成立 ……………………………………………………12分
……………………………………………………12分 ,因为对称轴
,因为对称轴 ,所以在[0,1]上为增函数,
,所以在[0,1]上为增函数, .……………………………………………………4分
.……………………………………………………4分

 , ………………7分
, ………………7分
 ………………9分
………………9分 …………10分
…………10分 c2> c1
c2> c1 =2时,cn+1-cn=(
=2时,cn+1-cn=( )n-2
)n-2
 ,
, ck成立。 …………14分
ck成立。 …………14分