重庆市丰都中学2009届高三第五次月考
数学(理科) 试题
第I卷(选择题: 共50分)
一.选择题(本大题共10小题,每小题5分,共50分)在每小题给出的四个选项中,只有一项是符合题目要求的,把正确选项的代号填涂在机读卡的相应位置上。
1.已知全集I=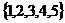 ,A=
,A=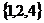 ,B=
,B=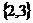 ,则CI(
,则CI(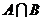 )=
)=
A.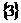 B.
B.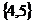 C.
C.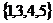 D.
D.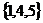
2.如果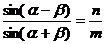 ,则
,则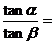
A.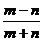 B.
B. C.
C.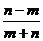 D.
D.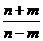
3.平面内到定点M(2,2)与到定直线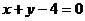 的距离相等的点的轨迹是
的距离相等的点的轨迹是
A.直线 B.抛物线 C.椭圆 D.双曲线
4.函数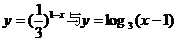 (其中a>0且
(其中a>0且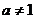 )的图象关于
)的图象关于
A.直线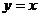 对称
B.直线
对称
B.直线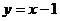 对称
对称
C.直线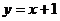 对称
D.直线
对称
D.直线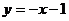 对称
对称
5.已知数列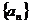 为等差数列,且
为等差数列,且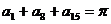 ,则
,则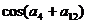 的值为
的值为
A.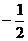 B.
B.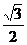 C.
C.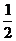 D.
D.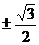
|
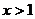
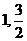 ) B.(1,3]
C.(
) B.(1,3]
C.(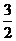 ,2] D.
,2] D.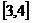
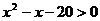 ,q:
,q: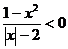 ,则p是q的
,则p是q的 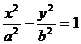 和椭圆
和椭圆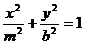 (
(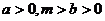 )的离心率之积大于1,那么以a.b.m为边长的三角形是
)的离心率之积大于1,那么以a.b.m为边长的三角形是 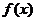 的定义域为R,且
的定义域为R,且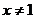 ,已知
,已知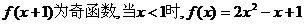 ,那么当
,那么当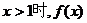 的递增区间是
的递增区间是
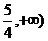 B.
B.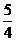 )
C.
)
C.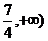 D.
D.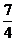
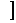
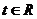 ,都有
,都有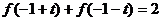 ,若
,若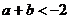 ,则有
,则有 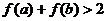 B.
B.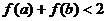
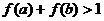 D.
D.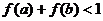
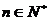 ,都有
,都有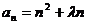 恒成立,则实数
恒成立,则实数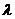 的取值范围是
.
的取值范围是
.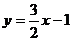 与曲线
与曲线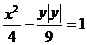 的公共点个数是
.
的公共点个数是
.
 ,将函数
,将函数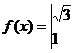
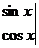 的图象沿向量
的图象沿向量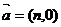 ,其中n>0,平移后所得图象对应的函数为奇函数,则n的最小值为
.
,其中n>0,平移后所得图象对应的函数为奇函数,则n的最小值为
.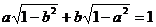 ,则a+b的取值范围是
.
,则a+b的取值范围是
.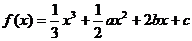 ,若当
,若当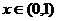 时,
时,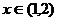 时,
时,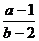 的取值范围是
.
的取值范围是
.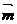 =(sinB,1-cosB)与向量
=(sinB,1-cosB)与向量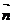 =(2,0),夹角
=(2,0),夹角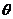 的余弦值为
的余弦值为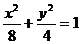 有相同的焦点,直线
有相同的焦点,直线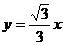 为C的一条渐近线
为C的一条渐近线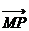 ?
?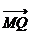 的范围.
的范围.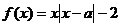
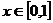 时,恒有
时,恒有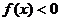 ,求实数a的取值范围.
,求实数a的取值范围.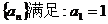 ,
, 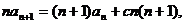 (c为常数)
(c为常数) ;
;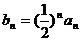 ,是否存在常数c,使数列
,是否存在常数c,使数列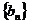 为递减数列,若存在,求出c的值,若不存在,说明理由.
为递减数列,若存在,求出c的值,若不存在,说明理由.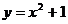 的两条切线AP.AQ,P.Q为切点
的两条切线AP.AQ,P.Q为切点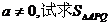 :|OA|的最小值.
:|OA|的最小值.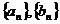 满足
满足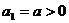 ,
,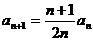 ,且
,且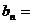
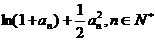
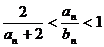 ;
;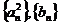 的前
的前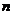 项和分别为
项和分别为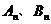 ,证明:
,证明: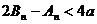 .
. 12.(
12.( )
13.2
14.
)
13.2
14. 15.
15.
 17,解:①
17,解:①
 =2(1,0)
(2分)
=2(1,0)
(2分)
 ?
? ,
(4分)
,
(4分) cos
cos =
=
 ,
,  ,
,  即B=
即B=
 (7分)
(7分)
 (9分)
(9分) ,
,  (11分)
(11分)
 的取值范围是(
的取值范围是( ,1
,1 (13分)
(13分) (
( ) (1分)
) (1分) ,求得两焦点
,求得两焦点 ,
, (3分)
(3分) ,又
,又 为一条渐近线
为一条渐近线 , 解得:
, 解得: (5分)
(5分) (6分)
(6分) ,则
,则 (7分)
(7分)


 ?
? (9分)
(9分) ,
,  (10分)
(10分)
 (11分)
(11分)
 (13分)
(13分)
 单减区间为[
单减区间为[ ] (6分)
] (6分) (8分)
(8分) ,
,
 , (
, ( ),
), ,
,
 (10分)
(10分) ,
,
 (11分)
(11分) 在(0,1]上单调递减
在(0,1]上单调递减  (12分)
(12分) (13分)
(13分)

 (2分)
(2分) }是首项为1,公差为C的等差数列
}是首项为1,公差为C的等差数列 即
即 (4分)
(4分)


 即
即 ………………※
(6分)
………………※
(6分) (8分)
(8分) (9分)
(9分)
 (
( )
)
 (11分)
(11分)




 (12分)
(12分) 的切线斜率为K,则切线方程:
的切线斜率为K,则切线方程:

 (2分)
(2分)
 即
即
 (3分)
(3分)
 又
又



 (4分)
(4分)


 (5分)
(5分)
 ,
, 


 (6分)
(6分) 可得:
可得:




 (8分)
(8分) (9分)
(9分)






 (11分)
(11分) ,取 “=”,此时
,取 “=”,此时
 (12分)
(12分) ,
, 
 故
故
 即证
即证
 (
( )
(1分)
)
(1分)



 即:
即: (3分)
(3分)
 (
(





 (6分)
(6分)



 (8分)
(8分)



 (10分)
(10分)
 (11分)
(11分) (12分)
(12分)