长山中学2008级第二学期第一学段
数学试题
本试卷分第I卷(选择题)和第II卷(非选择题)两部分,第I卷第I至第2页,第II卷第3至第5页 全卷满分100分,考试时间90分钟
全卷满分100分,考试时间90分钟
一、选择题:本卷共15小题,每小题3分,共45分.在每小题给出的四个选项中,只有一项是符合题目要求的,请把符合要求的选项涂填在答题卡上.
1.已知数列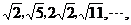 则
则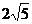 是这个数列的( )
是这个数列的( )
(A) 第六项 (B) 第七项 (C) 第八项 (D)第九项
2.等差数列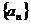 的前
的前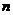 项和为
项和为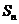 ,若
,若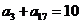 则
则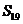 ( )
( )
(A) 55 (B)
3.在△ABC中,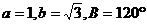 ,则A等于 ( )
,则A等于 ( )
(A)30° (B) 45° (C) 60° (D) 120°
4.在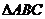 中,已知
中,已知 ,则
,则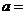 ( )
( )
(A)2; (B)1; (C)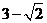 ; (D)
; (D)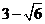 .
.
5.已知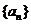 是公比为
是公比为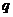 的等比数列,且
的等比数列,且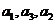 成等差数列,则
成等差数列,则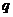 等于( )
等于( )
(A)1; (B)-2; (C)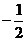 ; (D)1或
; (D)1或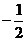 .
.
6.将9个数排成如下图所示的数表,若每行3个数按从左至右的顺序构成等差数列,每列的
3个数按从上到下的顺序也构成等差数列,且表正中间一个数a22=2,则表中所有数之和
为 ( )

(A) 20 (B) 18 (C) 512 (D) 不确定的数
7.在△ABC中,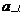
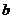
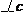 分别是∠A、∠B、∠C的对边,且
分别是∠A、∠B、∠C的对边,且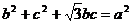 ,
,
则∠A等于( )
(A) 60° (B) 30° (C) 120° (D) 150°
8.在数列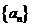 中,已知
中,已知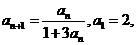 则
则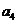 等于( )
等于( )
(A) 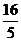 (B)
(B)
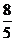 (C)
(C)
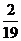 (D)
(D)
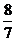
9.设 ,那么数列a、b、c是 ( )
,那么数列a、b、c是 ( )
(A) 是等差数列但不是等比数列 (B) 是等比数列但不是等差数列
(C) 既是等比数列又是等差数列 (D) 既不是等比数列又不是等差数列
11.某人朝正东方向走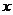 千米后,向右转
千米后,向右转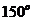 并走
并走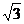 千米,
千米,
那么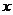 的值为 ( )
的值为 ( )
(A) 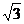 (B)
(B)
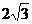 (C)
(C) 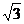 或
或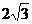 (D) 3
(D) 3
12.在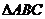 中,若
中,若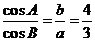 ,则
,则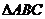 是 ( )
是 ( )
(A) 直角三角形 (B) 等腰三角形
(C) 等腰或直角三角形 (D) 钝角三角形
13.在△ABC中,若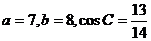 ,则最大角的余弦是(
)
,则最大角的余弦是(
)
(A) 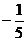 (B)
(B)
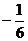 (C)
(C)
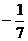 (D)
(D)
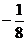
14.已知等比数列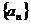 的前n项和为
的前n项和为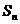 ,且
,且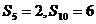 ,则
,则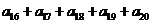
的值是 ( )
(A) 54 (B)
15.等差数列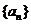 中,
中,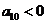 ,
,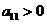 ,且
,且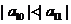 ,
,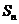 为其前
为其前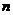 项之和,则( )
项之和,则( )
(A)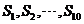 都小于零,
都小于零,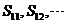 都大于零
都大于零
(B)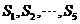 都小于零,
都小于零,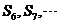 都大于零
都大于零
(C)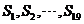 都小于零,
都小于零,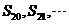 都大于零
都大于零
(D)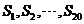 都小于零,
都小于零,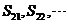 都大于零
都大于零
二、填空题:本大题共5小题,每小题4分,共20分
16.若数列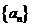 的前
的前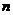 项和
项和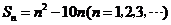 ,则此数列的通项公式为
,则此数列的通项公式为
17.在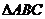 中,
中,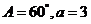 ,则
,则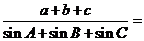
18.在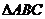 中,三个内角
中,三个内角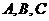 成等差数列,对应三边
成等差数列,对应三边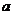 、
、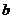 、
、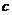 成等比数列,
成等比数列,
则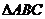 的形状是 .
的形状是 .
19.给定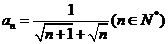 ,则使
,则使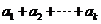 为整数的最小正整数
为整数的最小正整数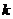 的值
的值
是
20.等差数列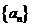 中,
中,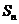 是它的前
是它的前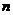 项之和,且
项之和,且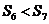 ,
,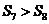 ,则
,则
①数列的公差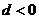 ②
②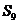 一定小于
一定小于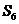
③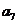 是各项中最大的一项 ④
是各项中最大的一项 ④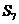 一定是
一定是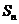 n中的最大值
n中的最大值
其中正确的是_______________________(填入你认为正确的所有序号).
21(本小题满分6分)
三、解答题(本大题共5小题,共35分。解答应写出文字说明、证明过程或演算步骤)
已知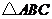 的周长为
的周长为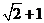 ,且
,且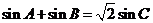 .
.
(I)求边 的长;
的长;
(II)若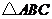 的面积为
的面积为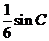 ,求角
,求角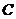 的度数.
的度数.
22.(本题满分7分)
已知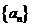 是等差数列,其中
是等差数列,其中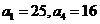
(Ⅰ)求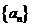 的通项;
的通项;
(Ⅱ)数列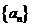 从哪一项开始小于0;
从哪一项开始小于0;
(Ⅲ)求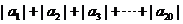 值。
值。
23(本题满分7分)
在△ABC中,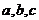 分别是
分别是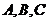 的对边,且
的对边,且

(Ⅰ)求角B的大小;
(Ⅱ)若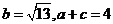 ,求
,求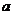 的值;
的值;
24.(本小题满分7分)
在等比数列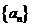 中,
中,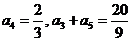 .
.
(I)求数列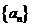 的通项公式;
的通项公式;
(II)若数列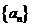 的公比大于
的公比大于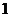 ,且
,且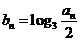 ,求数列
,求数列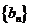 的前
的前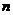 项和
项和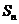 .
.
25(本题满分8分)
设{an}是正数组成的数列,其前n项和为Sn,并且对于所有的n 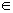 N+,都有
N+,都有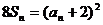 。
。
(Ⅰ)写出数列{an}的前3项;
(Ⅱ)证明数列{an}是等差数列,并求其通项公式(写出推证过程);
(Ⅲ)设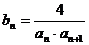 ,
,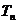 是数列{bn}的前n项和,求使得
是数列{bn}的前n项和,求使得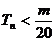 对所有n
对所有n 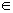 N+都成立的最小正整数
N+都成立的最小正整数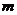 的值。
的值。
长山中学2008级第二学期第一学段
一、选择题
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
B
B
A
B
D
B
C
C
A
B
C
A
C
D
C
二、填空题
16. ;17.
;17. ;18等边三角形;19.3;20.①②④
;18等边三角形;19.3;20.①②④
三、解答题
21解(I)由题意及正弦定理,得 ①,
①,
 ②,………………1分
②,………………1分
两式相减,得 . …………………2分
. …………………2分
(II)由 的面积
的面积 ,得
,得 ,……4分
,……4分
由余弦定理,得
 ……………5分
……………5分
所以 . …………6分
. …………6分
22 .解:(Ⅰ)
 ……2分
……2分
(Ⅱ)

∴数列 从第10项开始小于0
……4分
从第10项开始小于0
……4分
(Ⅲ)




23解:(Ⅰ)由 得
得
即:
∴ …………2分
…………2分
而 又
又
而 …………4分
…………4分
(Ⅱ)利用余弦定理 可解得:
可解得:
 ,∵
,∵ ,故有
,故有 或
或 …………7分
…………7分
24解:(I)设等比数列{an}的公比为q, 则q≠0, a2= = , a4=a3q=2q
所以 + 2q= , 解得q1= , q2= 3, …………1分
当q1=, a1=18.所以 an=18×( )n-1= = 2×33-n.
当q=3时, a1=  ,所以an=
,所以an= ×
× =2×3n-5.
…………3分
=2×3n-5.
…………3分
(II)由(I)及数列 公比大于
公比大于 ,得q=3,an=2×3n-5 ,…………4分
,得q=3,an=2×3n-5 ,…………4分
 ,
,
 (常数),
(常数),  .
.
所以数列 为首项为-4,公差为1的等差数列,……6分
为首项为-4,公差为1的等差数列,……6分
 . …………7分
. …………7分
25.解:(Ⅰ) n=1时  ∴
∴
n=2时
 ∴
∴
n=3时
 ∴
∴ …………2分
…………2分
(Ⅱ)∵ ∴
∴
两式相减得:  即
即
也即
∵ ∴
∴ 即
即 是首项为2,公差为4的等差数列
是首项为2,公差为4的等差数列
∴ …………5分
…………5分
(Ⅲ)
∴
 …………7分
…………7分
∵ 对所有
对所有 都成立 ∴
都成立 ∴ 即
即
故m的最小值是10 …………8分
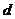 不为0,
不为0,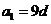

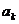 是
是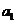 与
与 的等比中项,则
的等比中项,则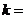 ( )
( )