济宁市高三数学
教研会
《2008年山东省数学高考考试说明》解读
李中华 马东亮
兖州实验高中
《2008年山东省数学高考考试说明》解读
一、08年山东省数学高考考试说明与07年考试说明的对比变化
所在位置
07年考试说明
08年考试说明
1
Ⅰ.命题指导思想
三、考试范围
2. 函数概念与基本初等函数I(指数函数、对数函数、幂函数)
(6)函数模型及其应用
① 了解指数函数、对数函数以及幂函数的增长特征;理解直线上升、指数增长、对数增长等不同函数类型增长的含义.
2. 函数概念与基本初等函数I(指数函数、对数函数、幂函数)
(6)函数模型及其应用
① 了解指数函数、对数函数以及幂函数的增长特征;知道直线上升、指数增长、对数增长等不同函数类型增长的含义.
5
13. 不等式
(1)不等关系
了解现实世界和日常生活中存在着大量的不等关系,了解不等式(组)的实际背景.
13. 不等式
(1)不等关系
了解现实世界和日常生活中的不等关系,了解不等式(组)的实际背景.
6
四、具体考试内容及其要求
14. 常用逻辑用语
(1)命题及其关系
①了解命题及其逆命题、否命题与逆否命题。
②理解必要条件、充分条件与充要条件的意义,会分析四种命题的相互关系.
14. 常用逻辑用语
(1)命题及其关系
①理解命题的概念.
②了解“若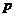 ,则
,则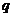 ”形式的命题的逆命题、否命题与逆否命题,会分析四种命题的相互关系.
”形式的命题的逆命题、否命题与逆否命题,会分析四种命题的相互关系.
③理解必要条件、充分条件与充要条件的意义.
7
21.概率与统计
(2)统计案例
了解下列一些常见的统计方法,并能应用这些方法解决一些实际问题.
① 独立性检验
了解独立性检验(只要求2×2列联表)的基本思想、方法及其简单应用.
② 假设检验
了解假设检验的基本思想、方法及其简单应用.
③聚类分析
了解聚类分析的基本思想、方法及其简单应用.
④回归分析
了解回归的基本思想、方法及其简单应用.
21.概率与统计
(2)统计案例
了解下列一些常见的统计方法,并能应用这些方法解决一些实际问题.
① 独立性检验
了解独立性检验(只要求2×2列联表)的基本思想、方法及其简单应用.
② 假设检验
了解假设检验的基本思想、方法及其简单应用.
③ 回归分析
了解回归的基本思想、方法及其简单应用.
(删掉③聚类分析)
8
22.不等式的基本性质和证明的基本方法
(1)理解绝对值的几何意义,并能利用含绝对值不等式的几何意义证明以下不等式:
① 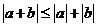 .
.
② 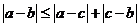 .
.
(2)会利用绝对值的几何意义求解以下类型的不等式:
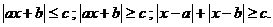 (3)了解证明不等式的基本方法:比较法、综合法、分析法.
(3)了解证明不等式的基本方法:比较法、综合法、分析法.
9
Ⅳ.题型示例
(置 换)
0
(文科)
7. 概率
(2)古典概型
② 会计算一些随机事件所含的基本事件数及事件发生的概率.
7. 概率
(2)古典概型
② 会用列举法计算一些随机事件所含的基本事件数及事件发生的概率.
二、《2008年山东省数学高考考试说明》解读
1.函数与导数:高中数学的主线,高考试卷的骨架,把关题首选.其中函数的图像及其基本性质、几种特殊函数类型、“三个二次”的有关问题和解法、函数与方程、分类与整合、数形结合以及转化与化归的数学思想方法等应得到重视.
• 重点:函数的图象及性质;单调性;幂函数 ;函数与方程(零点)和二分法
• “三个二次”及方法 :掌握求解含参数的二次函数在区间[m,n]上的最值问题;
• 掌握求解含参数的二次不等式在R或R的子集上恒成立的问题;
• 掌握求解含参数的二次函数在区间[m,n]上的零点个数问题。
2.算法与框图:新课标新增主要内容之一,掌握一种简化问题的方法.重点在算法与框图,淡化语言.
3.推理与证明:新课标新增主要内容之一,重点是合情推理问题,体现和培养创新意识,可能是08年高考数学命题的一个热点.高中数学的通性通法是高考数学命题的支点和落脚点.
直接证明的逻辑方法 :比较法、分析法、综合法、类比法、归纳法、放缩法等 ;
间接证明的逻辑方法:反证法 。
4.立体几何:文科考生在考试内容和要求上变化最大的一部分.有淡化、有提升,更加侧重几何直观能力.注意理解课标和考钢中的“四个画出”,提高“识图、想图、画图”的能力.
重视几何直观能力 ;探究与证明的能力
5.解析几何:典型的传统内容,但是整体要求降低.重点在椭圆.许多隐含的边缘问题值得探究.
6.数列:高等数学与初等数学的重要结合点,也是高考数学命题持续的热点,重点是两个基本数列和数列的两个基本问题.递推关系的“淡出”引起不同的理解.注意归纳与猜想的推理方法,侧重转化与化归的数学思想.
7.三角函数与向量:继承课改的变化和要求,考试的范围和要求变化不大.向量的基本定理和基本运算的应用是重点. 向量的数量积运算是难点.注意函数(不仅限于三角函数)图像变换和性质以及正弦、余弦定理的应用,体现“三维目标”和研究性学习.
8.应用问题(含概率统计):新课标的主要特色之一,体现“三维目标”和实践能力.以概率统计(理科)、函数(文科)为平台,注意随机数、几何概型、三个概率分布、回归分析和简单的定积分运算等新增的几个“小问题”.
• 随机抽样;独立检验;回归分析 ;统计思维与确定性思维;随机数与几何概型 ;三个分布。
9.不等式选修有关问题:大部分已复习,一定要有所体现。
10.正确看待“题型示例”
《说明》中所提供的“题型示例”主要是告诉考生的题目类型、题目的大致难度,而非2008年高考数学试题的模板,切忌对号入座,机械模仿练习。
11.高中数学蕴含的七种数学思想方法
数形结合的思想方法; 函数与方程的思想方法;分类与整合的思想方法;转换与化归的思想方法
特殊与一般的思想方法;有限与无限的思想方法;或然与必然的思想方法
12.常见的解题方法
配方法、换元法、坐标法、消元法、二分法、最小二乘法、五点作图法、割补法、等积法、导数法、待定系数法、数学归纳法等
波浪线法、射影法、放缩法、判别式法、构造法、点差法、交轨法、迭代(倒推)法、累加与累乘法、错项法、裂项法、切化弦、角的变换等
三、计算机网上阅卷
前些天,省考试院命制了一份计算机网上阅卷的模拟试题,在个别地区进行了一次模拟考试,大约有五万考生参加。11-16号在山东大学就以这五万份试卷模拟网上阅卷的过程,参加这次阅卷的老师大约有200人。为六月份正式施行网上阅卷积累经验。首先培训省质检组成员、大组长和部分小组长30余人,熟悉数学答题卡的格式,了解数学网上阅卷程序和要求。在试评的过程中,发现了不少问题。考生方面:主要是答题位置写错,张冠李戴;阅卷方面:评分误差如何更有效的控制、避免漏评等。
4.计算机网上阅卷的数学试卷的格式
分试题纸和答题纸。试题纸一张(根据情况),题目之间不留空。答题纸两张,第一张的左边开始是考生的信息,然后是选择题和填空题的答案栏,下面和右边是第17题的答题位置,反面的左边是第18题的答题位置,反面的右边是第19题的答题位置。第二页答题纸,分别是第20、21和22题的答题位置。
四、对高考数学复习的建议
1.高考大纲和说明是命题的依据
避免教学与高考“死挂勾”,高考与教学总是密切联系又具有一定的相互独立性。因此,教学既要受高考的影响,又要保持自己的独立品格,不仅要教高考能考出来的东西,也要教高考可能考查不出但对学生素质发展非常重要的数学内容。总之,在教学及复习中,希望广大教师要正确处理《标准》、教材与《说明》的关系。
2.主干知识和方法是试卷的骨架
突出知识结构,扎扎实实打好基础 ,要提醒学生,数学知识结构的形成和发展是一个知识积累、梳理的过程,教学复习中首先要扎扎实实学好基础知识,并在此基础上,注意各部分知识在各自发展过程中的纵向联系,以及各部分知识之间的横向联系,理清脉络,抓住主干知识,构建知识网络。在总复习中要充分重视主干知识的支撑作用,通过抓主干知识,带动基础,促进全面,而抓好基础,搞好落实,是提高能力的保障。因此抓基础是我们复习教学工作的重中之重。
强化思维过程,努力提高理性思维能力 ,数学基础知识的学习要充分重视知识的形成过程,解数学题要着重研究解题的思维过程,弄清基本数学方法和基本数学思想在解题中的意义和作用,研究运用不同的思维方法解决同一个数学问题的多条途径,注意培养直觉猜想、归纳抽象、逻辑推理、演绎证明、运算求解等理性思维能力。近几年高考阅卷可以看到一个比较突出的现象是,学生的运算能力普遍下滑,导致许多问题的解答半途而废。这里面有各方面的原因,如计算器和计算机的普及,造成学生包括教师主观上对运算能力要求的降低。需要指出的是,作为数学学科对运算能力的要求不同于理化学科,并不是侧重于数值运算能力的高低,而是强调字符和代数式的化简以及运算律的熟练运用。在某种意义上说,数学运算能力也是数学思维能力的一个重要方面。数学思维能力是在知识传授和学习过程中逐渐得到培养和发展的,需要教师正确地开发和引导.从高考改革的趋势来看,将来的高考试题会给思维能力强的学生留下了充分施展才能的空间。
3.应用和探究是新课改试题的特色
4.能力和创新是新课程高考的主题
增强实践意识,重视应用意识和创新意识的培养 课程改革对数学知识的应用提出了更高的要求:高中数学课程对于认识数学与自然界、数学与人类文化的关系,认识数学的科学价值、文化价值,提高提出问题、分析问题和解决问题的能力,形成理性思维,发展智力和创新意识具有基础性的作用。高中数学课程有助于认识数学的应用价值,增强应用意识,形成解决简单实际问题的能力。课程的基本理念之一是发展学生的数学应用意识。因此在复习中要善于把实际问题与所学的数学知识联系起来,其实前几年的应用题也是从学生身边熟悉的问题,如社会热点、重大事件、环境问题、新科技、生活常识等问题切入。所以教学中要把培养学生的创新意识和实践能力作为基本目标,鼓励学生独立思考,增强用数学的意识,逐步学会用已有的数学知识去探索新的数学问题,学会将实际问题抽象转化为数学问题,并加以解决。