安徽省马鞍山二中2009年四模考试
数学(理科)试题
第Ⅰ卷(共60分)
一.选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.
1.设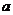 是实数,且
是实数,且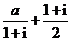 是纯虚数,则
是纯虚数,则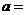
A.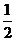 B.
B.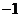 C.
C.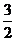 D.
D.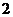
2.已知命题 所有的有理数都是实数,命题
所有的有理数都是实数,命题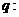 正数的对数都是负数,则下列命题中为真的是
正数的对数都是负数,则下列命题中为真的是
A.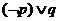 B.
B.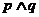 C.
C.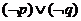 D.
D.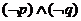
 3.若
3.若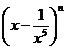 的展开式中不含有常数项,那么
的展开式中不含有常数项,那么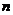 的取值可以是
的取值可以是
A.6 B.8 C.12 D.18
4.设等比数列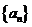 的公比q=2,前n项和为Sn,则
的公比q=2,前n项和为Sn,则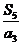 =
=
A.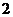 B.
B.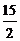 C.
C.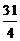 D.
D.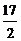
5.已知三个实数a,b,c表示三条曲线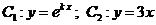
|
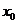 是
是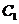 在
在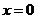 处的切线斜率,那么
处的切线斜率,那么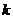 的范围是
的范围是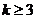 B.
B.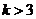 C.
C.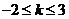 D.
D.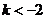
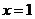 ,x=2,曲线
,x=2,曲线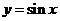 及x轴所围图形的面积为
及x轴所围图形的面积为
 B.
B.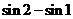
 D.
D.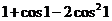
 7.已知曲线C1:
7.已知曲线C1: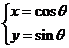 (
(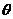 为参数),曲线C2:
为参数),曲线C2: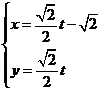 (t为参数).则曲线C1与曲线C2的交点个数为
(t为参数).则曲线C1与曲线C2的交点个数为
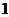 D.
D.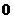
 B.
B.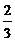
 9.如图,虚线部分是四个象限的角平分线,实线部分是函数
9.如图,虚线部分是四个象限的角平分线,实线部分是函数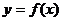 的部分图像,则
的部分图像,则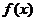 可能是
可能是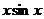 B.
B.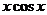 C.
C.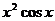 D.
D.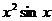
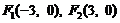 是椭圆
是椭圆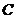 的两个焦点,若直线
的两个焦点,若直线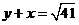 与椭圆
与椭圆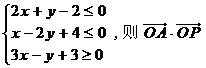 最小值是
最小值是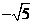 C.
C.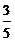 D.
D.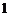
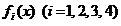 是定义在[0,1]上的四个函数,其中满足性质:“对[0,1]中任意的
是定义在[0,1]上的四个函数,其中满足性质:“对[0,1]中任意的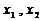 和任意
和任意 恒成立”的只有
恒成立”的只有 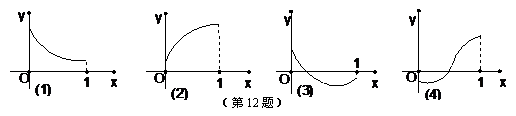
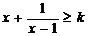 恒成立,则实数k的取值范围是
恒成立,则实数k的取值范围是
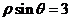 ,曲线
,曲线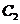 的极坐标方程为
的极坐标方程为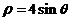 (
(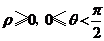 ),则曲线
),则曲线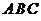 三边长为
三边长为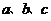 ,与之对应的三条高分别为
,与之对应的三条高分别为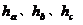 ,若满足关系:
,若满足关系: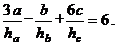
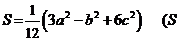 是△
是△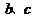 表示
表示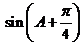 ,并求出角
,并求出角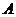 的大小.
的大小.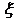 为两枚骰子的点数之和.
为两枚骰子的点数之和.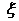 的分布列.
的分布列.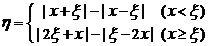 ,求
,求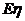 的最大值(其中
的最大值(其中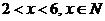 )
)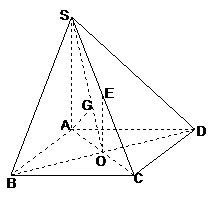 已知四棱锥
已知四棱锥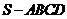 的底面
的底面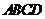 是正方形,侧棱
是正方形,侧棱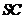 的中点
的中点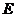 在底面内的射影恰好是正方形
在底面内的射影恰好是正方形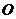 ,顶点
,顶点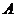 在截面
在截面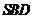 内的射影恰好是
内的射影恰好是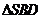 的重心
的重心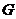 .
.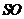 与底面
与底面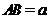 ,求此四棱锥过点
,求此四棱锥过点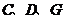 的截面面积.
的截面面积.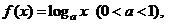 若数列{a n}满足:
若数列{a n}满足: 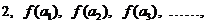
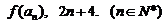 成等差数列.
成等差数列.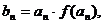 若{b n}的前n项和是S n,且
若{b n}的前n项和是S n,且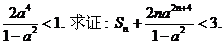
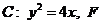 是
是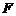 的直线
的直线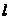 与
与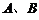 两点.
两点.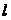 的斜率为1,求
的斜率为1,求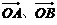 夹角的余弦值;
夹角的余弦值;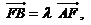 若
若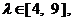 求直线
求直线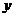 轴上截距的变化范围.
轴上截距的变化范围.
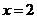 处的切线方程为
处的切线方程为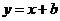 ,求
,求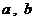 的值;
的值;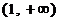 上是增函数,求实数
上是增函数,求实数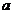 的取值范围;
的取值范围;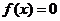 解的个数,并说明理由.
解的个数,并说明理由. 14.
14. 15.
15. 16.
16. (万元)
(万元)
 得:
得:
 (5分)
(5分)
 由余弦定理得:
由余弦定理得:

 -----------------------------
(9分)
-----------------------------
(9分)


 ------ (12分)
------ (12分) 的分布列.
的分布列. 




 为事件
为事件
 ,同掷出2的概率
,同掷出2的概率 ,同掷出3的概率
,同掷出3的概率


 (8分)
(8分)

 时)
时)
 =
=
 时)
时)
 时)
时)
 时,
时,  (12分)
(12分)


 两两相互垂直, 连结
两两相互垂直, 连结 并延长交
并延长交 于F.
于F.





 ------------ (6分)
------------ (6分) 是
是 的重心
的重心


 --- (12分)
--- (12分) d=2,
d=2,
 ……………………(4分)
……………………(4分) ,
,

 --------------------
(8分)
--------------------
(8分) 


 的斜率为1,抛物线
的斜率为1,抛物线 的焦点
的焦点







 夹角的余弦值为
夹角的余弦值为 ----------------- (6分)
----------------- (6分)



 在
在 轴上截距为
轴上截距为 或
或
 是
是 的减函数
的减函数 从而得
从而得

 ------------ (12分)
------------ (12分)
 在直线
在直线 上,
上,

 在
在 上是增函数,
上是增函数, 在
在 ??????????????? (8分)
??????????????? (8分) ,
, 时,
时, 在
在 ,
, 无解;
无解; 时,
时, 在
在 ,
, 有唯一解;
有唯一解; 时,
时,
 上
上 上
上
 时,
时, 无解;
无解; 时,
时, ;
; 时,
时,
 上,
上, 有唯一解
有唯一解 上,设
上,设


 上,
上, 时,
时,
 时,
时,