山东省乐陵一中2009届高三考前回扣45分钟练习六
解析几何
一、选择题
1、“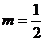 ”是“直线
”是“直线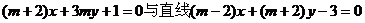 互相
互相
垂直”的 ( ).
A.充分而不必要条件 B.必要而不充分条件
C.充要条件 D.既不充分也不必要条件
2、已知抛物线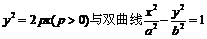
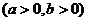 有相同的焦点F,点A是两曲线的交点,且AF⊥
有相同的焦点F,点A是两曲线的交点,且AF⊥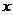 轴,则双曲线的离心率为
( ).
轴,则双曲线的离心率为
( ).
A.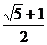 B.
B.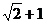 C.
C.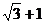 D.
D.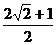
3、如果点P到点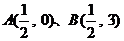 及直线
及直线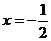 的距离都相等,那么满足条件的点P的个数有
( )
的距离都相等,那么满足条件的点P的个数有
( )
A.0个 B.1个 C.2个 D.无数个
4、设双曲线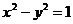 的两条渐近线与直线
的两条渐近线与直线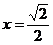 围成的三角形区域(包括边界)为E,
围成的三角形区域(包括边界)为E,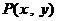 为该区域内的一动点,则目标函数
为该区域内的一动点,则目标函数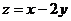 的最小值为 ( )
的最小值为 ( )
A.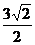 B.
B.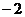 C.0 D.
C.0 D.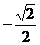
5、过双曲线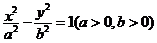 的左焦点F1,作圆
的左焦点F1,作圆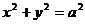 的切线交双曲线右支于点P,切点为T,PF1的中点M在第一象限,则以下正确的是 ( )
的切线交双曲线右支于点P,切点为T,PF1的中点M在第一象限,则以下正确的是 ( )
A.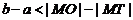 B.
B.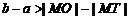
C.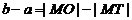 D.
D.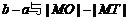 大小不定
大小不定
6、已知直线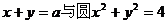 交于A、B两点,且
交于A、B两点,且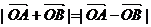 ,其中O为原点,则实数
,其中O为原点,则实数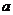 的值为
( 0
的值为
( 0
A.2
B.-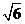 或
或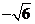
二、填空题
7、将抛物线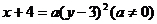 按向量v=(4,-3)平移后所得抛物线的焦点坐标为
.
按向量v=(4,-3)平移后所得抛物线的焦点坐标为
.
8、已知F1、F2是椭圆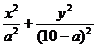 =1(5<a<10=的两个焦点,B是短轴的一个端点,则△F1BF2的面积的最大值是
=1(5<a<10=的两个焦点,B是短轴的一个端点,则△F1BF2的面积的最大值是
9、已知抛物线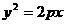
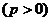 ,过点
,过点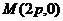 的直线与抛物线相交于
的直线与抛物线相交于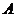 ,
,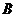 ,
,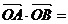 .
.
三、解答题
10、若双曲线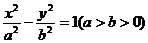 的左右焦点分别为
的左右焦点分别为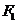 、
、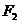 ,线段
,线段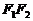 被抛物线
被抛物线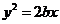 的焦点分成
的焦点分成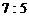 的两段,则此双曲线的离心率为
的两段,则此双曲线的离心率为
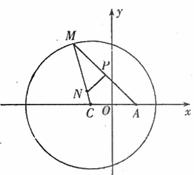
11、如图所示,已知圆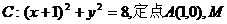 为圆上一动点,点P在AM上,
为圆上一动点,点P在AM上,
点N在CM上,且满足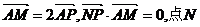 的轨迹为曲线E.
的轨迹为曲线E.
(I)求曲线E的方程;
(II)若过定点F(0,2)的直线交曲线E于不同的两点G、H(点G在点F、H之间),
且满足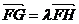 ,求
,求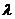 的取值范围.
的取值范围.
12、设椭圆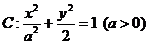 的左、右焦点分别为
的左、右焦点分别为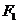 、
、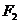 ,A是椭圆C上的一点,且
,A是椭圆C上的一点,且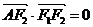 ,坐标原点O到直线
,坐标原点O到直线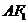 的距离为
的距离为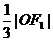 .
.
(1)求椭圆C的方程;
(2)设Q是椭圆C上的一点,过Q的直线l交x轴于点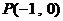 ,较y轴于点M,若
,较y轴于点M,若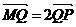 ,求直线l的方程.
,求直线l的方程.
1、A 2、B 3、B 4、D 5、C 6、C
 7、
7、 8、
8、 9、0
10、
9、0
10、
11、【解】(1)
∴NP为AM的垂直平分线,∴|NA|=|NM|.…………………………2分
又
∴动点N的轨迹是以点C(-1,0),A(1,0)为焦点的椭圆.
且椭圆长轴长为 焦距
焦距 ……………5分
……………5分
∴曲线E的方程为 ………………6分
………………6分
(2)当直线GH斜率存在时,
设直线GH方程为
得
设 ……………………8分
……………………8分

 ,
,
 ……………………10分
……………………10分


又当直线GH斜率不存在,方程为
 ……………………………………12分
……………………………………12分
12、【解】(1)由题设知
由于 ,则有
,则有 ,所以点A的坐标为
,所以点A的坐标为 ,
,
故 所在直线方程为
所在直线方程为 ,
………………………………3分
,
………………………………3分
所以坐标原点O到直线 的距离为
的距离为 ,
,
又 ,所以
,所以 ,解得
,解得 ,
,
所求椭圆的方程为 .……………………………………………5分
.……………………………………………5分
(2)由题意知直线l的斜率存在,设直线l的方程为 ,则有
,则有 ,
,
设 ,由于
,由于 ,
,
∴ ,解得
,解得 …………………8分
…………………8分
又Q在椭圆C上,得 ,
,
解得 ,
…………………………………………………………………………10分
,
…………………………………………………………………………10分
故直线l的方程为 或
或 ,
,
即 或
或 . ……………………………………………12分
. ……………………………………………12分