山东省乐陵一中2009届高三考前回扣45分钟练习八
统计与概率、计数原理
一、选择题
1、在某次数学测验中,学号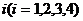 的四位同学的考试成绩
的四位同学的考试成绩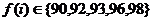 ,
且满足
,
且满足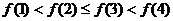 ,则这四位同学的考试成绩的所有可能情况的种数为 ( )
,则这四位同学的考试成绩的所有可能情况的种数为 ( )
A.9种 B.5种 C.23种 D.15种
2、两位大学毕业生一起去一家单位应聘,面试前单位负责人对他们说:“我们要从面试的人中招聘3人,你们俩同时被招聘进来的概率是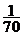 ”,根据这位负责人的话可以推断出参加面试的人数为
(
)
”,根据这位负责人的话可以推断出参加面试的人数为
(
)
A.21 B.
3、一块各面均涂有油漆的正方体被锯成1000个大小相同的小正方体,若将这些小正方体均匀地搅混在一起,则任意取出一个正方体其两面涂有油漆的概率是 ( )w.w.w.k.s.5.u.c.o.m
A.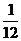 B.
B.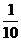 C.
C.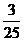 D.
D.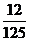
4、下列命题中,其中假命题是 ( )
A.对分类变量X与Y的随机变量K2的观测值k来说,k越小,“X与Y有关系”可信程度越大
B.用相关指数R2来刻画回归的效果时,R2的值越大,说明模型拟合的效果越好
C.两个随机变量相关性越强,则相关系数的绝对值越接近1
D.三维柱形图中柱的高度表示的是各分类变量的频数
5、用4种不同的颜色为正方体的六个面着色,要求相邻两个面颜色不相同,则不同的着色方法有 种。 ( )
A.24
B.
6、在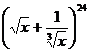 的展开式中,x的幂指数是整数的项共有 ( )
的展开式中,x的幂指数是整数的项共有 ( )
A.3项 B.4项 C.5项 D.6项
二、填空题
7、一个总体依有100个个体,随机编号0,1,2,…,99,依从小到大的编号顺序平均分成10个小组,组号依次为1,2,3,…,10,现用系统抽样方法抽取一个容量为10的样本,规定如果在第1组随机抽取的号码为m,那么在第k组中抽取的号码个位数字与m+k的个位数字相同,若m=8,则在第8组中抽取的号码是________.
8、 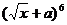 的展开式中x2项的系数为60,则实数a= .
的展开式中x2项的系数为60,则实数a= .
9、学校为了调查学生在课外读物方面的支出情况,抽出了一个容量为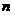 的样本,其频率分布直方图如图所示,其中支出在
的样本,其频率分布直方图如图所示,其中支出在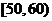 元的同学有
元的同学有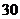 人,则
人,则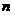 的值为
的值为

10、设函数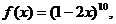 则导函数
则导函数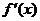 的展开式
的展开式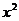 项的系数为
项的系数为
三、解答题
11、甲、乙两人进行射击训练,命中率分别为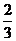 与P,且乙射击2次均未命中的概率为
与P,且乙射击2次均未命中的概率为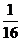 ,
,
(I)求乙射击的命中率;
(II)若甲射击2次,乙射击1次,两人共命中的次数记为ξ,求ξ的分布列和数学期望。
12、甲、乙两艘轮船驶向一个不能同时停泊两艘轮船的码头,它们在一昼夜内任何时刻到达是等可能的.
(1)如果甲船和乙船的停泊时间都是4小时,求它们中的任何一条船 不需要等等码头空出的概率;
(2)如果甲船的停泊时间为4小时,乙船的停泊时间是2小时,求它们中的任何一条船 不需要等待码头空出的概率.
1、D 2、A 3、D 4、A 5、D 6 、C
7、76 8、 9、
9、 10、 -2880
10、 -2880
11、解:(I)设“甲射击一次命中”为事件A,“乙射击一次命中”为事件B
由题意得 ┉┉┉┉┉┉┉┉┉┉4分
┉┉┉┉┉┉┉┉┉┉4分
解得 或
或 (舍去),┉┉┉┉┉┉┉┉┉┉5分
(舍去),┉┉┉┉┉┉┉┉┉┉5分
故乙射击的命中率为 。┉┉┉┉┉┉┉┉┉┉6分
。┉┉┉┉┉┉┉┉┉┉6分
(II)由题意和(I)知 。
。
ξ可能的取值为0,1,2,3,故
 ┉┉┉┉┉┉┉┉┉┉7分
┉┉┉┉┉┉┉┉┉┉7分
 .8分
.8分
 ┉┉┉┉┉┉┉┉┉┉9分
┉┉┉┉┉┉┉┉┉┉9分
 ┉┉┉10分
┉┉┉10分
故ξ的分布列为
ξ
0
1
2
3
P




由此得ξ的数学期望 ┉┉┉12分
┉┉┉12分
12、【解】(1)设甲、乙两船到达时间分别为x、y,则O≤x<24,0≤y<24且y-x>4或y-x<-4
作出区域 4分
4分
设“两船无需等待码头空出”为事件A,则
P(A)= 6分
6分
(2)当甲船的停泊时间为4小时,两船不需等待码头空出,则满足x-y>2. 8分
 10分
10分
P(B)= 12分
12分
