湖北省武汉市武昌区 2009届高三年级五月调研测试
文 科 数 学 试 卷
2009.5.21
本试卷满分150分,考试用时120分钟.
注意事项:
1.答卷前,考生务必将自已的姓名、准考证号填写在试题卷和答题卡上,并将准
考证号条形码粘贴在答题卡上的指定位置。
2.选择题选出答案后,有2B铅笔把答题卡上对应题目的答案标号涂黑。如需改
动,橡皮擦干净后,再选涂其他答案标号。非选择题用黑色墨水的签字笔直接答在答
题卡上。答在试题卷上无效。
参考公式:
如果事件A、B互斥,那么
如果事件A、B相互独立,那么
如果事件A在一次试验中发生的概率是 ,那么n次独立重复试验中恰好发生k次的概率
,那么n次独立重复试验中恰好发生k次的概率
球的表面积公式 ,其中
,其中 表示球的半径
表示球的半径
球的体积公式 ,其中
,其中 表示球的半径
表示球的半径
一.选择题:本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的.
1.“ ”是“
”是“ ,
, ”的( )
”的( )
A.充要条件 B.必要不充分条件
C.充分不必要条件 D.既不充分也不必要条件
2.已知I为实数集,集合 ,则
,则 =( )
=( )
A. B.
B. C.
C. D.
D.
3.已知数列{ }的各项均为正数,
}的各项均为正数, ,点
,点 在抛物线
在抛物线 上,则过点P(
上,则过点P( ,
,
 )和Q(
)和Q( +2,
+2,  )(n∈
)(n∈ )的直线的一个方向向量的坐标可以是( )
)的直线的一个方向向量的坐标可以是( )
A.(2, ) B.(-1,-1) C.(-
) B.(-1,-1) C.(- ,-1) D.(-
,-1) D.(- ,-2)
,-2)
4.直线 (
( 为实数)与圆
为实数)与圆 的位置关系为( )
的位置关系为( )
A.相交 B.相切 C.相离 D.不确定
5. 展开式的各项系数和大于8且小于32,则展开式中系数最大的项是(
)
展开式的各项系数和大于8且小于32,则展开式中系数最大的项是(
)
A. B.
B. C.
C. D.
D. 或
或
6.在等比数列 中,
中, ,且
,且 ,则
,则 =( )
=( )
A.16 B.27 C.36 D.81
7.已知三条不同的直线 、
、 、
、 ,两个不同平面
,两个不同平面 、
、 . 有下列命题:
. 有下列命题:
①

 ,
,

 ,
, ∥
∥ ,
, ∥
∥ ,则
,则 ∥
∥ ;
;
②若

 ,
,

 ,
, ⊥
⊥ ,
, ⊥
⊥ ,则
,则 ⊥
⊥ ;
;
③若 ⊥
⊥ ,
, ⊥
⊥ ,
, ⊥
⊥ ,则
,则 ⊥
⊥ ;
;
④若 ∥
∥ ,
,

 ,
,

 ,则
,则 ∥
∥ .
.
其中正确的命题是( )
A.①③ B.②④ C.①② D.③④
8.正四面体的四个面上分别写有1,2,3,4,将3个这样均匀的四面体同时投掷于桌面上,则与桌面接触的三个面上的数字的乘积能被3整除的概率为( )
A. B.
B. C.
C. D.
D.
9.函数 的图象是中心在原点,焦点在
的图象是中心在原点,焦点在 轴上,且长轴长为4,短轴长为2的椭圆在一、三象限内的两段弧,则不等式
轴上,且长轴长为4,短轴长为2的椭圆在一、三象限内的两段弧,则不等式 <
< +
+ 的解集为( )
的解集为( )
A.{ |
| <
< <0,或
<0,或 <
<
 2}
2}
B.{ |-2≤
|-2≤ <
< ,或
,或 <
< ≤2}
≤2}
C.{ |-2≤
|-2≤ <
< ,且
,且 ≠0}
≠0}
D.{ |-2≤
|-2≤ <
< ,或
,或 <
< ≤2}
≤2}
10.不等式组 所确定的平面区域记为D,若圆O:
所确定的平面区域记为D,若圆O: 上的所有点都在区域D内,则圆O的面积的最大值是( )
上的所有点都在区域D内,则圆O的面积的最大值是( )
A. B.
B. C.
C.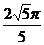 D.
D. 
二.填空题:本大题共5小题,每小题5分,共25分.把答案填在答题卡相应位置上.
11.双曲线 的焦点坐标为
.
的焦点坐标为
.
12.一样本的所有数据分组及频数如下:
 ―0.5,0.5),
―0.5,0.5),
 0.5,1.5),
0.5,1.5),
 1.5,2.5),
1.5,2.5),

 2.5,3.5),
2.5,3.5),
 3.5,4.5),
3.5,4.5),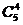
 4.5,5.5),
4.5,5.5),
则某数据在 1.5,4.5)内的频率为
.
1.5,4.5)内的频率为
.
13.如图,在半径为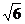
 ,圆心角为60°的扇形OAB中,点C为弧AB的中点,按如图截出一个内接矩形,则矩形的面积为
.
,圆心角为60°的扇形OAB中,点C为弧AB的中点,按如图截出一个内接矩形,则矩形的面积为
.
14.设函数 ,若
,若 时,
时, 恒成立,则实数
恒成立,则实数 的取值范围是_____________.
的取值范围是_____________.
15.直三棱柱ABC―A1B ,BC=C
,BC=C
三.解答题:本大题共6小题,共75分,解答应写出文字说明,证明过程或演算步骤.
16.(本小题满分12分)
已知 ,
, ,其中
,其中 ,设函数
,设函数
 .
.
(1)求函数 的值域;
的值域;
(2)若 ,求
,求 的值.
的值.
17.(本小题满分12分)如图所示,在直角梯形ABCP中,AP//BC,AP AB, AB=BC=
AB, AB=BC= ,D是AP的中点,E,F,G分别为PC、PD、CB的中点,将
,D是AP的中点,E,F,G分别为PC、PD、CB的中点,将 沿CD折起,使得
沿CD折起,使得 平面ABCD.
平面ABCD.
(1)求证:AP//平面EFG;
 (2)求二面角
(2)求二面角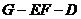 的大小.
的大小.
18. (本小题满分12分)
某公司的“咨询热线”电话共有6条外线,经长期统计发现,每天在电话高峰期,外线同时打入的概率如下表(记电话同时打入数为 ):
):

0
1
2
3
4
5
6
P
0.13
0.35
0.27
0.14
0.08
0.02
0.01
如果公司只安排两位接线员(一位接线员一次只能接一个电话).
(1)求每天电话高峰期内至少有一个电话不能一次接通的概率(用最简分数表示);
(2)公司董事会决定,把“一周五个工作日中至少有四天在电话高峰期内电话都能一次接通”的概率视作公司的“美誉度”,如果“美誉度”低于0.8,就增派接线员,请你帮助计算一下,该公司是否需要增派接线员?
19.(本小题满分12分)
已知函数 的导函数
的导函数 .
.
⑴ 求函数 的单调区间;
的单调区间;
⑵ 若 在区间
在区间 ,
, 上的最大值为20,求它在该区间上的最小值.
上的最大值为20,求它在该区间上的最小值.
20.(本小题满分13分)
已知椭圆 的中心、上顶点、右焦点构成面积为1的等腰直角三角形.
的中心、上顶点、右焦点构成面积为1的等腰直角三角形.
(1)求椭圆的方程;
(2)若A、B分别是椭圆的左、右顶点,点M满足MB⊥AB,连接AM,交椭圆于P点,试问:在 轴上是否存在异于点A的定点C,使得以MP为直径的圆恒过直线BP、MC的交点,若存在,求出C点的坐标;若不存在,说明理由.
轴上是否存在异于点A的定点C,使得以MP为直径的圆恒过直线BP、MC的交点,若存在,求出C点的坐标;若不存在,说明理由.
21.(本小题满分14分)
已知函数 ,M(
,M( ,
, )、N(
)、N(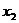 ,
, )是
)是 图象上的两点,横坐标为
图象上的两点,横坐标为 的点P满足
的点P满足
 =
= +
+ (O为坐标原点).
(O为坐标原点).
⑴ 求证: +
+ 为定值;
为定值;
⑵ 若 +
+ +…+
+…+ ,其中
,其中 ,且
,且 ≥2,求
≥2,求 ;
;
⑶ 已知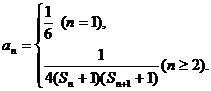 其中
其中 ,
, 为数列{
为数列{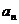 }的前n项和,若
}的前n项和,若 <
< 对一切
对一切 都成立,试求m的取值范围.
都成立,试求m的取值范围.

 又在三角形PAC中,E,O分别为PC,AC的中点,
又在三角形PAC中,E,O分别为PC,AC的中点, PA//EO.
PA//EO.
 平面EFOG,PA
平面EFOG,PA 平面EFOG,
平面EFOG,
 PA//平面EFOG,即PA//平面EFG. ………………
PA//平面EFOG,即PA//平面EFG. ………………
…………………………6分
方法二:连AC,BD交于O点,连GO,FO,EO.
∵E,F分别为PC,PD的中点,∴ //
// ,
,
同理 //
//
又 //AB,
//AB, //
// .
.
 平面EFG//平面PAB.
平面EFG//平面PAB.
又PA 平面PAB,
平面PAB, 平面EFG.…………………………………………6分
平面EFG.…………………………………………6分
(2)取AD的中点H,连结GH,则由 知平面EFG即为平面EFHG。
知平面EFG即为平面EFHG。

∴ 的单调减区间为
的单调减区间为 和
和 ,单调增区间为
,单调增区间为 . …………4分
. …………4分
(2)设 ,则
,则 .
.
∴3 =
―3,2
=
―3,2 =6,
=6, =9,即
=9,即 = ―1,
= ―1, =3,
=3, =9.
=9.
故 .
………………………………………………8分
.
………………………………………………8分
由⑴ 知 在
在 上单调递减,在
上单调递减,在 上单调递增.
上单调递增.
又 >
> =2+
=2+ ,
,
∴ .
.

所以 在
在 上的最小值为
上的最小值为 . ………………………………12分
. ………………………………12分
20.解:(1)由题意知 解得
解得 ,从而
,从而 .
.

21.解:(1)由已知可得 , ∴P是MN的中点,有
, ∴P是MN的中点,有 +
+ =1.
=1.
从而 +
+ =
= +
+ =
=
= 为定值. ………………………………………4分
为定值. ………………………………………4分
(2)由⑴ 知当 +
+ =1时,
=1时, +
+ =
= +
+ =1.
=1.

 +
+ +…+
+…+ ,
①
,
①
又
 +…
+… +
+  ,
②
,
②
① + ② 得 ,故
,故 .…………………………………8分
.…………………………………8分
(3)当 ≥2时,
≥2时, .
.
