2008――2009学年高三第一次调考理科数学试卷
考试时间120分钟 总分150分
一.选择题(本大题12小题,每小题5分,共60分)
1.复数 的虚部是
的虚部是
A. B.
B.
2.复数 ,则在复平面上,
,则在复平面上, 对应的点在
对应的点在
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.某商场有四类食品,其中粮食类、植物油类、动物性食品类及果蔬类分别有40种、10种、30种、20种,现从中抽取一个容量为20的样本进行食品安全检测.若采用分层抽样的方法抽取样本,则抽取的植物油类与果蔬类食品种数之和是
A.4 B.
4.某个命题与正整数有关,若当 时该命题成立,那么可推得当
时该命题成立,那么可推得当
 时该命题也成立,现已知当
时该命题也成立,现已知当 时该命题不成立,那么可推得
时该命题不成立,那么可推得
A
当 时,该命题不成立
B 当
时,该命题不成立
B 当 时,该命题成立
时,该命题成立
C
当 时,该命题成立
D 当
时,该命题成立
D 当 时,该命题不成立
时,该命题不成立
5.已知对任意实数χ,有 且
且 时
时 >0,
>0, <0,则当χ<0时,
<0,则当χ<0时,
A. B.
B.
C. D.
D.
6.已知 ,在点
,在点 处连续,则实数
处连续,则实数 的值为
的值为
A.  B.
B.
 C.1
D.2
C.1
D.2
7.已知m∈R,函数 在[1,+∞)上是单调增函数,则m的最大值是
在[1,+∞)上是单调增函数,则m的最大值是
A.0 B.
8.已知 ,设在
,设在 的展开式中含
的展开式中含 项的系数为
项的系数为 ,则
,则 等于
等于
A、-2 B、 D、
D、
9.已知函数 的导函数,
的导函数,
函数 的图象如右图所示,且
的图象如右图所示,且 ,
,
则不等式 的解集为
的解集为
A. B.
B.
C.(2,3) D.
10.利用标准正态分布表我们可以求出一般正态总体在某一区间上取值的概率,若正态总体为N(1,9),则该正态分布在区间(1,10)上的概率为
A. B.
B. C.
C. D.
D.
11.下列四个命题中,不正确的是
A.若函数 在
在 处连续,则
处连续,则
B.若函数 、
、 满足
满足 ,则
,则
C.函数 =
= 的不连续点是
的不连续点是 =3和
=3和 =-3
=-3
D.
12. 设 ,函数
,函数 的导函数是
的导函数是 ,且
,且 是奇函数,若曲线
是奇函数,若曲线 的一切线斜率是
的一切线斜率是 ,则切点的横坐标为
,则切点的横坐标为
A.  B.
B.
 C.
C.
 D.
D.

二、填空题:本大题共4小题,每小题5分,共20分.把答案填在题中横线上.
13.设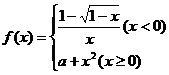 ,要使函数
,要使函数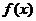 在
在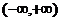 内连续,则
内连续,则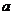 的值为
.
的值为
.
14.设等差数列{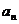 },{
},{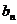 }的前
}的前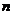 项的和分别为
项的和分别为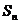 与
与 ,若
,若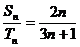 ,则
,则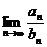 =
.
=
.
15.利用数学归纳法证明(n+1)(n+2)…(n+n)=2n?1?3?…?(2n-1)时,由k到k+1左边应添加的因式是 .
16.函数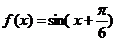 的图象按向量
的图象按向量 平移后得到
平移后得到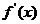 的图象,其中
的图象,其中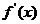 为
为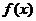 的导函数,且
的导函数,且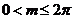 ,则
,则 .
.
三、解答题:本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤。
17.(本小题满分10分)甲、乙两篮球运动员进行定点投篮,每人各投4个球,甲投篮命中的概率为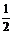 ,乙投篮命中的概率为
,乙投篮命中的概率为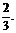
(Ⅰ)求甲至多命中2个且乙至少命中2个的概率;
(Ⅱ)若规定每投篮一次命中得3分,未命中得-1分,求乙所得分数η的概率分布和数学期望.
18.(本小题满分12分)有一个4×5×6的长方体, 它的六个面上均涂上颜色. 现将这个长方体锯成120个1×1×1的小正方体,从这些小正方体中随机地任取1个.
(Ⅰ)设小正方体涂上颜色的面数为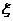 ,求
,求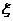 的分布列和数学期望.
的分布列和数学期望.
(Ⅱ)如每次从中任取一个小正方体,确定涂色的面数后,再放回,连续抽取6次,设恰好取到两面涂有颜色的小正方体次数为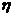 . 求
. 求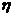 的数学期望.
的数学期望.
19.(本小题满分12分)盒内有大小相同的9个球,其中2个红色球,3个白色球,4个黑色球,规定取出1个红色球得1分,取出1个白色球得0分,取出1个黑色球得?1分.现从盒中任取3个球,(Ⅰ)求取出的3个球颜色互不相同的概率;
(Ⅱ)求取出的3个球得分之和恰为1分的概率;
(Ⅲ)设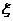 为取出的3个球中白色球的个数,求
为取出的3个球中白色球的个数,求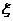 的分布列和数学期望.
的分布列和数学期望.
20.(本小题满分12分)
用长为90cm、宽为48cm的长方形铁皮做一个无盖的容器,先在四角分别截去一个小正方形,然后把四边形翻转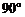 ,再焊接而成(如图),问该容器的高为多少时,容器的容积最大?
,再焊接而成(如图),问该容器的高为多少时,容器的容积最大?
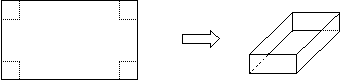 |
21.(本小题满分12分)已知函数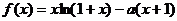 ,其中a为常数.
,其中a为常数.
(Ⅰ)若当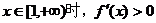 恒成立,求a的取值范围;
恒成立,求a的取值范围;
(Ⅱ)求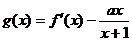 的单调区间.
的单调区间.
22.(本小题满分12分)已知函数 在点
在点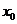 处取得极小值-4,使其导数
处取得极小值-4,使其导数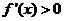 的
的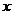 的取值范围为
的取值范围为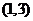 ,求:(1)
,求:(1)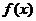 的解析式;
的解析式;
(2)若过点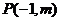 可作曲线
可作曲线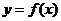 的三条切线,求实数
的三条切线,求实数 的取值范围.
的取值范围.

 郑州四中2008――2009学年高三理科数学第一次调考答题卷
郑州四中2008――2009学年高三理科数学第一次调考答题卷
一.选择题(本大题12小题,每小题5分,共60分)
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
二、填空题(本题共4小题,每小题5分,共20分.把答案填在下列横线上)
13.________________; 14.____________ ; 15. _____________; 16. _______________.
三、解答题(本题共6小题,共70分.解答题应写出文字说明、证明过程或推演步骤)
 17.解:
17.解:
 18.解:
18.解:
 19.解:
19.解:
|
 20.解:
20.解: 21.解:
21.解: 22.解:
22.解:
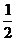 . 14.
. 14.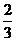 .
15.
.
15.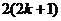 .
16.
.
16.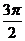 .
.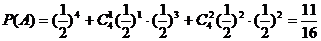 …………………………2分
…………………………2分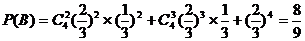 …………………………………4分
…………………………………4分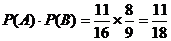 …………………………………………5分
…………………………………………5分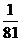
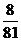
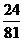
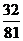
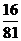
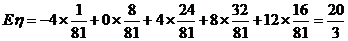 ………………………10分
………………………10分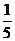
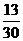
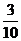
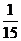
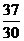
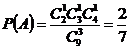 .(3分)
.(3分)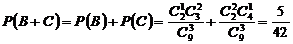 .(6分)
.(6分)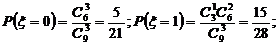
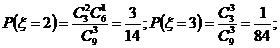

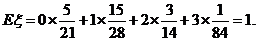 .(12分)
.(12分)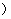 .
.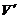 (x) = 12x2-552x + 4320
(x) = 12x2-552x + 4320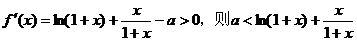 ……………2分
……………2分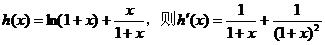
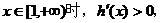 ∴
∴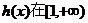 上单调递增,
上单调递增,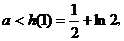 ∴a的取值范围是
∴a的取值范围是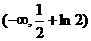 ………………………6分
………………………6分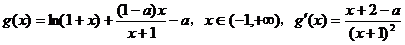
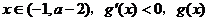 是减函数;
是减函数;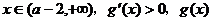 是增函数 ……………………………………8分
是增函数 ……………………………………8分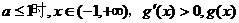 是增函数 …………………………10分
是增函数 …………………………10分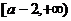 ,减区间为
,减区间为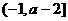 ,
,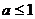 时,增区间为
时,增区间为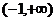 …………………………………………………12分
…………………………………………………12分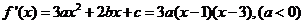
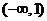 上
上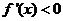 ;在
;在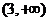 上
上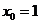 处取得极小值
处取得极小值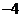
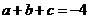 ①
①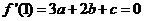 ②
②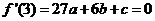 ③
③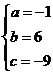
 (7分)
(7分)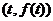
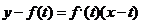
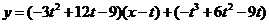

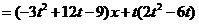 过
过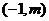
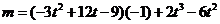
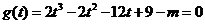
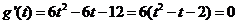 ,
,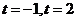 ,方程
,方程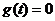 有三个根。
有三个根。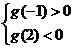
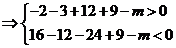
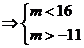
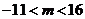
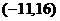 (12分)
(12分)