课题:复数的概念和运算
一、考纲要求:
1、了解数系的扩充过程,体会实际需求与数学内部的矛盾(数的运算规则、方程理论)在数系扩充过程中的作用。
2、理解复数的基本概念以及复数相等的充要条件
3、了解复数的代数表示法及其几何意义,能进行复数代数形式的四则运算,了解复数代数形式的加、减运算的几何意义。
三、基础训练:
1.复数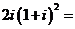 _____.
2.复数
_____.
2.复数  ______.
______.
3.复数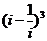 ____.4.复数
____.4.复数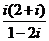 等于___.5.复数1+
等于___.5.复数1+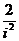 =_____.
=_____.
6.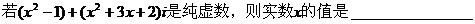 .
.
7.若复数z满足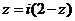 (i是虚数单位),则z=
.
(i是虚数单位),则z=
.
8.已知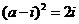 ,其中
,其中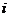 是虚数单位,那么实数
是虚数单位,那么实数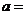 .
.
9. 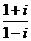 表示为
表示为
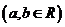 ,则
,则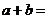 .10.复数
.10.复数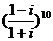 的值________.
的值________.
11. .
.

四、典型例题:

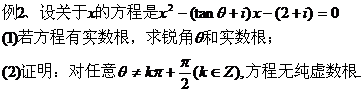
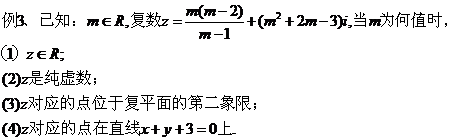
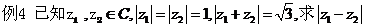

(2)已知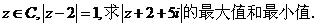
五、作业反馈:
1.设 ,且
,且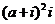 为正实数,则
为正实数,则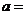 ____________.
____________.
2.设z的共轭复数是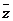 ,或z+
,或z+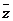 =4,z?
=4,z?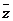 =8,则
=8,则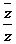 等于________.
等于________.
3.已知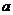 是实数,
是实数, 是纯虚数,则
是纯虚数,则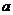 =____________.
=____________.
4.复数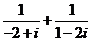 的虚部是_____________.
的虚部是_____________.
5.已知复数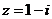 ,则
,则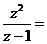 ______________.
______________.
6若复数z满足z(1+2z)=5, 则复数z的实部与虚部之差等于____________.
7、若复数z满足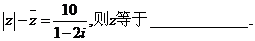
8、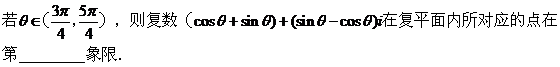
9、定义运算
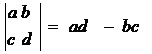 ,若复数
,若复数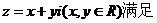
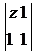 的模等于1,则复数z 对应的点Z(x,y)轨迹方程为__________.
的模等于1,则复数z 对应的点Z(x,y)轨迹方程为__________.