西安中学
师大附中
高2009届第二次模拟考试
高新一中
长安一中
数学试题(文科)
命题人:西安中学 薛党鹏
审题人:长安一中 岳建良
本试卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分.共150分,考试时间120分钟.
第I卷 (选择题,共60分)
一.选择题:本大题共12小题 每小题5分,共60分
每小题5分,共60分 在每小题给出的四个选项中,只有一项是符合题目要求的
在每小题给出的四个选项中,只有一项是符合题目要求的
1.已知集合M={x|x<3},N={x|log2x>1},则M∩N=
A.  B.{x|0<x<3} C.{x|1<x<3} D.{x|2<x<3}
B.{x|0<x<3} C.{x|1<x<3} D.{x|2<x<3}
2. 函数y=8sin4xcos4x的最小正周期是( ).
A.2π B.4π C. D.
3. 已知等差数列 中,
中, ,则前10项的和
,则前10项的和 =
=
A.100 B.210 C.380 D.400
4. 下列函数中,在其定义域内既是奇函数又是减函数的是
A. B.
B. 
C.  D.
D. 
5.某地区有300家商店,其中大型商店有30家 ,中型商店有75家,小型商店有195家.为了掌握各商店的营业情况,要从中抽取一个容量为20的样本.若采用分层抽样的方法,抽取的中型商店数是
A.2 B
6. 已知 是两条不同直线,
是两条不同直线, 是三个不同平面,下列命题中正确的是
是三个不同平面,下列命题中正确的是
A. B.
B.
C. D.
D.
7. 若双曲线 的离心率为2, 则双曲线
的离心率为2, 则双曲线 的离心率为
的离心率为
A. B.
B. C.2
D.
C.2
D.
8. 不等式 的解集是
的解集是
A. B.
B. C.
C. D.
D.
9.设 为
为 所在平面内一点,且
所在平面内一点,且 ,则
,则 的面积与
的面积与 的面积之比为
的面积之比为
A. B.
B. C.
C. D.
D.
10. 从圆 外一点
外一点 向这个圆作两条切线,则两切线夹角的余弦值为
向这个圆作两条切线,则两切线夹角的余弦值为
A. B.
B. C.
C. D.
D.
11. 若曲线 的一条切线
的一条切线 与直线
与直线 垂直,则直线
垂直,则直线 的方程为
的方程为
A. B.
B.
C. D.
D.
12. 数列 中,
中, ,
,  , 则该数列的前100项之和
, 则该数列的前100项之和 =
=
A.5 B.
第II卷(共90分)
二、填空题:本大题共4小题,每小题4分,共16分 把答案填在题中横线上
把答案填在题中横线上
13. 已知正数 、
、 满足
满足 ,则
,则 的最大值为_______.
的最大值为_______.
14.正四棱锥侧面与底面所成的角为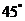 ,则其侧棱与底面所成角的正切值为 .
,则其侧棱与底面所成角的正切值为 .
15. 二项式 的展开式中的常数项为________.(结果用数值作答)
的展开式中的常数项为________.(结果用数值作答)
16. 如果一个函数的图象关于直线 对称,则称此函数为自反函数. 使得函数
对称,则称此函数为自反函数. 使得函数 为自反函数的一组实数
为自反函数的一组实数 的取值为________
的取值为________
三、解答题:本大题共6小题,共74分 解答应写出文字说明,证明过程或演算步骤
解答应写出文字说明,证明过程或演算步骤
17.(本题满分12分)已知函数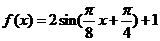 .
.
(Ⅰ)在所给的坐标纸上作出函数 的图象(不要求写出作图过程).
的图象(不要求写出作图过程).
(Ⅱ)令 ,
, .求函数
.求函数 的最小值以及取得最小值时所对应的
的最小值以及取得最小值时所对应的 的集合.
的集合.
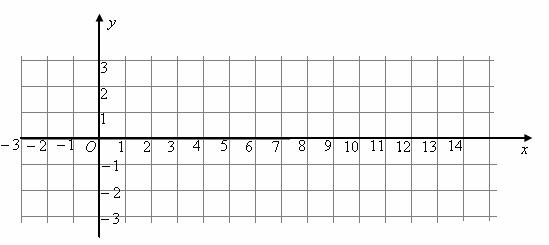
18.(本题满分12分)按照新课程的要求, 高中学生在每学期都要至少参加一次社会实践活动(以下简称活动). 该校高三一班50名学生在上学期参加活动的次数统计如图所示.
 (I)求该班学生参加活动的人均次数
(I)求该班学生参加活动的人均次数 ;
;
(II)从该班中任意选两名学生,求他们参加活动次数恰好相等的概率 .
.
(要求:答案用最简分数表示)
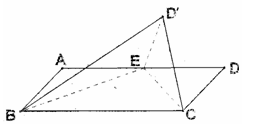 19.(本题满分12分)如图所示,在矩形
19.(本题满分12分)如图所示,在矩形 中,
中, ,点
,点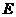 是
是 的中点,将
的中点,将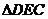 沿
沿 折起到
折起到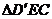 的位置,使二面角
的位置,使二面角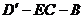 是直二面角.
是直二面角.
(1)证明: ;
;
(2)求二面角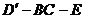 的正切值.
的正切值.
20. (本题满分12分)设函数
(I)求函数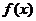 的单调区间;
的单调区间;
(II)若对任意的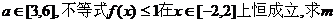 的取值范围.
的取值范围.
 21. (本题满分12分) 已知椭圆Γ的中心在原点,焦点在x轴上,它的一个顶点B的坐标为
21. (本题满分12分) 已知椭圆Γ的中心在原点,焦点在x轴上,它的一个顶点B的坐标为 ,离心率等于
,离心率等于 .直线
.直线 与椭圆Γ交于
与椭圆Γ交于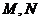 两点.
两点.
(Ⅰ)求椭圆Γ的方程;
(Ⅱ) 若椭圆Γ的右焦点 恰好为
恰好为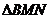 的垂心,试求出直线
的垂心,试求出直线 的方程.
的方程.
22. (本题满分14分)已知正项数列 满足对一切
满足对一切 ,有
,有 ,其中
,其中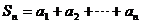 。
。
(Ⅰ)求证: 对一切 ,有
,有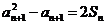 ;
;
(Ⅱ)求数列 的通项公式;
的通项公式;
(Ⅲ)求证:当 时,有
时,有 .
.
西安中学
师大附中
高2009届第二次模拟考试
高新一中
长安一中
数学答题纸(文科)
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
二、填空题:(本大题共4小题,每小题4分,共16分)
13. , 14. . 15. . 16. .
三、解答题:(本大题共6小题,共74分)
17.(Ⅰ)

(Ⅱ)
18. (Ⅰ)
(Ⅱ)
19. (Ⅰ)

(Ⅱ)
20. (Ⅰ)
(Ⅱ)
21. (I)
(II)
22. (Ⅰ)
(Ⅱ)
(Ⅲ)

西安中学
师大附中
高2009届第二次模拟考试
高新一中
长安一中
数学(文)答题纸
本试卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分.共150分,考试时间120分钟.
|

 ; 15.15; 16.
; 15.15; 16. ,
, 可以填写任一实数.
可以填写任一实数.








 6分
6分

 ,即
,即 时,函数
时,函数 取得最小值
取得最小值 .
12分
.
12分 =
= . 6分
. 6分 .
12分
.
12分 面D′EC,∴BE⊥CD′.
6分
面D′EC,∴BE⊥CD′.
6分 ∴D′M⊥平面EBC,
∴D′M⊥平面EBC,
 ,
,
 ;平面D′BC的法向量为
;平面D′BC的法向量为






 ,
,
 由(I)知
由(I)知


 ,则由题意知b = 1.
,则由题意知b = 1.
 …………………………………………………6分
…………………………………………………6分 的斜率为
的斜率为 ,从而直线
,从而直线 ,代如椭圆的方程,并整理可得
,代如椭圆的方程,并整理可得 .设
.设 ,则
,则 ,
, .于是
.于是

 或
或 .
. 即为直线
即为直线 时, 点
时, 点 是
是 的垂心. 12分
的垂心. 12分 有
有


 (
( ) 5分
) 5分 及
及



 . 10分
. 10分 ,
,
 14分
14分