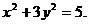2009最有影响力高考复习题(数学)10(3+3+4)
文博浪花工作室王培博推荐(
一、选择题:
1、设随机变量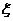 服从正态分布
服从正态分布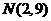 ,若
,若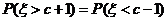 ,则
,则 = ( )
= ( )
A.1
B
?A.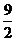 B.5
C.6
D.
B.5
C.6
D.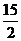 ?
?
3、已知数列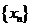 满足
满足 ,
,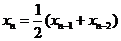 ,
,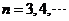 ,若
,若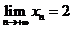 ,则
,则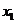 =( )
=( )
A、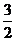 B
B 3 C、4
D、5
3 C、4
D、5
二、填空题:
4、三角形ABC中AP为BC边上的中线,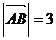 ,
,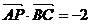 ,则
,则 =
=
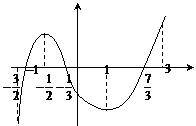 5、O为坐标原点,正△OAB中A、B在抛物线
5、O为坐标原点,正△OAB中A、B在抛物线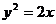 上,正△OCD中C、D在抛物线
上,正△OCD中C、D在抛物线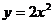 上,则△ OAB与△OCD的面积之比为
.
上,则△ OAB与△OCD的面积之比为
.
6、已知函数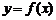 在定义域
在定义域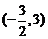 上可导,其图像如图,记
上可导,其图像如图,记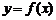 的导函数
的导函数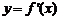 ,则不等式
,则不等式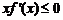 的解集是________.
的解集是________.
三、解答题:
7、同时抛掷15枚均匀的硬币一次.(1)试求至多有1枚正面向上的概率;
(2)试问出现正面向上为奇数枚的概率与出现正面向上为偶数枚的概率是否相等?请说明理由.
8、已知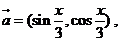
 ,函数
,函数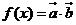 .
.
(1)将f(x)写成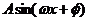 的形式,并求其图象对称中心的坐标;
的形式,并求其图象对称中心的坐标;
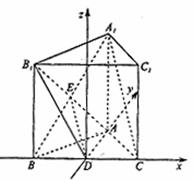
(2)如果△ABC的三边a,b,c满足b2=ac,且边b所对的角为x,试求x的范围及此时函数f(x)的值域.
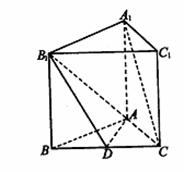
9、如图,正三棱柱ABC―A1B1C1中,D是BC的中点,AA1=AB=1.
10、设直线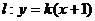 与椭圆
与椭圆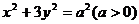 相交于A、B两个不同的点,与x轴相交于点C,记O为坐标原点.
相交于A、B两个不同的点,与x轴相交于点C,记O为坐标原点.
(I)证明: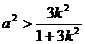
(II)若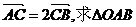 的面积取得最大值时的椭圆方程.
的面积取得最大值时的椭圆方程.
四、10答案:1、【解析】

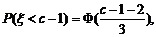
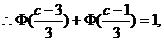
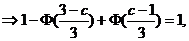 解得
解得 =2, 所以选B.
=2, 所以选B.
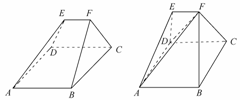
∵VF―ADE=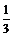 ?EF?S△ADE=
?EF?S△ADE= ×3×2=
×3×2=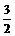 .?
.?
VF―ABCD=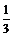 ?DE?S□ABCD=
?DE?S□ABCD=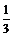 ?2?32=6.?∴V多面体=
?2?32=6.?∴V多面体=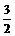 +6=
+6=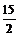 .选D.?
.选D.?
3、【解析】由条件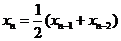 有
有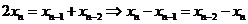 ,∴
,∴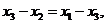
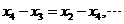

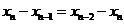 ,累加得
,累加得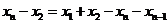 ,代入
,代入 得
得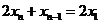 ,两边同取极限得,
,两边同取极限得,
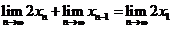 ,即
,即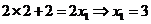 ,选B
,选B
4、【解析】 ,即
,即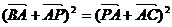 ,
,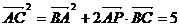 ,
,
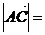
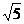 ,故选C.
,故选C.
5、【解析】设△OAB的边长为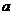 ,则不妨设
,则不妨设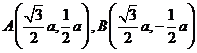 ,代入
,代入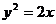 ,得
,得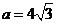 ;同理,设△OCD的边长为
;同理,设△OCD的边长为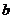 ,可得
,可得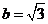 .
.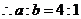 ,
,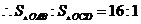 .
.
6、【解析】:本题是一道改编题,利用函数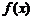 的图像信息得出
的图像信息得出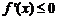 的解集是
的解集是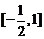 ,
,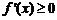 的解集是
的解集是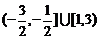 ,从而由
,从而由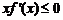 ,得
,得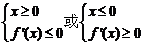 ,从而
,从而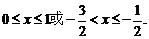
答案: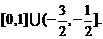
7、【解析】(1):记“抛掷1枚硬币1次出现正面向上”为事件A,P(A)=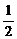
抛掷15枚均匀的硬币一次相当于做15次独立的重复试验,
根据n次独立重复试验中事件A发生k次的概率公式,记至多有1枚正面向上的概率为P1,则P1=P(0)+P(1)=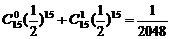
(2):记正面向上为奇数枚的概率为P2,记正面向上为偶数枚的概率为P3,则有
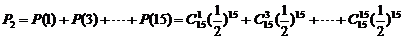

又“出现正面向上为奇数枚”的事件与“出现正面向上为偶数枚”的事件是对立事件
∴P3=1-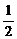 =
=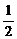 .∴出现正面向上为奇数枚的概率与出现正面向上为偶数枚的概率相等.
.∴出现正面向上为奇数枚的概率与出现正面向上为偶数枚的概率相等.
8、【解析】(1)
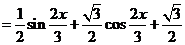
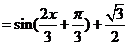 .
.
令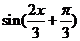 =0,得
=0,得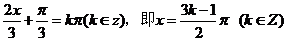 .而y=
.而y=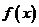 的图象可由
的图象可由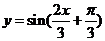 向上平移
向上平移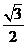 个单位得到,故所求对称中心的坐标为
个单位得到,故所求对称中心的坐标为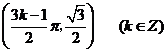 .
.
(2)由已知b2=ac,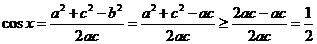

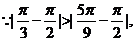
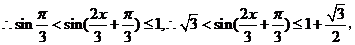
9、【解析】解法一(I)证明:连接A1B,设A1B∩AB1 = E,连接DE.
∵ABC―A1B1C1是正三棱柱,且AA1 = AB,∴四边形A1ABB1是正方形,
∴E是A1B的中点,又D是BC的中点,∴DE∥A1C.
∵DE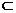 平面AB1D,A1C
平面AB1D,A1C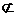 平面AB1D,∴A1C∥平面AB1D.
平面AB1D,∴A1C∥平面AB1D.
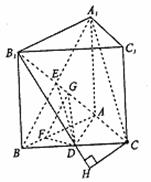
(II)解:在面ABC内作DF⊥AB于点F,在面A1ABB1内作FG⊥AB1于点G,连接DG.∵平面A1ABB1⊥平面ABC, ∴DF⊥平面A1ABB1,
∴FG是DG在平面A1ABB1上的射影, ∵FG⊥AB1, ∴DG⊥AB1
∴∠FGD是二面角B―AB1―D的平面角
设A1A
= AB = 1,在正△ABC中,DF=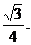
在△ABE中,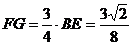 ,在Rt△DFG中,
,在Rt△DFG中,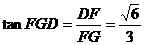 ,
,
所以,二面角B―AB1―D的大小为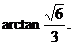
(III)解:∵平面B1BCC1⊥平面ABC,且AD⊥BC,
∴AD⊥平面B1BCC1,又AD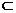 平面AB1D,∴平面B1BCC1⊥平面AB1D.
平面AB1D,∴平面B1BCC1⊥平面AB1D.
在平面B1BCC1内作CH⊥B1D交B1D的延长线于点H,则CH的长度就是点C到平面AB1D的距离.
由△CDH∽△B1DB,得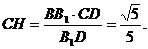 即点C到平面AB1D的距离是
即点C到平面AB1D的距离是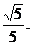
解法二:建立空间直角坐标系D―xyz,如图,(I)证明:连接A1B,设A1B∩AB1 = E,连接DE.
设A1A = AB = 1,
则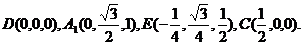
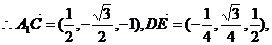
|

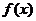 的值域为
的值域为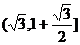 .综上所述,
.综上所述,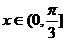 ,
,
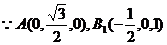 ,
, 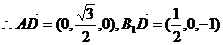 ,
, 是平面AB1D的法向量,则
是平面AB1D的法向量,则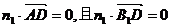 ,
,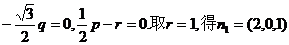 ;同理,可求得平面AB1B的法向量是
;同理,可求得平面AB1B的法向量是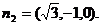
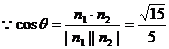 ,∴二面角B―AB1―D为
,∴二面角B―AB1―D为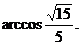
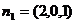 ,
,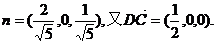 ∴点C到平面AB1D的距离
∴点C到平面AB1D的距离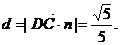
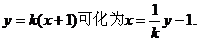
 ,得
,得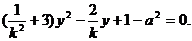 ①
①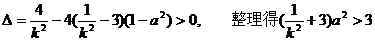 ,即
,即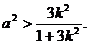
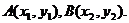 由①,得
由①,得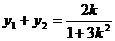
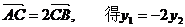 ,代入上式,得
,代入上式,得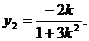
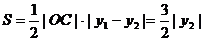
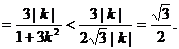
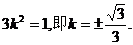 由
由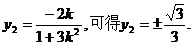
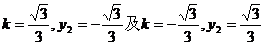 这两组值分别代入①,均可解出
这两组值分别代入①,均可解出