湖南省长沙市一中2009年高三第二次模拟试卷
文科数学
命题:长沙市一中高三文科备课组
时量:120分钟 满分:150分
一、选择题(第小题5分,共8小题,共40分,每小题只有一个选项是正确的)
1.化简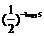 的值为( )
的值为( )
A.?5 B.? C.5 D.
C.5 D.
2.为得到函数y = log22x的图象,可以把函数y = log2x的图象( )
A.向上平移一个单位 B.向下平移一个单位
C.向左平移一个单位 D.向右平移一个单位
3.函数y = cos (x + 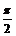 )的一个单调递增区间是( )
)的一个单调递增区间是( )
A.[?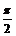 ,
,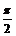 ] B.[
] B.[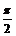 ,
,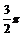 ] C.[?
] C.[? ,0] D.[0,
,0] D.[0, ]
]
4.若平面向量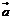 与向量
与向量 = (1,?2)的夹角为180°,且|
= (1,?2)的夹角为180°,且|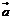 | =
| = 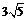 ,则
,则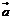 = ( )
= ( )
A.(?3,6) B.(3,?6) C.(6,?3) D.(?6,3)
5.甲、乙、丙、丁四位同学计划暑假分别外出旅游,有A、B、C三条线路可选,若每条线路至少有1人选择,则不同的安排方法有( )
A.72种 B.36种 C.18种 D.16种
6.与圆x2 + (y + 5)2 = 3相切,且纵截距和横截距相等的直线共有( )
A.2条 B.3条 C.4条 D.6条
7.等差数列{an}各项为正数,公差为2,前n项和为Sn,若 {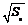 }也是等差数列,则a1 = ( )
}也是等差数列,则a1 = ( )
A.1 B.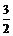
8.已知平面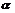 ∥
∥ ,直线l
,直线l
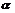 ,点P∈l,平面
,点P∈l,平面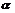 、
、 间的距离为5,则在
间的距离为5,则在 内到点P的距离为13且到直线l的距离为
内到点P的距离为13且到直线l的距离为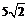 的点的轨迹是( )
的点的轨迹是( )
A.一个圆 B.双曲线的一支 C.两条直线 D.四个点
 二、填空题(每小题5分,共7小题,共35分)
二、填空题(每小题5分,共7小题,共35分)
9.若sin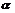 =
=  ,则cos2
,则cos2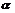 = .
= .
10.( )6的展开式中的常数项为 .
)6的展开式中的常数项为 .
11.统计某校1000名学生的数学会考成绩,得到样本频率分布直方图,规定不低于60分为及格,不低于80分为优秀,则及格人数为 ;优秀率为 .
12.集合A = {y| y = x2
+ 2x ? 3},B = {y| y = x +  ,x<0},则A∩B = .
,x<0},则A∩B = .
13.正三棱锥P ― ABC底面正三角形的边长为1,其外接球球心O为△ ABC的重心,则此正三棱锥的体积为 .
14.某公司一年购买某种货物400吨,每次都购买x吨,运费为4万元/次,一年的总存储费用为4x万元,要使一年的总运费和总存储费用之和最小,则x = 吨.
15.我们把在线段上到两端点距离之比为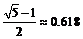 的点称为黄金分割点。类似地,在解析几何中,我们称离心率为
的点称为黄金分割点。类似地,在解析几何中,我们称离心率为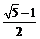 的椭圆为黄金椭圆,已知
的椭圆为黄金椭圆,已知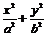 = 1 (a>b>0)是黄金椭圆,给出下列四个命题:
= 1 (a>b>0)是黄金椭圆,给出下列四个命题:
①a、b、c成等比数列;
②若F2为右焦点,B为上顶点,A1为左顶点,则:
③以两通径的4个端点为顶点的四边形为正方形;
④若直线l过椭圆中心,与椭圆交于点E、F,P为椭圆上任意一点(除顶点外),则KPE? KPF为定值.
其中正确命题的序号为 .
三、解答题
16.(本小题满分12分)一项“过关游戏”规定:在第n关要抛掷一颗均匀的骰子n次,如果第n关的n次抛掷所出现的点数之和大于n2就算过关.问:
(1)玩家小强在这项游戏中最多能连过几关?
(2)他连过前两关的概率是多少?
17.(本小题满分12分)设函数f (x)
= 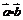 ,其中向量
,其中向量 =
= 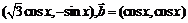 .
.
①若函数y = sin2x按向量 = (p,q) (|p|<
= (p,q) (|p|<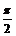 )平移后得到函数y = f (x)的图象,求实数p,q的值.
)平移后得到函数y = f (x)的图象,求实数p,q的值.
②若f (x) = 1 + 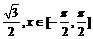 ,求sinx.
,求sinx.
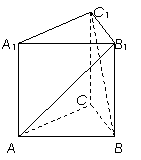 18.(本小题满分12分)如图:正三棱柱ABC―A1B1C1中,底面边长为2,侧棱长为
18.(本小题满分12分)如图:正三棱柱ABC―A1B1C1中,底面边长为2,侧棱长为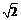 ,若经过对角线AB1且与对角线BC1平行的平面交上底面于DB1.
,若经过对角线AB1且与对角线BC1平行的平面交上底面于DB1.
(1)试确定D点的位置,并证明你的结论;
(2)求二面角A1―AB1―D的大小.
19.(本小题满分13分)数列{an}前n项和为Sn,Sn = 2an ? 3n (n∈N*)
(1)若数列{an + t}成等比数列,求常数t 的值;
(2)求数列{an}的通项公式;
(3)数列{an}中是否存在三项,它们可以构成等差数列?若存在,请求出一组适合条件的项;若不存在,请说明理由.
20.(本小题满分13分)已知x=1是函数 的一个极值点,
的一个极值点, 且m<0
且m<0
(1)求m与n的关系表达式;
(2)若f (x)的单调区间;
(3)当 时,函数y= f (x)的的图象上任意一点的切线斜率恒大于3m,求m的取值范围.
时,函数y= f (x)的的图象上任意一点的切线斜率恒大于3m,求m的取值范围.
21.(本小题满分13分)已知函数y = kx与y = x2 + 2 (x≥0)的图象相交于不同两点A (x1,y1),B (x2,y2),l1,l2分别是y = x2 + 2 (x≥0)的图象在A、B两点的切线,M、N分别是l1、l2与x轴的交点,P为l1与l2的交点.
(1)求证:直线l1,y = kx,l2的斜率成等差数列;
(2)求l1与l2交点P的轨迹方程;
(3)是否存在实数k使得△ABP的面积最大?若存在,请求出k的值;若不存在,请说明理由.
第二次模拟考试文科数学教师用卷
一、选择题(第小题5分,共8小题,共40分,每小题只有一个选项是正确的)
1.化简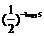 的值为( C )
的值为( C )
A.?5 B.? C.5 D.
C.5 D.
2.为得到函数y = log22x的图象,可以把函数y = log2x的图象( A )
A.向上平移一个单位 B.向下平移一个单位
C.向左平移一个单位 D.向右平移一个单位
3.函数y = cos (x + 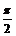 )的一个单调递增区间是( B )
)的一个单调递增区间是( B )
A.[?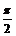 ,
,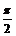 ] B.[
] B.[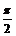 ,
,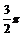 ] C.[?
] C.[? ,0] D.[0,
,0] D.[0, ]
]
4.若平面向量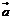 与向量
与向量 = (1,?2)的夹角为180°,且|
= (1,?2)的夹角为180°,且|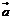 | =
| = 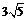 ,则
,则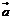 = ( A )
= ( A )
A.(?3,6) B.(3,?6) C.(6,?3) D.(?6,3)
5.甲、乙、丙、丁四位同学计划暑假分别外出旅游,有A、B、C三条线路可选,若每条线路至少有1人选择,则不同的安排方法有( B )
A.72种 B.36种 C.18种 D.16种
6.与圆x2 + (y + 5)2 = 3相切,且纵截距和横截距相等的直线共有( C )
A.2条 B.3条 C.4条 D.6条
7.等差数列{an}各项为正数,公差为2,前n项和为Sn,若 {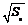 }也是等差数列,则a1 = ( A )
}也是等差数列,则a1 = ( A )
A.1 B.2 C.3 D.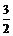
8.已知平面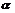 ∥
∥ ,直线l
,直线l
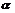 ,点P∈l,平面
,点P∈l,平面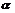 、
、 间的距离为5,则在
间的距离为5,则在 内到点P的距离为13且到直线l的距离为
内到点P的距离为13且到直线l的距离为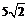 的点的轨迹是( D )
的点的轨迹是( D )
A.一个圆 B.双曲线的一支 C.两条直线 D.四个点
 二、填空题(每小题5分,共7小题,共35分)
二、填空题(每小题5分,共7小题,共35分)
9.若sin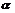 =
=  ,则cos2
,则cos2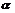 =
= 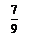 .
.
10.( )6的展开式中的常数项为 15 .
)6的展开式中的常数项为 15 .
11.统计某校1000名学生的数学会考成绩,得到样本频率分布直方图,规定不低于60分为及格,不低于80分为优秀,则及格人数为 800 ;优秀率为 20% .
12.集合A = {y| y = x2
+ 2x ? 3},B = {y| y = x +  ,x<0},则A∩B = [?4,?2] .
,x<0},则A∩B = [?4,?2] .
13.正三棱锥P ― ABC底面正三角形的边长为1,其外接球球心O为△ ABC的重心,则此正三棱锥的体积为 .
.
14.某公司一年购买某种货物400吨,每次都购买x吨,运费为4万元/次,一年的总存储费用为4x万元,要使一年的总运费和总存储费用之和最小,则x = 20 吨.
15.我们把在线段上到两端点距离之比为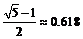 的点称为黄金分割点。类似地,在解析几何中,我们称离心率为
的点称为黄金分割点。类似地,在解析几何中,我们称离心率为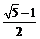 的椭圆为黄金椭圆,已知
的椭圆为黄金椭圆,已知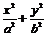 = 1 (a>b>0)是黄金椭圆,给出下列四个命题:
= 1 (a>b>0)是黄金椭圆,给出下列四个命题:
①a、b、c成等比数列;
②若F2为右焦点,B为上顶点,A1为左顶点,则:
③以两通径的4个端点为顶点的四边形为正方形;
④若直线l过椭圆中心,与椭圆交于点E、F,P为椭圆上任意一点(除顶点外),则KPE? KPF为定值.
其中正确命题的序号为 ①②③④ .
三、解答题
16.(本小题满分12分)一项“过关游戏”规定:在第n关要抛掷一颗均匀的骰子n次,如果第n关的n次抛掷所出现的点数之和大于n2就算过关.问:
(1)玩家小强在这项游戏中最多能连过几关?
(2)他连过前两关的概率是多少?
【解析】(1)因为点数最大为6,抛掷n次点数之和的最大值为6n,所以6×1>12,6×2>22,6×3>32,6×4>42,6×5>52,6×6 = 62,6×7<72,……,当n≥6时,点数之和不可能大于n2,即此时过关的概率为0.所以小强在这项游戏中最多能连过5关.
(2)记第n次过关为事伯An,基本事件总数为6n.
第一关:由12 = 1知,点数不小于2即可,所以P (A1)
=  ,
,
第二关:由22 = 4知,考虑对立事件 ,即“不能过第二关”依次取a = 2,3,4,解不定方程x + y
= a,得其解的个数是
,即“不能过第二关”依次取a = 2,3,4,解不定方程x + y
= a,得其解的个数是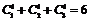 ,从而P (A2) = 1 ? P
,从而P (A2) = 1 ? P .所以他连过前两关的概率是P =
.所以他连过前两关的概率是P = 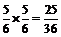 . (12分)
. (12分)
17.(本小题满分12分)设函数f (x)
= 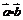 ,其中向量
,其中向量 =
= 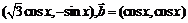 .
.
①若函数y = sin2x按向量 = (p,q) (|p|<
= (p,q) (|p|<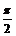 )平移后得到函数y = f (x)的图象,求实数p,q的值.
)平移后得到函数y = f (x)的图象,求实数p,q的值.
②若f (x) = 1 + 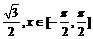 ,求sinx.
,求sinx.
【解析】①f (x) =  cos2x ? sinx cosx =
cos2x ? sinx cosx = 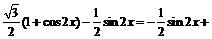
 = sin
= sin 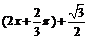 ∴
∴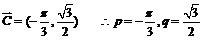 (6分)
(6分)
②sin (2x + 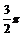 ) +
) +  ∴sin (2x +
∴sin (2x + 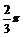 ) = 1 ∴2x +
) = 1 ∴2x + 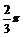 =
= 
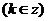
∴2x = 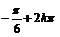 x
=
x
=  (k∈Z) ∵x∈[
(k∈Z) ∵x∈[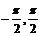 ],∴x =
],∴x = 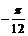 (10分)
(10分)
∴sin (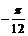 ) =
) =  (12分)
(12分)
 18.(本小题满分12分)如图:正三棱柱ABC―A1B1C1中,底面边长为2,侧棱长为
18.(本小题满分12分)如图:正三棱柱ABC―A1B1C1中,底面边长为2,侧棱长为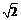 ,若经过对角线AB1且与对角线BC1平行的平面交上底面于DB1.
,若经过对角线AB1且与对角线BC1平行的平面交上底面于DB1.
(1)试确定D点的位置,并证明你的结论;
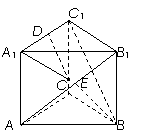 (2)求二面角A1―AB1―D的大小.
(2)求二面角A1―AB1―D的大小.
【解析】(1)点D为A1C1中点。证明如下 (2分)
设AB1与A1B交于点E,连结DE,∴DE∥BC1 ∴BC1∥面DAB1
∴面DAB1即为所求平面,D点即为所求 (6分)
|
 ∴
∴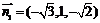
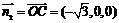 ,设
,设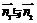 的夹角为
的夹角为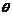 ,则cos
,则cos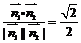 ,又知二面角A1―AB1―D是锐角,所以二面角A1―AB1―D的大小为
,又知二面角A1―AB1―D是锐角,所以二面角A1―AB1―D的大小为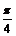 12分
12分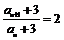 ∴t = 3
(5分)
∴t = 3
(5分)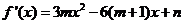 在x=1处的值为0,
在x=1处的值为0,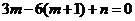 ∴
∴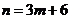
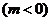 ……3分
……3分 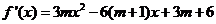 ,
,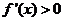 ,∴
,∴
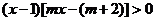
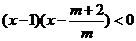
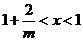 ,
,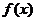 的增区间为
的增区间为 ,减区间为
,减区间为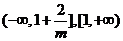 …… 6分
…… 6分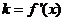
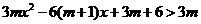
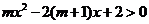
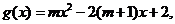 此抛物线顶点横坐标为
此抛物线顶点横坐标为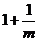
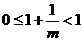 时,即
时,即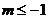 时,
时,
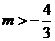 ∴
∴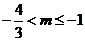 ……9分
……9分
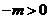 ,即
,即 ∴
∴ ……12分
……12分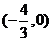 ……13分
……13分 即l1,l2的斜率分别为2x1,2x2.又由
即l1,l2的斜率分别为2x1,2x2.又由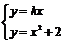 得x2 ? kx + 2 = 0 ①
得x2 ? kx + 2 = 0 ①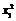 + 2),B (x2,
+ 2),B (x2,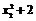 ),∴l1,l2的方程分别为:
),∴l1,l2的方程分别为: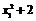
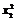 ? 2 = 2x2 (x ? x2) ,
即:y = 2x2 x ?
? 2 = 2x2 (x ? x2) ,
即:y = 2x2 x ?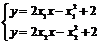 ②
② 
 ,
,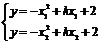
 ) + k
(x1 + x2) +4 = ?(x1
+ x2)2 + 2x1x2 + k (x1 + x2) + 4
) + k
(x1 + x2) +4 = ?(x1
+ x2)2 + 2x1x2 + k (x1 + x2) + 4 = k2 ? 8>0且x =
= k2 ? 8>0且x = 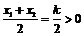 ,
,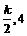 )到直线y = kx的距离d =
)到直线y = kx的距离d = 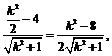
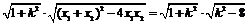 ,
,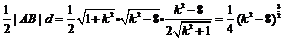 ,
,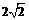 ,∴S△ABP无最大值.
,∴S△ABP无最大值.