2009-2010学年度潍坊市奎文区初中学段第一学期九年级期中考试
数学试卷
时间:90分钟 满分:120分
一、选择题(本题共12小题,共36分,在每小题给出的四个选项中,只有一个是正确的,请把正确的选项选出来.每小题选对得3分,选错、不选或选出的答案超过一个均记零分.)。
1.下列方程中,是关于 的一元二次方程的是( ) .
的一元二次方程的是( ) .
A.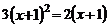
 B.
B.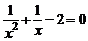
C. D.
D.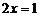
2.在比例尺为1:5000的地图上,量得甲,乙两地的距离25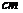 ,则甲,乙两地的实际距离是( ).
,则甲,乙两地的实际距离是( ).
A.1250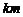 B.
B.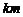 C.12.5
C.12.5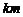 D.1.25
D.1.25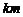
3.如图,在Rt△ABC中,∠ACB=90°,BC=1,AB=2,则下列结论正确的是( ) .
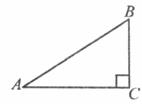
A.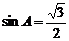 B.
B. C.
C.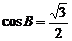 D.
D.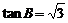
4.用位似图形的方法,可以将一个图形放大或缩小,位似中心的位置可以选在( ).
A.原图形的外部 B.原图形的内部 C.原图形的边上 D.任意位置
5.如图,厨房角柜的台面是三角形,如果把各边中点的连线所围成的三角形铺成黑色大理石(图中阴影部分)。其余部分铺成白色大理石,那么黑色大理石的面积与白色大理石面积的比是( ).
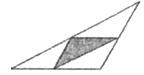
A.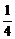 B.
B.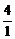 C.
C.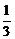 D.
D.
6.用配方法解方程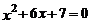 ,下面配方正确的是( ).
,下面配方正确的是( ).
A.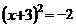 B.
B.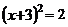 C.
C. D.
D.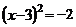
7.关于 的一元二次方程
的一元二次方程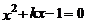 的根的情况是( ).
的根的情况是( ).
A.有两个不相等的同号实数根 B.有两个不相等的异号实数根
C.有两个相等的实数根 D.没有实数根
8.如图,小正方形的边长均为1,则下列图中的三角形(阴影部分)与△ABC相似的是( ).

9.关于 的一元二次方程
的一元二次方程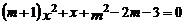 有一个根是0,则
有一个根是0,则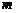 的值为( ).
的值为( ).
A.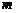 =3或
=3或 B.
B.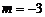 或
或 C.
C. D.
D.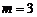
10.已知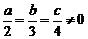 ,则
,则 的值为( ).
的值为( ).
A.
 B.
B.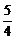 C.2 D.
C.2 D.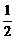
11.如图,在△ABC中,AB=12,AC=10,BC=9,AD是BC边上的高.将△ABC按如图所示的方式折叠,使点A与点D重合,折痕为EF,则△DEF的周长为( ).

A.9.5 B.10.5 C.11 D.15.5
12.如图所示,在一边靠墙(墙足够长)空地上,修建一个面积为672 的矩形临时仓库,仓库一边靠墙,另三边用总长为76
的矩形临时仓库,仓库一边靠墙,另三边用总长为76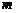 的栅栏围成,若设栅栏AB的长为
的栅栏围成,若设栅栏AB的长为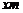 ,则下列各方程中,符合题意的是( ).
,则下列各方程中,符合题意的是( ).

A. B.
B.
C.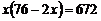 D.
D.
二、填空题(本大题共5小题,共15分.只要求填写最后结果,每小题填对得3分.)
13. =________.
=________.
14.如图,△OAB的顶点B的坐标为(4,0),把△OAB沿 轴向右平移得到△CDE,如果CB=1,那么OE的长为________.
轴向右平移得到△CDE,如果CB=1,那么OE的长为________.

15.若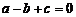 ,
,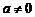 ,则方程
,则方程 必有一个根是________.
必有一个根是________.
16.如图所示,D、E两点分别在△ABC的两条边上,且DE与BC不平行,请填上一个你认为合适的条件________,使得△ADE∽△ABC.

17.如图,在平行四边形ABCD中,M、N为AB的三等分点,DM,DN分别交AC于P、Q两点,则AP:PQ:QC=________.

三、解答题(本大题共6题,共69分.解答应写出文字说明、证明过程或推演步骤.)
18.本题满分12分,每小题6分)
解下列方程
(1)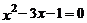
(2)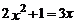 (用配方法)
(用配方法)
19.(本题满分10分)如图,在△ABC中,已知DE∥BC,AD=4,DB=8,DE=3.
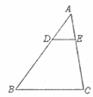
求:(1) 的值;
的值;
(2)BC的长.
20.(本题满分11分)已知,在四边形ABCD中,AD=BC,P是对角线AC的中点,M是DC的中点,N是AB的中点.
求证:∠PMN=∠PNM.

21.(本题满分12分)已知关于 的方程
的方程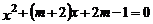 .
.
(1)求证:方程有两个不相等的实数根;
(2)当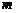 为何值时,方程的两根互为相反数?并求出此时方程的解.
为何值时,方程的两根互为相反数?并求出此时方程的解.
22.(本题满分12分)如图,网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.△ACB和△DCE的顶点都在格点上,ED的延长线交AB于点F.
(1)求证:△ACB∽△DCE;
(2)求证:EF⊥AB.

23.(本题满分12分)随着人民生活水平的不断提高,我市家庭轿车的拥有量逐年增加,据统计,某小区2006年底拥有家庭轿车64辆,2008年底家庭轿车的拥有量达到100辆.
(1)若该小区2006年底到2009年底家庭轿车拥有量的年平均增长率都相同,求该小区到2009年底家庭轿车将达到多少辆? 
(2)为了缓解停车矛盾,该小区决定投资15万元再建造若干个停车位.据测算,建造费用分别为室内车位5000元/个,露天车位1000元/个,考虑到实际因素,计划露天车位的数量不少于室内车位的2倍,但不超过室内车位的2.5倍,求该小区最多可建两种车位各多少个?试写出所有可能的方案.