2009年江苏新课标期末测试(B卷)
数学试卷
一、精心选一选.(每题3分,共30分)
1.一元二次方程 2―2
2―2 =0的解是 ( )
=0的解是 ( )
A.0 B.0或
2.下列方程没有实数根的是 ( )
A. 2一
2一 一1=0 B.
一1=0 B. 2―6
2―6 +5=0
+5=0
C. 2―2
2―2
 +3=0 D.2
+3=0 D.2 2+
2+ +1=0
+1=0
3.关于 的一元二次方程
的一元二次方程 2+(2k+1)
2+(2k+1) +k一l=0根的情况是 ( )
+k一l=0根的情况是 ( )
A.有两个不相等实数根 B.有两个相等实数根
C.没有实数根 D.根的情况无法判定
4.计算:sin20°―cos20°的值是(保留四个有效数字) ( )
A.一0.5976 B.
5.已知 、y为实数,y=
、y为实数,y= ,则y
,则y 的值等于 ( )
的值等于 ( )
A.8 B.
6.估计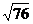 的大小应在 ( )
的大小应在 ( )
A.7~8之间 B.8.0~8.5之间 C.8.5~9.0之间 D.9~10之间
7.如图,在 ABCD中,AB:AD=3:2,∠ADB=60°,那么cosA的值等于 ( )
ABCD中,AB:AD=3:2,∠ADB=60°,那么cosA的值等于 ( )

A. B.
B.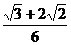 C.
C. D.
D.
8.如果线段上一点P把线段分割为两条线段PA、PB,当PA2=PB?AB,即PA≈ 0.618AB时,则称点P是线段AB的黄金分割点,现已知线段AB=10,点P是线段AB的黄金分割点,如图所示,那么线段PB的长约为 ( )

A.6.18 B.
9.如图,一个小球从A点沿制定的轨道下落,在每个交叉口都有向左或向右两种机会均等的结果,小球最终到达H点的概率是 ( )

A. B.
B. C.
C. D.
D.
10.某电视台举行歌手大奖赛,每场比赛都有编号为1~10号共10道综合素质测试题供选手随机抽取作答.在某场比赛中,前两位选手分别抽走了2号、7号题,第3位选手抽中8号题的概率是 ( )
A. B.
B. C.
C. D.
D.
二、耐心填一填.(每题2分,共20分)
11.关于 的方程(m一
的方程(m一 )
)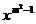 一
一 +3=0是一元二次方程,则m=________.
+3=0是一元二次方程,则m=________.
12.如果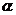 、
、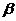 是一元二次方程
是一元二次方程 的两个根,那么
的两个根,那么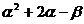 的值是______.
的值是______.
13.当 =_______时,
=_______时,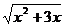 与
与 既是最简二次根式,被开方数又相同.
既是最简二次根式,被开方数又相同.
14.在比例尺为20:l的图纸上,某矩形零件面积为
15.如图,△ABC中,中线BD与CE相交于O点,S△ADE=1,则S四边形BCDE=__________.

16.小宁想知道校园内一棵大树的高度(如下图),他测得CB的长度为

17.如下图,创新广场上铺设了一种新颖的石子图案,它由五个过同一点且半径不同的圆组成,其中阴影部分铺黑色石子,其余部分铺白色石子.小鹏在规定地点随意向图案内投掷小球,每球都能落在图案内.经过多次试验,发现落在一、三、五环(阴影)内的概率分别是0.04,0.2,0.36,如果最大圆的半径是l m,那么黑色石子区域的总面积约为_______rn2.(精确到0.

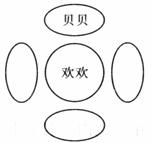
18.如下图,北京奥运的5个吉祥物“福娃”都已放置在展桌上,其中“欢欢”和“贝贝”的位置已确定,则在另外三个位置中任取两个,其中有“迎迎”的概率为___________.
19.含有4种花色的36张扑克牌的牌面都朝下,每次抽出一张记下花色后再原样放回,洗匀牌后再抽.不断重复上述过程,记录抽到红心的频率为25%,那么其中扑克牌花色是红心的大约有_________张.
20.为了测量校园水平地面上一棵不可攀的树的高度,学校数学兴趣小组做了如下的探索.根据光的反射定律,利用一面镜子和一根皮尺,设计如下图所示的测量方案:把一面很小的镜子放在离树底(B)8.

三、用心想一想.(共50分)
21.(6分)计算:

22.(每小题4分,共8分)解方程:
(1) 2―12
2―12 ―4=0 (2)
―4=0 (2)  2+2
2+2 =2
=2
23.(8分)某商场将进货价为30元的台灯以40元售出,平均每月能售出600个.调查表明:这种台灯的售价每上涨l元,其销售量就将减少l0个.为了实现平均每月l0000元的销售利润,这种台灯的售价应定为多少?这时应进台灯多少个?请你利用方程解决这一问题.
24.(8分)某校有A、B两个餐厅,甲、乙、丙三名学生各自随机选择其中的一个餐厅用餐.
(1)求甲、乙、丙三名学生在同一个餐厅用餐的概率;
(2)求甲、乙、丙三名学生中至少有一人在B餐厅用餐的概率.
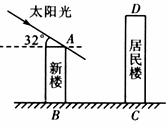
25.(10分)如下图所示,某居民小区有一朝向为正南方向的居民楼,该居民楼的一楼是高
(1)问超市以上的居民住房采光是否有影响,为什么?
(2)若要使超市采光不受影响,两楼应相距多少米?
(结果保留整数,参考数据:sin32°≈ ,cos32°≈
,cos32°≈ ,tan30°≈
,tan30°≈ )
)
26.(10分)如图所示,四边形ABCD为正方形,E是(如的中点,P在BC上,如果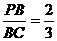 ,那么请你判断△APB和△PCE是否相似,并写出你的理由.
,那么请你判断△APB和△PCE是否相似,并写出你的理由.
