2007-2008学年度济宁汶上第二学期八年级期末质量监测
数学试卷
一、选择题。每小题3分,共36分,下列各题只有一个正确选项,
1.下列各式中,与分式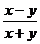 相等的是( )
相等的是( )
A. B.
B.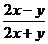 C.
C.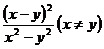 D.
D.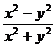
2.有四个算式:①a2÷a3=a-1=1/a;②m10÷m10=0;③(1/5)-3=1/53=1/125;④(0.01)0=1000,其中正确的算式有( )
A.3个 B.2个 C.1个 D.0个
3.如图是广告公司为某种商品设计的商标图案,若每个小正方形的面积都是1,则阴影部分的面积为( )
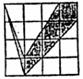
A.5 B.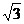 D.4
D.4
4.小明正在研究函数y=1/x的性质,下面他的几种说法中错误的是( )
A.无论x取何值,xy总是一个定值
B.在自变量取值范围内,y随着x的增大而减小
C.函数y=1/x的图象关于y=-x称
D.函数y=1/x的图象与y=x的图象有两个交点
5.如图,在等腰△ABC中,AB=AC=5,BC=6,E是BC边上的任意一点,过E作EM∥AB,交AC于M,EN∥AC,交AB于N,那么平行四边形AMEN的周长是( )
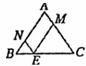
A.16 B.
6.一个矩形的面积是6,则这个矩形的一组邻边长X与Y的函数关系式的图象是( )
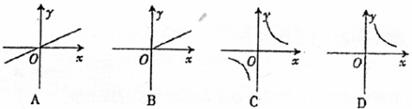
7.班主任为了解学生星期六、星期日在家的学习情况,家访了班内的六位学生,了解到他们在家的学习时间如下表所示,那么这六位学生学习时间的众数与中位数分别是( )
学生姓名
小丽
小明
小颖
小华
小乐
小恩
学习时间(小时)
4
6
3
4
5
8
A.4小时和4.5小时 B.4.5小时和4小时
C.4小时和3.5小时 D.3.5小时和4小时
8.若一组数据1,2,3,x的极差为6,则x的值是( )
A.7 B.
9.已知一组数据x1,x2,x3,如表所示,那么另一组数据2x1-1,2x2-1,2x3-1的平均数和方差分别是( )
x1
x2
x3
1
2
3
A.2,2/3 B.3,1/
10.如图,矩形AOCB的两边OC、OA分别位于x轴、y轴上,点B的坐标为B(-20/3,5),D是AB边上的点,将△ADO沿直线OD翻折,使A点恰好落在对角线OB上的点E处,若点E在一反比例函数的图像上,那么该函数的解析式是( )
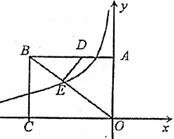
A.y=12/x B.y=6/x C.y=-6/x D.y=-12/x
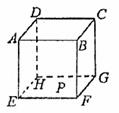
11.如图是一个棱长为
A.130 B.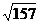 C.10
C.10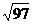 D.不确定
D.不确定
12.孔子文化节期间,几名同学包租一辆面包车前去游玩,面包车的出租价为180元,出发时又增加了两名同学,结果每位同学比原来少摊了3元车费,若设实际参加旅游的学生有x人,则下列方程正确的为( )
A.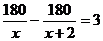 B.
B.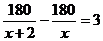
C.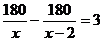 D.
D.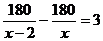
二、填空题(每小题3分,共18分)
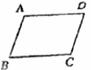
13.如图,四边形ABCD中,AB∥CD。要使四边形ABCD为平行四边形,则应添加的条件是___________。
14.已知双曲线y=k/x经过点(-1,3),如果A(a1、b1)、B(a2,b2)两点在双曲线上,且a1<a2<0,那么b1___________b2。(填“>”、“<”或“=”)
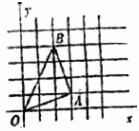
15.如图,在平面直角坐标系中点A、B的坐标分别为A(3,1),B(2,4),则△AOB是___________三角形,理由是___________。
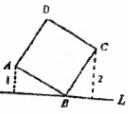
16.如图,直线L过正方形ABCD的顶点B,点A、C到直线L的距离分别是1和2,则正方形的边长是___________。
17.计算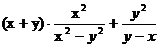 =___________.
=___________.
18.一个工人生产某种零件。计划30天完成。若每天多生产5个,则在26天完成,且多生产出15个。求这个工人原计划每天生产多少个零件?若设原计划每天生产x个零件,由题意可列方程为___________。
三、解答题。(共66分)
19.(8分)先化简再求值。
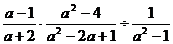 ,其中a满足a2-a=0
,其中a满足a2-a=0
20.(8分)解方程:
21.(8分)一次函数y=kx+b的图象与反比例函数y=-8/x的图象交于A、B两点,且点A的横坐标和点B的纵坐标都是-2,求这个一次函数的解析式。
22.(8分)如图,正方形网格中的每个小正方形的边长都是1,每个小格的顶点叫格点,以格点为顶点按下列要求画三角形:

(1)以格点为格点画一个三角形,使三边长分别为2、3、 :
:
(2)判断(1)中的三角形是否为直角三角形。
23.(8分)如图,沿折痕AE叠矩形ABCD的一边,使点D落在BC边上的点F处,若AB=8,且△ABF的面积为24,求EC的长。
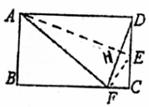
24.(8分)某一工程,在工程招标时,接到甲、乙两个工程队的投标书,施工一天需付甲工程队程款1.5万元,付乙工程队工程款1.1万元,工程领导小组根据甲、乙两队的投标书测算,可有三种施工方案:
A.甲队单独完成这项工程刚好如期完成;
B.乙队单队完成这项工程比规定日期多用5天;
C.若甲、乙两队合作4天,余下的工程由乙队单独也正好如期完成。
在不耽误工程的前提下,你觉得哪一种施工方案最节省工程款?
25.(本小题满分8分)
某高科技产品开发公司现有员工50名,所有员工的月工资情况如下表:
员工
管理人员
普通工作人员
人员结构
总经理
部门经理
科研人员
销售人员
高级技工
中级技工
勤杂工
员工数(名)
1
3
2
3
?
24
1
每人月工资(元)
21000
8400
2025
2200
1800
1600
950
请你根据上述内容。解答下列问题:
(1)该公司“高级技工”有___________名;
(2)所有员工月工资的平均数x为2500元,中位数是_______元,众数为____________。
(3)小张到这家公司应聘普通工作人员。
请你回答图中小张的问题,并指出用(2)中的哪个数据向小张介绍员工的月工资实际水平更合理些;

(4)去掉四个管理人员的工资后,请你计算出其他员工的月平均工资y(结果保留整数),并判断y能否反映该公司普通员工的月工资实际水平。
26.(本题满分10分)
已知:如图,在梯形ABCD中,AD∥BC,AB=DC,点E、F、G分别在AB、BC、CD上,且AE=GF=GC
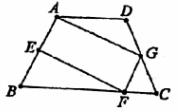
(1)求证:四边形AEFG是平行四边形;
(2)当∠FGC=2∠EFB时,求证:四边形AEFG是矩形。