2008-2009学年度冠县实验中学第二学期七年级期末学业水平评价
数学试题
第Ⅰ卷(选择题共48分)
一、选择题(本大题共l2个小题,每小题4分,在每小题给出的四个选项中,只有一项符合 题目要求)
1.若点A(x,3)与点B(2,y)关于x轴对称,则( )
A.x=一2,y=一3 B.x=2,y=
2.如图,下列结论中不正确的是( )
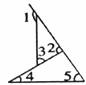
A.∠1=∠2+∠3 B.∠3=∠4+∠
3.已知方程组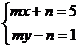 的解是
的解是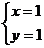 ,则m,n的值是( )
,则m,n的值是( )
A. B.
B. C.
C. D.
D.
4.如图,在下列给出的条件中,不能判定AB∥DF的是( )

A.∠A+∠2=180° B.∠1=∠4
C.∠A=∠3 D.∠1=∠A
5.下列事件不可能发生的是( )
A.打开电视机,CCTV一1正在播放新闻
B.我们班的同学将来会有人当选为劳动模范
C.在空气中,光的传播速度比声音的传播速度快
D.若实数C<0,则
6.一幅美丽的图案,在其顶点处由四个正多边形镶嵌而成,其中三个分别为正三角形、正四边形、正六边形,则另一个为( )
A.正三角形 B.正四边形 C.正五边形 D.正六边形
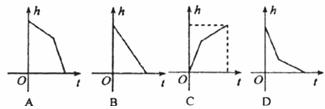
7.某蓄水池的横断面示意图如下图,如果这个注满水的蓄水池以固定的流量把水全部放出.下面的图象能大致表示水的深度h和放水时间t之间的关系的是( )
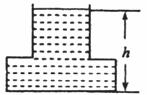
8.如图,∠A=32°,∠B=45°,∠C=38°,则∠DFE等于( )
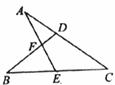
A.120° B.115° C.110° D.105°
9.如图,直线AB、CD相交于点O,OE平分∠BOC,OF⊥OE于O,若∠AOD=70°,则∠AOF等于( )

A.35° B.45° C.55° D.65°
10.如图,OB、OC是∠ABC、∠ACB的角平分线,∠BOC=140°,则∠A等于( )
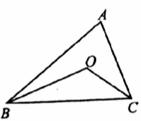
A.90° B.100° C.119° D.120°
11.下列四个算式:①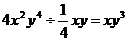 ;②
;②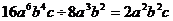 ;
;
③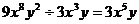 ;④
;④ ,其中正确的有( )
,其中正确的有( )
A.0个 B.1个 C.2个 D.3个
12.现有边长相等的正三角形、正方形、正六边形、正八边形的地砖,如果选择其中的两种铺满地面,那么选择的两种地砖形状不可能的是( )
A.正三角形与正方形 B.正三角形与正六边形
C.正方形与正六边形 D.正方形与正八边形
第Ⅱ卷 (非选择题共72分)
二、填空题(本大题共5个小题,每小题4分,共20分.只要求填写最后的结果)
13.设(xm-1yn+2)?(x5my-2)=x5y3,则nm的值为____________
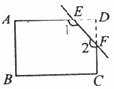
14.如图,一长方形纸片剪去一个角后,得到一个五边形ABCFE,则图中∠l+∠2=____度.
15.一次函数y=2x-6的图象与两坐标轴所围成的三角形的面积是___________.
16.若方程组 的解满足方程
的解满足方程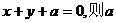 的值为_____________.
的值为_____________.
17.一个多边形除了一个内角外,其余各内角之和为l680°那么除去的这个内角的度数为___________.
三、解答题(本大题共6个小题,共52分.解答应写出必要的文字说明、推理过程或演算步骤)
18.(本题满分8分,每小题4分)
(1)[ab(3-b) b2)](
b2)](
(2)解方程组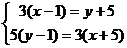
19.(本题满分8分)
如图,已知∠DAB+∠D=180°,AC平分∠D,且∠CAD=25°,∠B=95°

(1)求∠DCA的度数;
(2)求∠ACE的度数
20.(本题满分8分)
有两块试验田,原来可产花生470千克,改用良种后共产花生532千克,已知第一块田的产量比原来增加16%,第二块田的产量比原来增加10%,问这两块试验田改用良种后,各增产花生多少千克?
21.(本题满分8分)已知:如图,在△ABC中,D为BC上一点,∠1=∠2,∠3=∠4,∠BAC=120°,求∠DAC的度数.

22.(本题满分10分)
盒子里有标号为1,2,3的三个球,除标号不同外,其余均相同.任意取出两个球,求下列事件发生的概率.
(1)两个球的号码之和等于5;(2)两个球的号码之差等于2;
(3)两个球的号码之积为偶数;(4)两个球的号码之和为奇数.
23.(本题满分10分)
为了解菜地区土地沙化情况,环保部门对该地区进行了连续四年跟踪观测,所记录的近似数据如下表:
观测时间
第1年
第2年
第3年
第4年
沙漠面积
90万亩
90.2万亩
90,4万亩
90.6万亩
(1)根据表中提供的信息,在不采取任何措施的情况下,试定出该地区沙漠面积y(万亩)与x(年数)之间的关系式(用含x的式子表示y),并计算到第20年时该地区的沙漠面积;
(2)为了防沙治沙,政府决定投入资金,鼓励农民植树种草.经测算,植树1亩需资金200元,种草1亩需资金100元。某组农民计划在一年内完成2400亩绿化任务。在实施中,由于实际情况所限,植树完成了计划的90%,种草超额完成了计划的20%,恰好完成了计划的绿化任务,那么所节余的资金还能植树多少亩?