1．如果一元二次方程ax²+bx+c=0（a≠0）能用公式法求解，那么必须满足的条件是（    ）

A．b²-4acㄒ0    B．b²-4ac≤0       C．b²-4ac >0               D．b²-4ac<0

2．如果反比例函数y=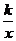的图象经过点P（-2，3），那么k的值是（    ）

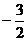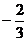A．6                 B．             C．                     D．-6

3．如图，所示的几何体的俯视图是（  ）

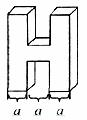
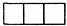A．         B．      C．           D．

4．用配方法解一元二次方程x²-4x+3=0时可配方得（    ）

A．（x-2）²=7                                B．（x-2）²=1

C．（x+2）²=1                           D．（x+2）²=2

5．已知菱形的边长为6cm，一个内角为60⁰，则菱形较短的对角线长为为（   ）

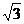A．6cm             B．6cm              C．3cm                D．3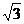m

6．在同一时刻，身高1.6米的小强在阳光下的影长为0.8米，一棵大树的影长为4.8米，则树的高度为（  ）

A．4.8米          B．6.4米                  C．9.6米           D．10米

7．某农机厂四月份生产零件50万个，第二季度共牛产零件182万个，设该厂五、六月份甲均每月的增长率为x，那么x满足的方程是（  ）

A．50（1+x）²=182                B．50+50（1+x）+50（1+x）²=182

C．50（1+2x）=182                  D．50+so（1+x、+50（1+2x）=182

8．如图，在△ABC中，AB=a，AC=b，BC边上的垂直平分线DE交BC、BA分别于点D、E，则△AEC的周长等于  （   ）

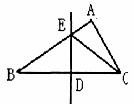
A．a+b              B．a-b               C．2a+b                      D．a+2b

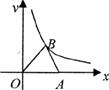
9．如图，在直角坐标系中，点A是x轴正半轴上的一个定点，点B是双曲线（x>0）上的一个动点，当点B的横坐标逐渐增大时，△OAB的面积将会（   ）

A．逐渐增大    B．不变             C．逐渐减小              D．先增大后减小

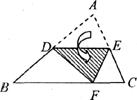
10．如图，将非等腰△ABC的纸片沿DE折叠后，使点A落在BC边上的点F处．若点D为AB边的中点，则下列结论：①△BDF是等腰三角形；②∠DFE=∠CFE；③DE是△ABC的中位线，成立的有（   ）

A．①②            B．①③            C．②③                      D．①②③

11．函数y=x+m与 （m≠0）在同一坐标系内的图象可以是（   ）

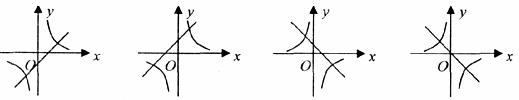
A                               B                               C                                 D

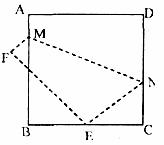
12．如图，将边长为8 cm的正方形ABCD折叠，使点D落在BC边的中点E处，点A落在F处，折痕为MN，则线段CN的长是（   ）

A．3cm             B．4cm             C．5cm                D．6cm 

13．已知x₁、x₂是方程x²-3x-2=0的两个实数根，则（x₁+2）（x₂+2）=_________

14．某等腰三角形的两条边长分别为3cm和6cm，则它的周长为_________cm。

15．已知反比例函数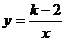的图象位于第一，第三象限．则k的取值范围是_________。

16．如图，在梯形ABCD中，AD∥BC，AB=CD，AC⊥BD，AD=6，BC=8，则梯形的高为_________。

17．已知点P是反比列函数y=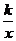（k≠0）的图像上任一点，过P点分别做x轴，y轴的平行线，若两平行线与坐标轴围成矩形的面积为2，则k的值为_________。

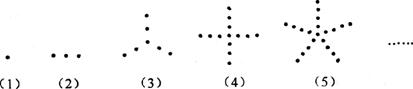
18．根据下列5个图形及相应点的个数的变化规律，试猜测第n个图中有_________个

点．

19．解方程（本题满分10分，每小题5分）

（1）x²-7x-18=0    （2）3x²+8x-3=0

20．如图，在△ABC中，AB=BC=12cm，∠ABC=80⁰，BD是∠ABC的平分线，DE∥BC．（本题满分8分）

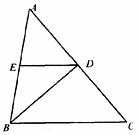
（1）求∠EDB的度数；

（2）求DE的长．

21．某商店购进一种商品，单价30元．试销中发现这种商品每天的销售量p（件）与每件的销售价x（元）满足关系：p=100-2x．若商店每天销售这种商品要获得200元的利润，那么每件商品的售价应定为多少元?每天要售出这种商品多少件?（本题满分10分）

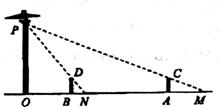
22．如图，路灯（P点）距地面8米，小明在距路灯的底部（O点）20米的A点时，测得此时他的影长AM为5米。

（1）求小明的身高；

（2）小明沿OA所在的直线行走14米到B点时，身影的长度是变长了还是变短了?变长或变短了多少米?（本题满分10分）

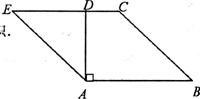
23．如图，在梯形ABCD中，AB∥DC，DA⊥AB，∠B=45⁰，延长CD到点E，使DE=DA，连接AE．（本题满分10分）

（1）求证：AE∥BC：

（2）若AB=3，CD=1，求四边形ABCE的面彩

24．已知：等腰△OAB在直角坐标系中的位置如图，点A的坐标为（-3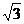；3），点B的坐标为（-6，0）．

（1）若△OAB关于y轴的轴对称图形是△OA’B’，请直接写出A、B的对称点A’、B’的坐标；

（2）若将△OAB沿x轴向右平移a个单位，此时点A恰好落在反比例函数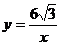的图像上，求a的值；

（3）若△OAB绕点O按逆时针方向旋转a度（0<a<90）．

①当a=30⁰时点B恰好落在反比例函数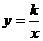的图像上，求k的值．

②问点A、B能否同时落在①中的反比例函数的图像上，若能，求出a的值；若不能，请说明理由．（本题满分12分）