2008-2009学年度博山第一学期初四期中教学质量诊断性检测
数学试题
一、填空题(每空3分,共36分)
1.在Rt△ABC中,∠C=90。,AC=5,BC=4,则tanA=_______.
2.如图,一架梯子斜靠在墙上,若梯子底端到墙的距离AC=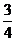 ,刚梯子长AB=_______米
,刚梯子长AB=_______米

3.已知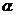 为锐角,则sin (900-
为锐角,则sin (900-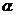 )-cos
)-cos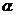 = _______
= _______
4.如图所示,某河堤的横断面是梯形ABCD,BC∥AD,迎水坡AB长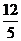 ,则河堤的高BE为_______米.
,则河堤的高BE为_______米.
5.当物体的某个面平行于投影面时,这个面的正投影与这个面的形状、大小_______.(填“相同”、“不一定相同”、“不相同”之一).
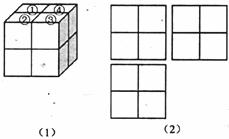
6.如图(1),用八个同样大小的小立方体搭成一个大立方体,小明从上面的四个小立方体中取走了两个后,得到的新几何体的三视图如图(2)所示,则他拿走的两个小立方体的序号是_______.(只填写满足条件的一种情况即可)
7.一天晚饭后,姐弟两人出去散步,经过一盏路灯时,弟弟突然高兴地对姐姐说:“我踩到你的‘脑袋’了”.可知两人中离这盏路灯较远的是_______.
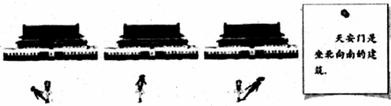
8.小华在不同时间于天安门前拍了几张照片,下面三张照片中最可能是小华在下午拍摄的为_______的一张.(请填写“左面”、“中间”或“右面”)
9.抛物线y=x2+x-4与y轴的交点坐标为_______.
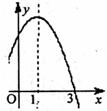
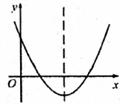
10.已知函数y=-x2+2x+c的部分图象如图所示,则当x_______ 时,y随x的增大而减小。
11.抛物线y=2x2+8x+m与x轴只有一个公共点,则m的值为_______
12.某题中,用“描点法”画二次函数y=ax2+bx+c的图象时,列了如下表格
x
…
-2
-1
0
1
2
…
y
…
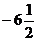
-4
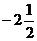
-2
…
根据表格上的信息回答问题:该二次函数y=ax2+bx+c在x=3时,y=_______.
二、选择逮(每小题4分,共40分)
1.cos600的值等于( )
A.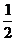 B.
B.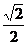 C.
C.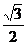 D.1
D.1
2.Rt△ABC中,∠C=900,BC= ,AC=
,AC=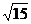 ,则∠A= ( )
,则∠A= ( )
A.900 B.
3.正方形网格中,∠AOB如图放置,则cos∠AOB的值为 ( )
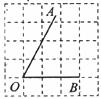
A. B.
B.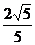 C.
C.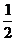 D.2
D.2
4.在△ABC,∠C=900,tanA=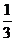 ,则sinB= ( )
,则sinB= ( )
A.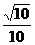 B.
B.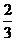 C.
C.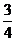 D.
D.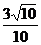
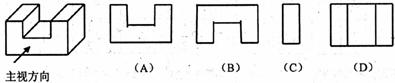
5.下图中三视图所对应的直观图是 ( )

6.图中所示几何体的俯视图是
7.二次函数y=(x-1)2 +2的最小值是 ( )
A.-2 B.
8.已知抛物线y=x2-x-1与x轴的一个交点为(m,0),那么代数式m2-m+2008值为 ( )
A.2006 B.
9.二次函数y=x2+4x+3的图像可以由二次函数y=x2的图像平移而得到,下列平移正确的是 ( )
A.先向左平移2个单位,再向上平移1个单位
B.先向左平移2个单位,再向下平移1个单位
C.先向右平移2个单位,再向上平移1个单位.
D.先向右平移2个单位,再向下平移1个单位
10.二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列说法不正确的是 ( )
A.b2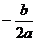 <0
<0
图(1)表示一个正六棱柱形状的高大建筑物,图(2)是它的俯视图.小明站在地面上观察该建筑物,当他在什么区域活动时,他只能同时看到其中三个侧面?请在图(2)中画出他所有可能的活动范围.
三、(本大题6±1分)

(1)一木杆按如图1所示的方式直立在地面上,请在图中画出它在阳光下的影子(用线段CD表示)
四、(本大题6±1分)
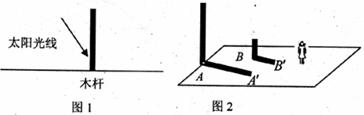
(2)图2是两根标杆及它们在灯光下的影子.请在图中画出光源的位置(用点P表示),并在图中画出人在此光源下的影子.(用线段即表示)
五、(本大题6±1分)
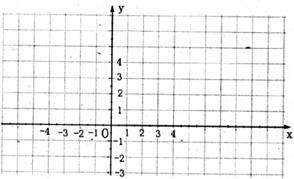
已知二次函数y1=ax2+bx+c(a≠0)的图像经过三点(1,0),(-3,0),(0,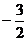 )求二次函数的解析式,并在给定的直角坐标系中作出这个函数的图像;
)求二次函数的解析式,并在给定的直角坐标系中作出这个函数的图像;
六、(本大题8±1分)。
如图,在梯形ABCD中,AD∥BC,∠B=900,AD=2,BC=5,tanC=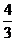 .
.
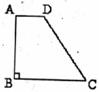
(1)求点D到BC边的距离;
(2)求点B到CD边的距离.
七、(本大题8±1分)
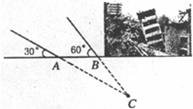
某地震救援队探测出某建筑物废墟下方点C处有生命迹象,已知废墟一侧地面上两探测点A、B相距3米,探测线与地面的夹角分别是300和600(如图),试确定生命所在点C的深度.(结果精确到0.1米,参考数据: ≈1.41,
≈1.41,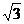 ≈l.73)
≈l.73)
八、(本大题10±1分)
王强在一次高尔夫球的练习中,在某处击球,其飞行路线满足抛物线y=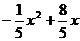 ,其中y(m)是球的飞行高度,x(m)是球飞出的水平距离,结果球离球洞的水平距离还有2m.
,其中y(m)是球的飞行高度,x(m)是球飞出的水平距离,结果球离球洞的水平距离还有2m.

(1)请写出抛物线的开口方向、顶点坐标、对称轴.
(2)请求出球飞行的最大水平距离.
(3)若王强再一次从此处击球,要想让球飞行的最大高度不变且球刚好进洞,则球飞行路线应满足怎样的抛物线,求出其解析式.