2008-2009学年度招远市第二学期初二第二学段测评
数学试题
说明:本试卷试题115分,书写质量3分,卷面安排2分,满分120分。
一、选择题(每小题2分,满分30分)
1.数据1,2,1,3,3的平均数为
A.1 B.2 C.3 D.10
2.下列从左边到右边的变形,是分解因式的为
A.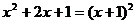 B.
B.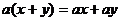
C.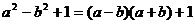 D.
D.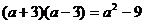
3.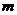 与3的和的一半是正数,用不等式表示为
与3的和的一半是正数,用不等式表示为
A.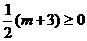 B.
B.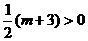
C.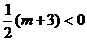 D.
D.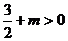
4.矩形两条对角线所夹锐角为60°,则矩形较短的边与较长的边的长度比是
A.1:1 B.1:2 C.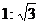 D.1:3
D.1:3
5.如下图,△ABC的面积为36,将△ABC沿BC平移到 ,使
,使 和C重合,连接
和C重合,连接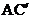 交
交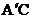 于点D,则
于点D,则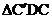 的面积为
的面积为
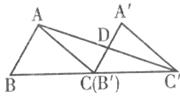
A.6 B.9 C.12 D.18
6.若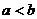 ,则下列不等式错误的是
,则下列不等式错误的是
A.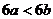 B.
B.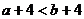 C.
C. D.
D.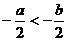
7.下列说法中错误的是
A.一组数据的平均数、众数和中位数可能是同一个数
B.一组数据的众数可能有多个
C.一组数据的中位数可能不唯一
D.众数、中位数和平均数是从不同的角度描述了一组数据的集中趋势
8.下列各式中,不含因式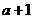 的是
的是
A.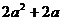 B.
B.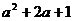 C.
C.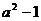 D.
D.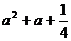
9.如下图,点E在正方形ABCD的边BC的延长线上,且CE=CA.AE与CD相交于点F,则∠AFC的度数为
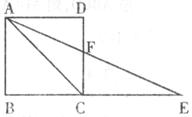
A.105° B.112.5° C.135° D.150°
10.某单位公务员的工资统计如下表:
工资(元)
1500
1800
2100
2300
2400
2600
人数
3
6
7
8
5
4
则这些公务员的工资的众数、中位数分别是
A.1800、2100 B.2100、2100 C.2300、2300 D.2100、2300
11.下列说法中正确的是
A.1是不等式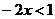 的解 B.1是不等式
的解 B.1是不等式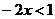 的解集
的解集
C.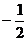 是不等式
是不等式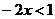 的解 D.不等式
的解 D.不等式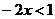 的解集是
的解集是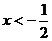
12.如下图,四边形ABCD是正方形,点F,G在正方形的边上,点E在CB的延长线上,BE=BF=DC。下列说法正确的是
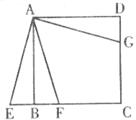
A.将△ADG绕点A按顺时针方向旋转得到△ABF
B.将△ADG绕点A按顺时针方向旋转得到△ABE
C.将△ABE平移得到△ABF
D.将△ADG平移得到△ABF
13.把多项式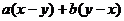 分解因式的结果是
分解因式的结果是
A.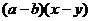 B.
B.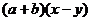
C.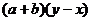 D.
D.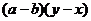
14.如下图,用8个全等的等腰梯形镶嵌成一个平行四边形ABCD,刚AD:AB等于
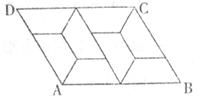
A.1:2 B.3: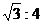 D.2:3
D.2:3
15.若关于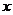 的不等式组
的不等式组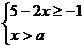 无解,则
无解,则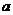 的取值范围是
的取值范围是
A.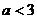 B.
B.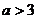 C.
C.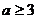 D.
D.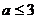
二、填空题(将正确答案填在横线上,每小题3分,满分30分)
16.2008年北京奥运会,射箭女子个人决赛张娟娟创历史首夺金牌,她在决赛中的射击成绩为(单世:环):10,7,9,9,9,9,10,9,10,10,9,9。则这组数据的众数为_____。
17.写出一个解集为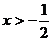 的不等式___________。
的不等式___________。
18.若一个正方形的面积为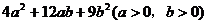 ,则这个正方形的边长为___________。
,则这个正方形的边长为___________。
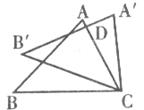
19.如下图,把△ABC绕着点C顺时针旋转35°,得到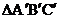 ,
,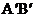 交AC于点D,若
交AC于点D,若 ,则∠A的度数是___________。
,则∠A的度数是___________。
20.不等式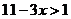 的最大整数解是___________。
的最大整数解是___________。
21.若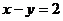 ,
,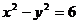 ,则
,则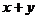 的值是___________。
的值是___________。
22.如下图,□ABCD中,DB=DC,∠A=65°,CE⊥BD于点E,则∠BCE的度数为_________。

23.规范办学行为以来,某校规定:学生的平时作业、期中测评、期末测评三项成绩分别按2:1:2的比计入学期总成绩。小明的平时作业、期中测评、期末测评的数学成绩依次为95分、93分、90分,则小明这学期的数学总成绩是___________分。
24.如下图,在梯形ABCD中,AD∥BC,对角线AC⊥BD,若AC=8cm,BD=6cm,则此梯形高的长为___________。
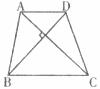
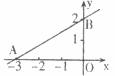
25.如下图,一次函数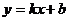 的图像与坐标轴的交点为A(-3,0)和B(0,2),则不等式
的图像与坐标轴的交点为A(-3,0)和B(0,2),则不等式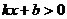 的解集为___________。
的解集为___________。
三、解答题(每题10分,满分20分)
26.(1)解不等式: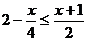 ,并把它的解集表示在数轴上。
,并把它的解集表示在数轴上。
(2)解不等式组: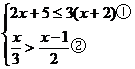
27.把下列各式分解因式:
(1)
(2)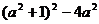
四、解释与说明题(每题8分,满分16分)
28.为了从甲、乙两名同学中选拔一人参加电脑知识竞赛,在相同条件下对他们的电脑知识进行了10次测验,成绩如下表:(单位:分)
甲
76
84
90
86
81
87
86
82
85
93
乙
82
84
85
89
79
80
91
89
74
79
回答下列问题:
(1)甲同学成绩的众数是_________分,乙同学成绩的中位数是_________分;
(2)若测验分数在85分以上(含85分)为优秀,则甲同学的优秀率为_________,乙同学的优秀率为_________;
(3)若甲同学成绩的平均数为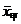 ,乙同学成绩的平均数为
,乙同学成绩的平均数为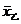 ,则有
,则有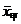 _________
_________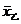 (填“>”、“<”或“=”);
(填“>”、“<”或“=”);
(4)综合以上数据,你认为应该派哪一名同学参加电脑知识竞赛?并说明理由。
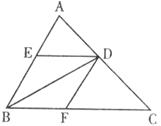
29.如下图,BD是△ABC的角平分线,DF∥AB交BC于F,DE∥BC交AB于E。试猜想四边形DEBF是何种特殊的平行四边形?并说明你的理由。
五、探索题(满分8分)
30.观察下列等式:
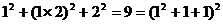 ,
,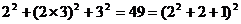 ,
,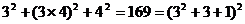 ,
,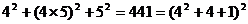 ,
,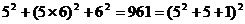 ,……
,……
(1)根据以上运算,你发现了什么规律,用含有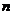 (
(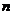 为正整数)的等式表示该规律;
为正整数)的等式表示该规律;
(2)请用分解因式的知识说明你发现的规律的正确性。
六、实际应用题(满分11分)
31.某房地产开发公司计划建A、B两种户型的住房共80套,已知该公司所筹资金不少于2090万元,但不超过2096万元,且所筹资金全部用于建房两种户型的建房成本和售价如下表:
户型
A
B
成本(万元/套)
25
28
售价(万元/套)
30
34
(1)该公司对这两种户型住房有几种建房方案?请写出所有方案;
(2)该公司如何建房可获得最大利润?最大利润是多少?(利润=售价-成本)