2008-2009学年度遂宁市蓬溪县第一学期八年级期末教学质量检测
数学试题
说明:本试题满分150分,考试时间120分钟。
一、选择题(四择一,每小题3分,共60分)
1.代数式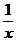 ,
,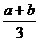 ,
,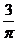 ,
, ,
,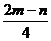 中,分式有
中,分式有
A.1个 B.2个 C.3个 D.4个
2.下列计算正确的是
A.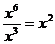 B.
B.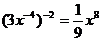 C.
C.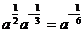 D.
D.
3.在函数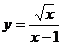 等中,自变量
等中,自变量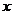 的取值范围是
的取值范围是
A.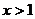 B.
B.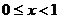 C.
C.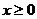 且
且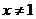 D.
D.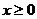
4.点P(3,2)关于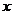 轴的对称点
轴的对称点 的坐标是( )
的坐标是( )
A.(3,-2) B.(-3,2) C.(-3,-2) D.(3,2)
5.若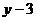 与
与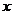 成反比例,且当
成反比例,且当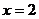 时,
时,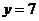 ,则
,则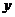 与
与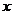 之间的函数关系式是
之间的函数关系式是
A.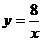 B.
B.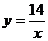 C.
C.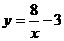 D.
D.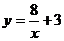
6.已知正比例函数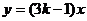 ,若
,若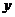 随
随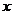 的增大而增大,则
的增大而增大,则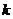 的取值范围是
的取值范围是
A.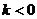 B.
B. C.
C. D.
D.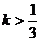
7.若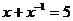 ,则
,则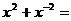
A.23 B.
8.如下图:在△ABC中,点E、D、F分别在AB、BC、AC上且DE∥CA,DF∥BA,下列四个判断中不正确的是
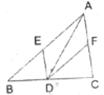
A.四边形AEDF是平行四边形
B.如果∠BAC=90°,那么四边形AEDF是矩形
C.如果AD⊥BC,那么四边形AEDF是菱形
D.如果AD平分∠BAC,那么四边形AEDF是菱形
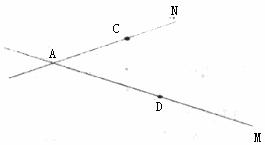
9.如下图:直线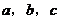 表示三条相互交叉环湖而建的公路,现建立一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有
表示三条相互交叉环湖而建的公路,现建立一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有
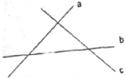
A.1个 B.2个 C.3个 D.4个
10.一件工作,甲单独做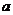 小时完成,乙单独做
小时完成,乙单独做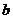 小时完成,那么甲乙两人合做需要( )小时完成。
小时完成,那么甲乙两人合做需要( )小时完成。
A.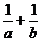 B.
B. C.
C.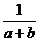 D.
D.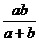
11.一组数据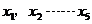 的方差是3,那么另一组数据
的方差是3,那么另一组数据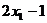 ,
,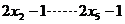 的方差是
的方差是
A.3 B.
12.四边形ABCD的对角线AC,BD相交于点O,能判定它为正方形的题设是
A.AO=CO,BO=DO B.AO=CO=BO=DO
C.AO=CO,BO=DO,AC⊥BD D.AO=BO=CO=DO,AC⊥BD
13.下列各命题中,其逆命题是真命题的是
A.如果 都是正数,那么它们的积
都是正数,那么它们的积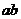 也是正数
也是正数
B.等边三角形是等腰三角形
C.全等三角形的面积相等
D.线段垂直平分线上的点到这条线段两端点的距离相等
14.某人早上进行登山活动,从山脚到山顶休息一会儿又沿原路回,若横轴表示时间 ,纵轴表示与山脚的距离
,纵轴表示与山脚的距离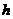 ,则下面四个图中反映全程
,则下面四个图中反映全程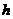 与
与 的关系图是
的关系图是

15.刘翔为了迎战2008年北京奥运会刻苦进行
A.平均数 B.中位数 C.众数 D.方差
16.小明五次跳远的成绩是:3.6,3.8,4.2,4.0,3.9,这组数据的中位数是
A.3.9 B.
17.用尺规作图,不能作出唯一三角形的是
A.已知两角和夹边 B.已知两边和其中一边的对角
C.已知两边和夹角 D.已知两角和其中一角的对边
18.□ABCD的两邻边AB=4,AD=3,则对角线AC的取值范围是
A.AC>1 B.AC<
19.如果最简二次根式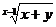 与
与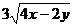 是同类二次根式,则
是同类二次根式,则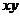 的值为
的值为
A.5 B.-
20.若 ,则
,则 的值为
的值为
A.-6 B.
二、填空题(2分×10=20分)
21.平行四边形ABCD中,AC与BD交于O,则其中共有________对全等的三角形。
22.空气的密度为
23.某地区某日气温的极差为
24.将直线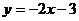 向上平移2个单位,得到直线________。
向上平移2个单位,得到直线________。
25.函数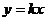 的图像过点(2,6)及点(
的图像过点(2,6)及点(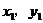 )和(
)和(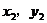 ),则当
),则当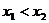 时,
时, 。
。
26.在△ABC中,AB=
27.若方程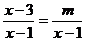 有增根,则
有增根,则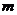 的值为________。
的值为________。
28.化简 的结果为________。
的结果为________。
29.已知:∠BAC=130°,若MP和NQ分别是AB、AC的中垂线,则∠PAQ=_______度。
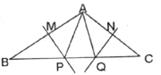
30.把命题“对顶角相等。”改写成:“如果…,那么…”的形式是________。
三、解答下列各题(共70分,其中31题前4个小题每题4分,其余各题分数见题号处)
31.计算:(1)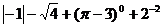
(2)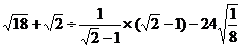
(3)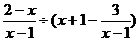
(4)解分式方程: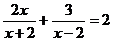
(5)(6分)先化简再求值: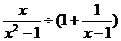 ,其中
,其中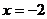
32.(7分)某工厂计划生产机床300台,生产了60台后,引入高科技,每天生产的台数是原来的1.2倍,结果提前4天完成了任务,求原计划每天生产机床多少台?
33.(7分)小明同学骑自行车去郊外春游,下图表示他离家的距离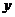 (千米)与所用的时间
(千米)与所用的时间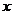 (小时)之间关系的函数图像。
(小时)之间关系的函数图像。
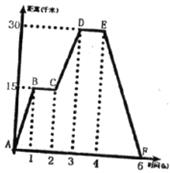
(1)根据图像回答:小明到达离家最远的地方用了几小时?此时离家多远?(2分)
(2)求小明从家出发后两个半小时离家多远?(2分)
(3)求小明何时距家
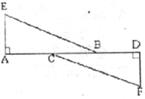
34.(6分)如下图,点A、B、C、D在同一直线上,AE⊥AD,FD⊥AD,垂足分别为A、D,AE=DF,AC=BD,求证:BE=CF。
35.(6分)如下图,已知AM、AN是两条交叉的公路,D、C分别是公路旁的两个村庄,现要修建一个水塔,使它到两条公路的距离相等,到两个村庄的距离也相等,请你作出水塔P的位置。(要求:不写作法:保留作图痕迹。)
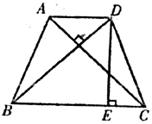
36.如下图,已知等腰梯形ABCD中,AD∥BC,对角线AC⊥BD,AD=
37.(6分)某学校为了解该校七年级学生的身高情况,抽样测查了部分同学,将所得数据处理后,制成扇形统计图和频数分布直方图(部分)如下(每组只含最低值不含最高值,身高单位:cm,测量时精确到
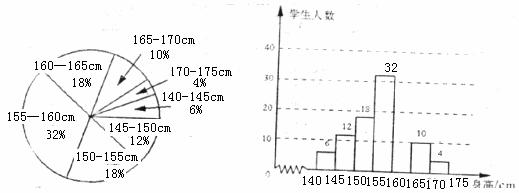
(1)请根据所提供的信息补全频数分布直方图;(2分)
(2)样本的中位数在统计图的哪个范围内?(2分)
(3)如果上述样本的平均数为
38.(10分)某影碟出租店开设两种租碟方式:一种是零星租碟,每张收费1元,另一种是会员卡租碟,办卡费每月12元,租碟每张0.4元,小郑经常来该店租碟。若每月租碟数量为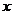 张。
张。
(1)分别写出零星租碟方式每月应付金额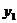 元和会员卡租碟方式每月应付金额
元和会员卡租碟方式每月应付金额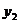 元与租碟数量
元与租碟数量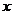 张之间的函数关系式。(4分)
张之间的函数关系式。(4分)
(2)若小郑计划7月份租碟30张,问选择哪种租碟方式省钱,计算说明。(4分)
(3)当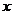 为何值时,采用零星租碟合算?(2分)
为何值时,采用零星租碟合算?(2分)