2008-2009学年度定陶县第二学期七年级期中学业水平测试
数学试卷
一、精挑细选,火眼金睛(每小题3分,共30分)
1.如下图,能用∠1,∠O,∠AOB三种方法表示同一个角的是
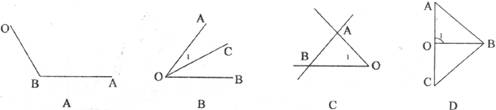
2.从甲处看乙,乙在北偏西40°,那么从乙处看甲,则甲在
A.南偏东40° B.南偏西40° C.南偏东50° D.南偏西50°
3.8点30分时针与分针的夹角为
A.85° B.75° C.70° D.60°
4.如下图,直线AE∥CD,∠EBF=135°,∠BFD=60°,则∠FDC等于
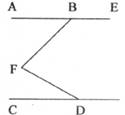
A.75° B.45° C.30° D.15°
5.一学员在广场上练习驾驶汽车,两次拐弯后,行驶方向与原来方向相同,这两次拐弯的角度可能是
A.第一次向左拐50°,第二次向左拐130°
B.第一次向右拐40°,第二次向右拐40°
C.第一次向左拐40°,第二次向右拐140°
D.第一次向左拐40°,第二次向右拐40°
6.点C在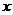 轴上方,
轴上方,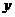 轴左侧,距离
轴左侧,距离 轴3个单位长度,距离
轴3个单位长度,距离 轴4个单位长度,则点C坐标为
轴4个单位长度,则点C坐标为
A.(3,4) B.(-3,-4) C.(-4,3) D.(4,-3)
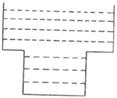
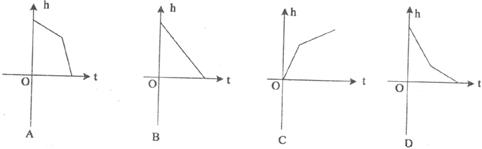
7.某蓄水池的横断面示意图如下图,分深水区与浅水区,如果这个注满水的蓄水池以固定的流量把水全部放出,下面的图像能大致表示水的深度h,与放水时间t之间的关系是
8.关于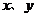 的二元一次方程
的二元一次方程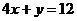 ,
,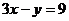 ,
,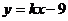 有公共解,则
有公共解,则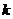 的值是
的值是
A.4 B.
9.已知代数式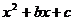 ,当
,当 时,它的值是2,当
时,它的值是2,当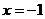 时,它的值是8,则
时,它的值是8,则 的值是
的值是
A.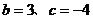 B.
B.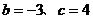
C.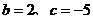 D.
D.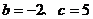
10.某商场搞优惠活动,决定由顾客抽奖确定折扣,某顾客购买甲、乙两种商品,分别抽到七折和九折,共付款386元,若这两种商品原价之和为500元,若设甲商品原价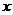 元,乙商品原价为
元,乙商品原价为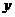 元,则列出的方程组为
元,则列出的方程组为
A.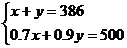 B.
B.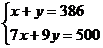
C.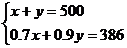 D.
D.
二、画龙点睛,一锤定音!(每小题3分,共36分)
11.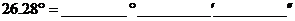 ,
,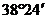 的余角为_________,补角为_________。
的余角为_________,补角为_________。
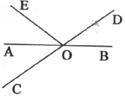
12.如下图,直线AB,CD相交于O点,OA平分∠EOC,且∠EOC=76°,则∠BOD的度数为_________。
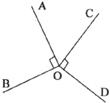
13.如下图,OA⊥OB,OC⊥OD,∠AOC┱∠BOD=1┱2,则∠BOD=_________。
14.如果点(-1,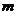 )与(2,
)与(2,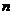 )都在直线
)都在直线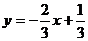 的图像上,则
的图像上,则 (填“>”“<”号)
(填“>”“<”号)
15.若点P( ,
,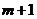 )在平面直角坐标系的
)在平面直角坐标系的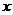 轴上,则P点坐标为_________。
轴上,则P点坐标为_________。
16.已知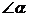 与
与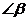 是两条平行线被第三条直线所截得的同旁内角,如果
是两条平行线被第三条直线所截得的同旁内角,如果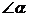 比
比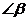 的2倍还大30°,则
的2倍还大30°,则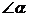 =_________,
=_________,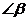 =_________。
=_________。
17.如果P(-2,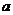 )是正比例函数
)是正比例函数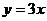 图像上一点,则
图像上一点,则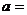 _________。
_________。
18.如果一个角的两边与另一角的两边相互平行,则两个角的关系是_________。
19.如果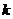 能使方程组
能使方程组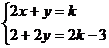 的解中,
的解中,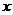 与
与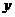 的和为0,则
的和为0,则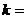 _________。
_________。
20.将一些科技读物分给若干个学生;若每个学生分6本,则剩下4本,若每个学生分7本,则差2本,则共有_________个学生、共_________本科技读物。
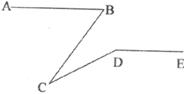
21.已知AB∥DE,∠ABC=60°,∠CDE=140°,则∠BCD=_________。
22.在∠AOE内部,
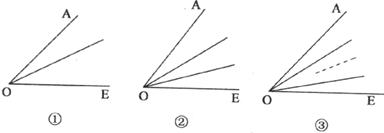
(1)如果从点O出发引一条射线,图中共有_________个角。
(2)如果从O点出发引出两条射线,图中共有_________个角。
(3)如果从O点出发引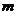 条射线,图中共有_________个角。(用含
条射线,图中共有_________个角。(用含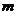 的式子表示)
的式子表示)
三、妙笔生花,挑战自我(共54分)
23.(8分)解方程组
(1)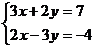
(2)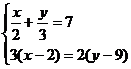
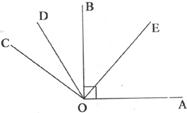
24.(6分)如图,∠AOE=∠BOE,∠BOD=∠COD,OB⊥OA,且∠EOD=75°,求∠BOC的度数。
25.(9分)如图,OBCD为正方形
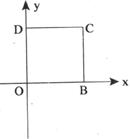
(1)如果B点坐标为(4,0),请写出其它三个顶点的坐标。
(2)如果将正方形向左平移3个单位,再向下平移1个单位,那么各顶点平移后的坐标是什么?
(3)如果这个正方形平移后0点坐标为(2,-1),则其余各顶点坐标为多少?请分别写出来。
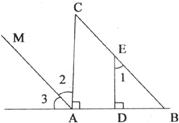
26.(8分)如下图,CA⊥AB于A,ED⊥AB于D,∠3=∠B,试判断:∠1与∠2的大小关系,并说明理由。
27.(8分)某市种植某种绿色蔬菜,全部用来出口,为了扩大出口规模,该市决定对这种蔬菜的种植进行政府补贴,规定每种一亩一次性补贴菜农若干元,经调查,种植亩数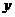 (亩)与补贴数额
(亩)与补贴数额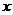 (元)之间大致满足如下图所示的一次函数关系。
(元)之间大致满足如下图所示的一次函数关系。
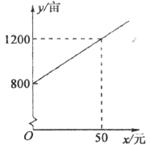
试求:(1)此一次函数的解析式;
(2)当补贴数额为60元时,种植这种蔬菜的亩数为多少?
28.(7分)某市2007年秋季开始,减免学生在义务教育阶段的学杂费,并按照每学期小学每生250元,初中每生450元的标准,由财政拨付学校作为办公经费,该市一学校小学生和初中生共有840人,2007年秋季收到当学期该项拨款29000元,该校小学生、初中生各有多少人?
29.(8分)对于一次函数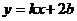 ,
,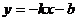 ,若两函数图像的交点为P(-3,2)。
,若两函数图像的交点为P(-3,2)。
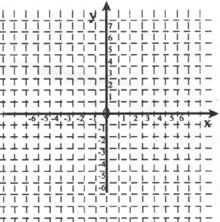
试求:(1)这两个一次函数的解析式;
(2)两函数图像与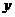 轴所围成的三角形的面积?
轴所围成的三角形的面积?