2009年北京市门头沟区初三第一次统一练习
数学试卷
一、选择题(共8道小题,每小题4分,共32分)
1.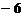 的相反数等于
的相反数等于
A.6
B.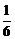 C.
C.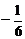 D.
D.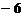
2.“地球一小时”是世界自然基金会向全球发出的熄灯环保活动,呼吁个人、社区、企业和政府共同参与到地球的节能环保活动中.据称,全球如果有1亿家庭关灯一个小时,就将减少550000吨二氧化碳的排放.将550000用科学记数法表示应为
A.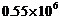 B.
B.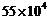 C.
C.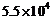 D.
D.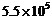
3.在函数 中,自变量x的取值范围是
中,自变量x的取值范围是
A.x≠3
B.x≥
4.如图所示的几何体的主视图是

5.把多项式xy2-16x分解因式,结果正确的是
A.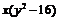 B.
B.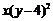 C.
C.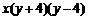 D.
D.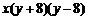
6.如图,AB是⊙O的弦,OD⊥AB,垂足为C,交⊙O于点D,点E在⊙O上.若
∠BED=30°,⊙O的半径为4,则弦AB的长是
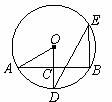
A.4 B.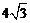 C.2
D.
C.2
D.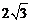
7.有6张形状、大小、质地均相同的卡片,正面分别印有数字1、2、3、4、5、6,背面完全相同.现将这6张卡片洗匀后正面向下放在桌子上,从中随机抽取一张,抽出的卡片正面印有的数字是偶数的概率是
A.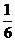 B.
B.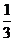 C.
C.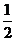 D.
D.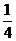
8.如下图,是一个棱长为2的正方体,一只蜘蛛在顶点A处,一只小昆虫在顶点B处,则蜘蛛接近小昆虫时所爬行的最短路线的长是
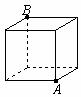
A.6
B.2+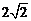 C.
C.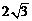 D.
D.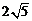
二、填空题(共4道小题,每小题4分,共16分)
9. 化简: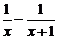 =
.
=
.
10.若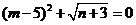 ,则mn的值为
.
,则mn的值为
.
11.某学习小组7名同学一周参加体育锻炼的时间分别是(单位:小时):6,7,6,8,9, 8,9,这组数据的中位数是 .
12.如下图,每个多边形的边长都大于2,分别以多边形的各顶点为圆心,1为半径画弧(弧的端点分别在多边形的相邻两边上),则第6个图形中所有弧的弧长的和是 ,第n个图形中所有弧的弧长的和是 (n为正整数).
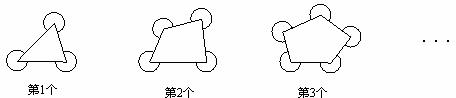
三、解答题(共5道小题,共25分)
13.(本小题满分5分)
计算: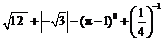 .
.
14.(本小题满分5分)
解不等式组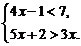
15.(本小题满分5分)
已知:如图,B、C、E三点在同一条直线上,AC∥DE,AC=CE,∠ACD=∠B.
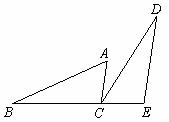
求证:BC=DE.
16.(本小题满分5分)
已知 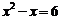 ,求代数式
,求代数式 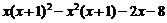 的值.
的值.
17.(本小题满分5分)
已知一次函数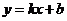 的图象与反比例函数
的图象与反比例函数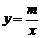 的图象交于A(-2,1)、B(1,n)两点.
的图象交于A(-2,1)、B(1,n)两点.
(1)求反比例函数的解析式和B点的坐标;
(2)在同一直角坐标系中画出这两个函数图象的示意图,并观察图象回答:当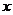 为何
值时,一次函数的值大于反比例函数的值?
为何
值时,一次函数的值大于反比例函数的值?
(3)直接写出将一次函数的图象向右平移1个单位长度后所得函数图象的解析式.
四、解答题(共2道小题,共10分)
18.(本小题满分5分)
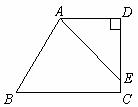
已知:如图,在梯形ABCD中,AD//BC,∠D=90°,∠B=60°,CD=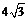 ,BC=9,cos∠DAE=
,BC=9,cos∠DAE=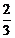 ,求AE的长.
,求AE的长.
19.(本小题满分5分)
已知:如图,AB是⊙O的直径,E是AB延长线上的一点,D是⊙O上的一点,且AD平分∠FAE,ED⊥AF交AF的延长线于点C.
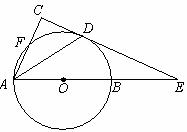
(1)判断直线CE与⊙O的位置关系,并证明你的结论;
(2)若AF∶FC=5∶3,AE=16,求⊙O的直径AB的长.
五、解答题(本题满分5分)

请你根据以上信息解答下列问题:
21.(本小题满分5分)列方程或方程组解应用题:
在学校开展的为偏远贫困地区的少年儿童捐献文具的活动中,甲、乙两班共捐献文具260件,已知甲班有40人参加了此次活动,乙班有35人参加了此次活动,且乙班人均捐献文具的件数是甲班人均捐献文具件数的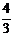 倍,问甲、乙两班各捐献文具多少件?
倍,问甲、乙两班各捐献文具多少件?
22.(本小题满分5分)
如图所示,有两种形状不同的直角三角形纸片各两块,其中一种纸片的两条直角边长都为3,另一种纸片的两条直角边长分别为1和3.图1、图2、图3是三张形状、大小完全相同的方格纸,方格纸中的每个小正方形的边长均为1.
(1)请用三种方法(拼出的两个图形只要不全等就认为是不同的拼法)将图中所给四块直角三角形纸片拼成平行四边形(非矩形),每种方法要把图中所给的四块直角三角形纸片全部用上,互不重叠且不留空隙,并把你所拼得的图形按实际大小画在图1、图2、图3的方格纸上(要求:所画图形各顶点必须与方格纸中的小正方形顶点重合;画图时,要保留四块直角三角形纸片的拼接痕迹);
(2)三种方法所拼得的平行四边形的面积是否是定值?若是定值,请直接写出这个定值;若不是定值,请直接写出三种方法所拼得的平行四边形的面积各是多少;
(3)三种方法所拼得的平行四边形的周长是否是定值?若是定值,请直接写出这个定值;若不是定值,请直接写出三种方法所拼得的平行四边形的周长各是多少.
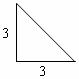

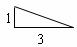




图1 图2 图3
七、解答题(本题满分7分)
23.已知以x为自变量的二次函数y=x2+2mx+m-7.
(1)求证:不论m为任何实数,二次函数的图象与x轴都有两个交点;
(2)若二次函数的图象与x轴的两个交点在点(1,0)的两侧,关于x的一元二次方程m2x2+(
(3)在(2)的条件下,关于x的另一方程 x2+2(a+m)x+
八、解答题(本题满分7分)
24.在平面直角坐标系xOy中,抛物线 y=-x2+bx+c与x轴交于A、B 两点(点A在点B的左侧),与y轴交于点C,顶点为D,且点B的坐标为(1,0), 点C的坐标为(0,3).
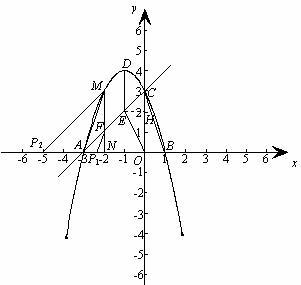
(1)求抛物线及直线AC的解析式;
(2)E、F是线段AC上的两点,且∠AEO=∠ABC,过点F作与y轴平行的直线交抛物线于点M,交x轴于点N.当MF=DE时,在x轴上是否存在点P,使得以点P、A、F、M为顶点的四边形是梯形? 若存在,请求出点P的坐标;若不存在,请说明理由;
(3)若点Q是位于抛物线对称轴左侧图象上的一点,试比较锐角∠QCO与∠BCO 的大小(直接写出结果,不要求写出求解过程,但要写出此时点 Q的横坐标x的取值范围).
九、解答题(本题满分8分)
25.如图1,在△ACB和△AED中,AC=BC,AE=DE,∠ACB=∠AED=90°,点E在AB上, F是线段BD的中点,连结CE、FE.
(1)请你探究线段CE与FE之间的数量关系(直接写出结果,不需说明理由);
(2)将图1中的△AED绕点A顺时针旋转,使△AED的一边AE恰好与△ACB的边AC在同一条直线上(如图2),连结BD,取BD的中点F,问(1)中的结论是否仍然成立,并说明理由;
(3)将图1中的△AED绕点A顺时针旋转任意的角度(如图3),连结BD,取BD的中点F,问(1)中的结论是否仍然成立,并说明理由.