2008-2009学年度北京市宣武区第二学期九年级第一次质量检测
数学试卷
一、选择题(共8个小题,每小题4分,共32分)
1. 的相反数是
(
)
的相反数是
(
)
A.3
B. C.
C. D.
D.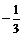
2.2008年北京市经济保持较快发展,按常住人口计算,全市人均GDP达到63029元,这个数据用科学记数法表示为 ( )
A.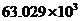 元
B.
元
B. 元
元
C. 元
D.
元
D.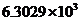 元
元
3.⊙O的半径为 ,圆心O到直线
,圆心O到直线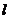 的距离为
的距离为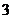 ,则直线
,则直线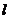 与⊙O的位置关系是 ( )
与⊙O的位置关系是 ( )
A.相交 B. 相切 C. 相离 D.无法确定
4.如图,AB、CD相交于点O,∠1=80°,如果DE∥AB,那么∠D的度数为 ( )
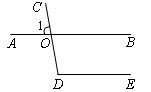
A.110° B.100° C.90° D.80°
5.如图是小敏同学6次数学测验的成绩统计图,则该同学6次成绩的中位数是 ( )

A.60分 B.70分 C.75分 D.80分
6.乌鸦口渴到处找水喝,它看到了一个装有水的瓶子,但水位较低,且瓶口又小,乌鸦喝不着水,沉思一会儿后,聪明的乌鸦衔来一个个小石子放入瓶中,水位上升后,乌鸦喝到了水。在这则乌鸦喝水的故事中,设从乌鸦看到瓶的那刻起向后的时间为 ,瓶中水位的高度为
,瓶中水位的高度为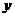 ,下列图象中最符合故事情景的是
( )
,下列图象中最符合故事情景的是
( )

7.如图是某几何体的三视图及相关数据,则判断正确的是 ( )

A.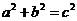 B.
B.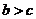 C.
C.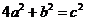 D.
D.
8.任何一个正整数 都可以进行这样的分解:
都可以进行这样的分解: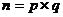 (
( 是正整数,且
是正整数,且 ),如果
),如果 在
在 的所有这种分解中两因数之差的绝对值最小,我们就称
的所有这种分解中两因数之差的绝对值最小,我们就称 是
是 的最佳分解,并规定:
的最佳分解,并规定: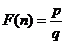 .例如
.例如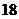 可以分解成
可以分解成 、
、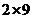 或
或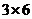 ,这时就有
,这时就有 .给出下列关于
.给出下列关于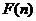 的说法:(1)
的说法:(1) ;(2)
;(2)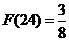 ;(3)
;(3) ;(4)若
;(4)若 是一个完全平方数,则
是一个完全平方数,则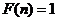 .其中正确说法的个数是( )
.其中正确说法的个数是( )
A.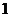 B.
B.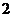 C.
C.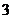 D.
D.
二、填空题(共4个小题,每小题4分,共16分)
9.某商场为了解本商场服务质量,随机调查了来本商场的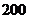 名顾客,调查的结果如图所示,根据图中给出的信息,这
名顾客,调查的结果如图所示,根据图中给出的信息,这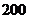 名顾客中对该商场的服务质量表示不满意的有_________名.
名顾客中对该商场的服务质量表示不满意的有_________名.

10.将抛物线 的图象向右平移3个单位,则平移后的抛物线的解析式为 __ _.
的图象向右平移3个单位,则平移后的抛物线的解析式为 __ _.
11.已知关于 的一元二次方程
的一元二次方程  有两个不相等的实数根 ,则
有两个不相等的实数根 ,则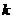 的取值范围是 ___
___.
的取值范围是 ___
___.
12.如图,在梯形ABCD中,AB∥DC,AB⊥BC,AB=

三、解答题(共5个小题,共25分)
13.(本小题满分5分)
计算: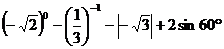 .
.
14.(本小题满分5分)
解不等式组:
15.(本小题满分5分)
如图,在 ABCD
ABCD 中,点E是AD的中点,BE的延长线与CD的延长线相交于点F.
中,点E是AD的中点,BE的延长线与CD的延长线相交于点F.
(1)求证:△ABE ≌△DFE;
(2)连结BD、AF,请判断四边形ABDF的形状,并证明你的结论.

16.(本小题满分5分)
如图,一次函数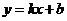 的图象与反比例函数
的图象与反比例函数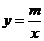 的图象交
的图象交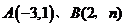 于两点,直线
于两点,直线 分别交
分别交 轴、
轴、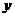 轴于
轴于 两点.
两点.
(1)求上述反比例函数和一次函数的解析式;
(2)求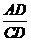 的值.
的值.

17.(本小题满分5分)
先化简,再求值: ÷x,其中x=
÷x,其中x= .
.
四、解答题(共2个小题,共10分)
18.(本小题满分5分)
小明在复习数学知识时,针对“求一元二次方程的解”,整理了以下的几种方法,请你将有关内容补充完整:
例题:求一元二次方程 的两个解.
的两个解.
解法一:选择合适的一种方法(公式法、配方法、分解因式法)求解.
解方程: .
.
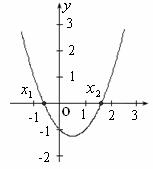
解法二:利用二次函数图象与坐标轴的交点求解.
如图1所示,把方程 的解看成是二次函数
的解看成是二次函数 的图象与
的图象与 轴交点的
轴交点的 横坐标,即
横坐标,即 就是方程的解.
就是方程的解.
解法三:利用两个函数图象的交点求解.
(1)把方程 的解看成是一个二次函数
的解看成是一个二次函数 的图象与一个一次函数
的图象与一个一次函数 的图象交点的横坐标;
的图象交点的横坐标;
 (2)画出这两个函数的图象,用
(2)画出这两个函数的图象,用 在
在 轴上标出方程的解.
轴上标出方程的解.
19.(本小题满分5分)
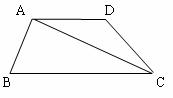
如图,在梯形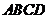 中,
中, ∥
∥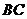 ,
, ⊥
⊥ ,
, ,
, =
=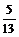 ,
, .
.
求(1)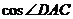 的值;(2)线段
的值;(2)线段 的长.
的长.
五、解答题(本题满分6分)
20.在物理实验中,当电流在一定时间段内正常通过电子元件 时,每个电子元件的状态有两种可能:通电或断开,并且这两种状态的可能性相等.
时,每个电子元件的状态有两种可能:通电或断开,并且这两种状态的可能性相等.

(1) 如图1,当只有1个电子元件时,P、Q之间电流通过的概率是 ___________;
(2) 如图2,当有2个电子元件a、b并联时,请你用树状图(或列表法)表示图中P、Q 之间电流能否通过的所有可能情况,并求出P、Q之间电流通过的概率;
(3) 如图3,当有3个电子元件并联时,P、Q之间电流通过的概率是__________.
六、解答题(共2个小题,共9分)
21.(本小题满分5分)
列方程(组)或不等式(组)解应用题:
某商场用36万元购进A、B两种商品,销售完后共获利6万元,其进价和售价如下表:
A
B
进价(元/件)
1200
1000
售价(元/件)
1380
1200
(注:获利 = 售价 ― 进价)
(1)该商场购进A、B两种商品各多少件;
(2)商场第二次以原进价购进A、B两种商品.购进B种商品的件数不变,而购进A种商品的件数是第一次的2倍,A种商品按原售价出售,而B种商品打折销售.若两种商品销售完毕,要使第二次经营活动获利不少于81600元,B种商品最低售价为每件多少元?
22.(本小题满分4分)
如图,⊙O的直径 =
=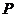 是
是 延长线上的动点,过点
延长线上的动点,过点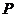 作⊙O的切线,切点为
作⊙O的切线,切点为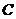 ,连结
,连结 .若
.若 的平分线交
的平分线交 于点
于点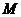 ,你认为∠
,你认为∠ 的大小是否发生变化?若变化,请说明理由;若不变,求出∠
的大小是否发生变化?若变化,请说明理由;若不变,求出∠ 的度数.
的度数.

七、解答题(本题满分7分)
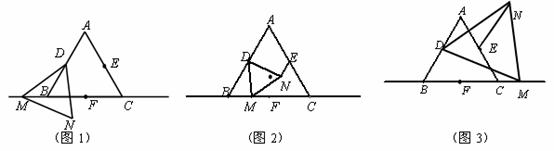
23.如图,已知等边三角形ABC中,点D、E、F分别为边AB、AC、BC的中点,M为直线BC上一动点,△DMN为等边三角形(点M的位置改变时, △DMN也随之整体移动).
(1)如图1,当点M在点B左侧时,请你连结EN,并判断EN与MF有怎样的数量关系?点F是否在直线NE上?请写出结论,并说明理由;
(2)如图2,当点M在BC上时,其它条件不变,(1)的结论中EN与MF的数量关系是否仍然成立? 若成立,请利用图2证明;若不成立,请说明理由;
(3)如图3,若点M在点C右侧时,请你判断(1)的结论中EN与MF的数量关系是否仍然成立? 若成立,请直接写出结论;若不成立,请说明理由.
八、解答题(本题满分7分)
24.对于三个数 ,
,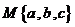 表示
表示 这三个数的平均数,
这三个数的平均数,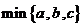 表示
表示 这三个数中最小的数,如:
这三个数中最小的数,如: ,
, ;
;
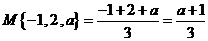 ,
, .
.
解决下列问题:
(1)填空: ;若
;若 ,则
,则 的取值范围是
;
的取值范围是
;
(2)①若 ,那么
,那么 =
;
=
;
②根据①,你发现结论“若 ,那么
”(填
,那么
”(填 大小关系);
大小关系);
③运用②,填空:若
 ,则
,则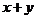 =
;
=
;
(3)在同一直角坐标系中作出函数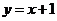 ,
,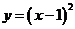 ,
, 的图象(不需列表,描点),通过图象,得出
的图象(不需列表,描点),通过图象,得出 最大值为
.
最大值为
.

九、解答题(本题满分8分)
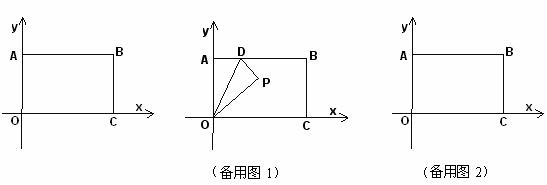
25.如图,矩形OABC的边OC、OA分别与 轴、
轴、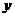 轴重合,点B的坐标是
轴重合,点B的坐标是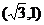 ,点D是AB边上一个动点(与点A不重合),沿OD将△OAD翻折,点A落在点P处.
,点D是AB边上一个动点(与点A不重合),沿OD将△OAD翻折,点A落在点P处.
(1)若点P在一次函数 的图象上,求点P的坐标;
的图象上,求点P的坐标;
(2)若点P在抛物线 图象上,并满足△PCB是等腰三角形,求该抛物线解析式;
图象上,并满足△PCB是等腰三角形,求该抛物线解析式;
(3)当线段OD与PC所在直线垂直时,在PC所在直线上作出一点M,使DM+BM最小,并求出这个最小值.