2009年四川省资阳市高中阶段学校招生统一考试
数学试卷
全卷分为第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分．第Ⅰ卷1至2页，第Ⅱ卷3至8页．全卷满分120分，考试时间共120分钟．
答题前，请考生务必在答题卡上正确填涂自己的姓名、考号和考试科目，并将试卷密封线内的项目填写清楚；考试结束，将试卷和答题卡一并交回．
第Ⅰ卷（选择题 共30分）
注意事项：
每小题选出的答案不能答在试卷上，须用2B铅笔在答题卡上把对应题目的答案标号涂黑．如需改动，用橡皮擦擦净后，再选涂其它答案．
一、选择题：（本大题共10个小题，每小题3分，共30分）在每小题给出的四个选项中，只有一个选项符合题意．
1．?3的绝对值是（ ）
A．3 B．?
2．下列计算正确的是（ ）
A．a+
C．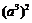
=a9 D．a3÷a4=
（a≠0）
3．吴某打算用同一大小的正多边形地板砖铺设家中的地面，则该地板砖的形状不能是（ ）
A．正三角形 B．正方形 C．正六边形 D．正八边形
4．若一次函数y=kx+b（k≠0）的函数值y随x的增大而增大，则（ ）
A．k<0 B．k>
5．化简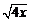
的结果是（ ）
A．2x B．±2x
C．2
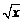D．±2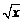
6．在数轴上表示不等式组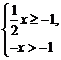
的解集，正确的是（ ）
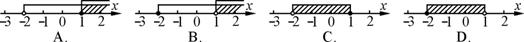7．如图，在矩形ABCD中，若AC=2AB，则∠AOB的大小是（ ）
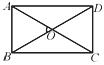
A．30° B．45° C．60° D．90°
8．按下图中第一、二两行图形的平移、轴对称及旋转等变换规律，填入第三行“？”处的图形应是（ ）
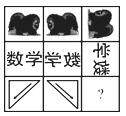
9．用a、b、c、d四把钥匙去开X、Y两把锁，其中仅有a钥匙能够打开X锁，仅有b钥匙能打开Y锁．在求“任意取出一把钥匙能够一次打开其中一把锁”的概率时，以下分析正确的是（ ）
A．分析1、分析2、分析3 B．分析1、分析2
C．分析1 D．分析2
10．如图，已知Rt△ABC的直角边AC=24，斜边AB=25，一个以点P为圆心、半径为1的圆在△ABC内部沿顺时针方向滚动，且运动过程中⊙P一直保持与△ABC的边相切，当点P第一次回到它的初始位置时所经过路径的长度是（ ）
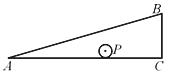
A．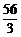
B．25 C．
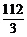D．56
第Ⅱ卷（非选择题 共90分）
二、填空题：（本大题共6个小题,每小题3分,共18分）把答案直接填在题中横线上．
11．甲、乙两人进行跳远训练时，在相同条件下各跳10次的平均成绩相同，若甲的方差为0．3，乙的方差为0．4，则甲、乙两人跳远成绩较为稳定的是_________（填“甲”或“乙”）．
12．方程组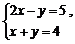
的解是_____________．
13．若两个互补的角的度数之比为1∶2，则这两个角中较小角的度数是_____________．
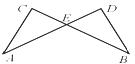
14．如图，已知直线AD、BC交于点E，且AE=BE，欲证明△AEC≌△BED，需增加的条件可以是__________________（只填一个即可）．
15．若点A（?2，a）、B（?1，b）、C（1，c）都在反比例函数y=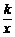
（k<0）的图象上，则用“<”连接a、b、c的大小关系为___________________．
16．若n为整数，且n≤x<n+1，则称n为x的整数部分．通过计算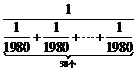
和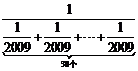
的值，可以确定x=
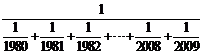的整数部分是______．
三、解答题：（本大题共9个小题，共72分）解答应写出必要的文字说明、证明过程或演算步骤．
17．（本小题满分7分）
解方程：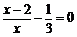
．
18．（本小题满分7分）
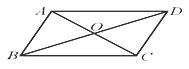
如图，已知□ABCD的对角线AC、BD相交于点O，AC =12，BD=18，且△AOB的周长l=23，求AB的长．
19．（本小题满分8分）
已知Z市某种生活必需品的年需求量y1（万件）、供应量y2（万件）与价格x（元/件）在一定范围内分别近似满足下列函数关系式：y1= ?4x＋190，y2=5x?170．当y1=y2时，称该商品的价格为稳定价格，需求量为稳定需求量；当y1<y2时，称该商品的供求关系为供过于求；当y1>y2时，称该商品的供求关系为供不应求．
（1）（4分） 求该商品的稳定价格和稳定需求量；
（2）（4分） 当价格为45（元/件）时，该商品的供求关系如何？为什么？
20．（小题满分8分）
根据W市统计局公布的数据，可以得到下列统计图表．请利用其中提供的信息回答下列问题：
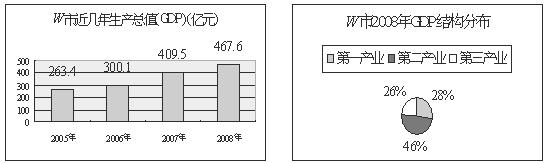
W市近3年人均GDP（元）
年 份
2006年
2007年
2008年
人均GDP
7900
10600
12000
（1）（3分） 从2006年到2008年，W市的GDP哪一年比上一年的增长量最大？
（2）（3分） 2008年W市GDP分布在第三产业的约是多少亿元？（精确到0．1亿元）
（3）（2分） 2008年W市的人口总数约为多少万人？（精确到0．1万人）
21．（本小题满分8分）
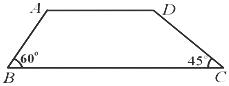
某市在举行“5．12汶川大地震”周年纪念活动时，根据地形搭建了一个台面为梯形（如图所示）的舞台，且台面铺设每平方米售价为a元的木板．已知AB=12米，AD=16米，∠B=60°，∠C=45°，计算购买铺设台面的木板所用资金是多少元．（不计铺设损耗，结果不取近似值）
22．（本小题满分8分）
已知关于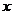
的一元二次方程x2+kx?3=0，
（1）（4分） 求证：不论k为何实数，方程总有两个不相等的实数根；
（2）（4分） 当k=2时，用配方法解此一元二次方程．
23．（本小题满分8分）
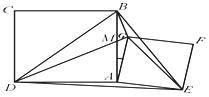
如图，已知四边形ABCD、AEFG均为正方形，∠BAG=α （0°<α<180°）．
（1）（6分） 求证：BE=DG，且 BE⊥DG；
（2）（2分） 设正方形ABCD、AEFG的边长分别是3和2，线段BD、DE、EG、GB所围成封闭图形的面积为S．当α变化时，指出S的最大值及相应的α值．（直接写出结果，不必说明理由）
24．（本小题满分9分）
如图1，已知O是锐角∠XAY的边AX上的动点，以点O为圆心、R为半径的圆与射线AY切于点B，交射线OX于点C．连结BC，作CD⊥BC，交AY于点D．
（1）（3分）求证：△ABC∽△ACD；
（2）（6分）若P是AY上一点，AP=4，且sinA=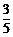
，
① 如图2，当点D与点P重合时，求R的值；
② 当点D与点P不重合时，试求PD的长（用R表示）．
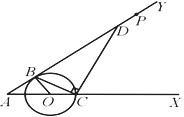
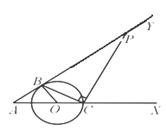
图1 图2
25．（本小题满分9分）
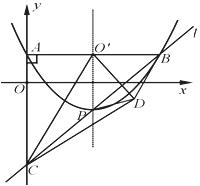
如图，已知抛物线y=
x2?2x＋1的顶点为P，A为抛物线与y轴的交点，过A与y轴垂直的直线与抛物线的另一交点为B，与抛物线对称轴交于点O′，过点B和P的直线l交y轴于点C，连结O′C，将△ACO′沿O′C翻折后，点A落在点D的位置．
（1） （3分） 求直线l的函数解析式；
（2） （3分） 求点D的坐标；
（3） （3分） 抛物线上是否存在点Q，使得S△DQC= S△DPB? 若存在，求出所有符合条件的点Q的坐标；若不存在，请说明理由．
