2009年浙江省初中毕业生学业考试(嘉兴卷)
数学试卷
考生须知:
1.全卷满分150分,考试时间120分钟.试题卷共6页,有三大题,共24小题.
2.全卷答案必须做在答题纸卷Ⅰ、卷Ⅱ的相应位置上,做在试题卷上无效.
参考公式:二次函数
 图象的顶点坐标是
图象的顶点坐标是 .
.
温馨提示:请仔细审题,细心答题,答题前仔细阅读答题纸上的“注意事项”.
卷Ⅰ(选择题)
一、选择题(本题有10小题,每题4分,共40分.请选出各题中唯一的正确选项,不选、多选、错选,均不得分)
1.实数x,y在数轴上的位置如图所示,则( )

A.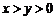 B.
B.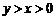 C.
C.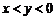 D.
D.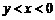
2.若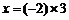 ,则x的倒数是( )
,则x的倒数是( )
A.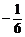 B.
B.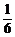 C.
C.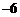 D.6
D.6
3.下列运算正确的是( )
A.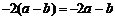 B.
B.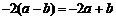
C.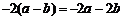 D.
D.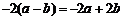
4.已知数据:2,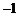 ,3,5,6,5,则这组数据的众数和极差分别是( )
,3,5,6,5,则这组数据的众数和极差分别是( )
A.5和7 B.6和
5.判断下列两个结论:①正三角形是轴对称图形;②正三角形是中心对称图形,结果是( )
A.①②都正确 B.①②都错误
C.①正确,②错误 D.①错误,②正确
6.解方程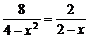 的结果是( )
的结果是( )
A.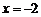 B.
B.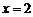 C.
C.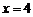 D.无解
D.无解
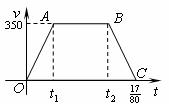
7.沪杭高速铁路已开工建设,某校研究性学习以此为课题,在研究列车的行驶速度时,得到一个数学问题.如图,若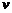 是关于
是关于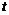 的函数,图象为折线
的函数,图象为折线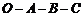 ,其中
,其中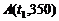 ,
,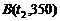 ,
,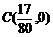 ,四边形
,四边形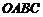 的面积为70,则
的面积为70,则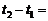 ( )
( )
A.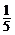 B.
B.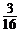 C.
C.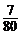 D.
D.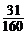
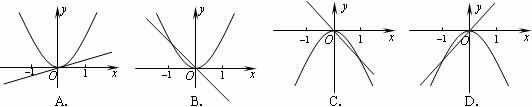
8.已知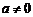 ,在同一直角坐标系中,函数
,在同一直角坐标系中,函数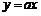 与
与 的图象有可能是( )
的图象有可能是( )
9.如图,⊙P内含于⊙ ,⊙
,⊙ 的弦
的弦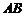 切⊙P于点
切⊙P于点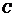 ,且
,且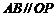 .若阴影部分的面积为
.若阴影部分的面积为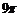 ,则弦
,则弦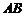 的长为( )
的长为( )

A.3 B.4 C.6 D.9
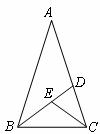
10.如图,等腰△ABC中,底边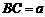 ,
,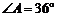 ,
,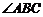 的平分线交AC于D,
的平分线交AC于D,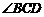 的平分线交BD于E,设
的平分线交BD于E,设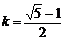 ,则
,则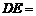 ( )
( )
A.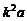 B.
B.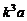 C.
C.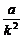 D.
D.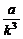
卷Ⅱ(非选择题)
二、填空题(本题有6小题,每题5分,共30分)
11.用四舍五入法,精确到0.1,对5.649取近似值的结果是 .
12.当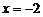 时,代数式
时,代数式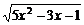 的值是 .
的值是 .
13.因式分解: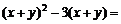 .
.
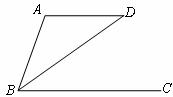
14.如图,AD∥BC,BD平分∠ABC,且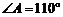 ,则
,则 .
.
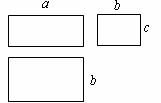
15.一个几何体的三视图如图所示(其中标注的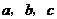 为相应的边长),则这个几何体的体积是 .
为相应的边长),则这个几何体的体积是 .
16.如图,在直角坐标系中,已知点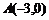 ,
,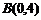 ,对△
,对△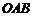 连续作旋转变换,依次得到三角形①、②、③、④…,则三角形⑩的直角顶点的坐标为 .
连续作旋转变换,依次得到三角形①、②、③、④…,则三角形⑩的直角顶点的坐标为 .
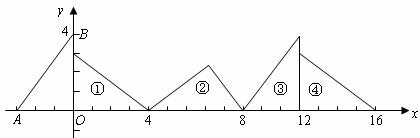
三、解答题(本题有8小题,第17~20题每题8分,第21题10分,第22、23题每题12分,第24题14分,共80分)
17.计算: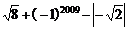 .
.
18.化简: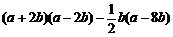 .
.
19.在四边形ABCD中,∠D=60°,∠B比∠A大20°,∠C是∠A的2倍,求∠A,∠B,∠C的大小.
20.某工厂用A、B、C三台机器加工生产一种产品。对2009年第一季度的生产情况进行统计,图1是三台机器的产量统计图,图2是三台机器产量的比例分布图.(图中有部分信息未给出)
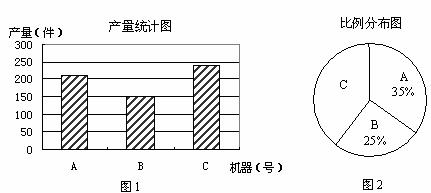
(1)利用图1信息,写出B机器的产量,并估计A机器的产量;
(2)综合图1和图2信息,求C机器的产量.
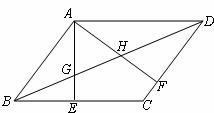
21.如图,在平行四边形ABCD中,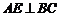 于E,
于E,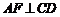 于F,BD与AE、AF分别相交于G、H.
于F,BD与AE、AF分别相交于G、H.
(1)求证:△ABE∽△ADF;
(2)若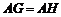 ,求证:四边形ABCD是菱形.
,求证:四边形ABCD是菱形.
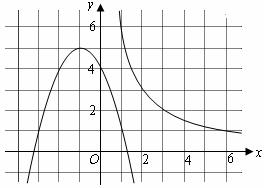
22.如图,曲线C是函数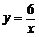 在第一象限内的图象,抛物线是函数
在第一象限内的图象,抛物线是函数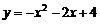 的图象.点
的图象.点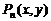 (
(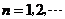 )在曲线C上,且
)在曲线C上,且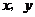 都是整数.
都是整数.
(1)求出所有的点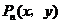 ;
;
(2)在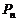 中任取两点作直线,求所有不同直线的条数;
中任取两点作直线,求所有不同直线的条数;
(3)从(2)的所有直线中任取一条直线,求所取直线与抛物线有公共点的概率.
23.如图,已知一次函数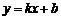 的图象经过
的图象经过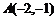 ,
,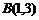 两点,并且交x轴于点C,交y轴于点D,
两点,并且交x轴于点C,交y轴于点D,
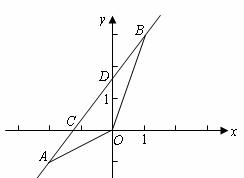
(1)求该一次函数的解析式;
(2)求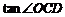 的值;
的值;
(3)求证: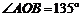 .
.
24.如图,已知A、B是线段MN上的两点,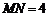 ,
,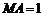 ,
,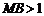 .以A为中心顺时针旋转点M,以B为中心逆时针旋转点N,使M、N两点重合成一点C,构成△ABC,设
.以A为中心顺时针旋转点M,以B为中心逆时针旋转点N,使M、N两点重合成一点C,构成△ABC,设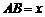 .
.
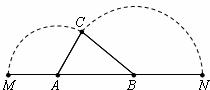
(1)求x的取值范围;
(2)若△ABC为直角三角形,求x的值;
(3)探究:△ABC的最大面积?
2009年浙江省初中毕业生学业考试(嘉兴卷)
一、选择题(本题有10小题,每题4分,共40分)
1.B 2.A 3.D 4.A 5.C
6.D 7.B 8.C 9.C 10.A
二、填空题(本题有6小题,每题5分,共30分)
11.5.6 12.5
13. 14.
14.
15. 16.
16.
三、解答题(本题有8小题,第17~20题每题8分,第21题10分,第22、23题每题12分,第24题14分,共80分)
17.
 ????????????????????????????????????????????????????????????????????????????????????????????????? 6分
????????????????????????????????????????????????????????????????????????????????????????????????? 6分
 ?????????????????????????????????????????????????????????????????????????????????????????????????? 8分
?????????????????????????????????????????????????????????????????????????????????????????????????? 8分
18.
 ??????????????????????????????????????????????????????????????????????????????????? 6分
??????????????????????????????????????????????????????????????????????????????????? 6分
 ????????????????????????????????????????????????????????????????????????????????????????????????????? 8分
????????????????????????????????????????????????????????????????????????????????????????????????????? 8分
19.设 (度),则
(度),则 ,
, .
.
根据四边形内角和定理得, . ???????????????????????????????????? 4分
. ???????????????????????????????????? 4分
解得, .
.
∴ ,
, ,
, . ???????????????????????????????????????????????????????????????? 8分
. ???????????????????????????????????????????????????????????????? 8分
20.(1)B机器的产量为150件, ???????????????????????????????????????????????????????????????????????????? 2分
A机器的产量约为210件. ???????????????????????????????????????????????????????????????????????? 4分
(2)C机器产量的百分比为40%. ?????????????????????????????????????????????????????????????????????? 6分
设C机器的产量为x,
由 ,得
,得 ,即C机器的产量为240件. ???????????????????????????????? 8分
,即C机器的产量为240件. ???????????????????????????????? 8分
21.

(1)∵AE⊥BC,AF⊥CD,∴∠AEB=∠AFD=90°. ??????????????????????????????????????????????? 2分
∵四边形ABCD是平行四边形,∴∠ABE=∠ADF. ?????????????????????????????????????? 4分
∴△ABE∽△ADF ??????????????????????????????????????????????????????????????????????????????????? 5分
(2)∵△ABE∽△ADF,
∴∠BAG=∠DAH.
∵AG=AH,∴∠AGH=∠AHG,
从而∠AGB=∠AHD.
∴△ABG≌△ADH. ????????????????????????????????????????????????????????????????????????????????????????? 8分
∴ .
.
∵四边形ABCD是平行四边形,
∴四边形ABCD是菱形. ?????????????????????????????????????????????????????????????????? 10分
22.(1)∵ 都是正整数,且
都是正整数,且 ,∴
,∴ .
.
∴ ,
, ,
, ,
, ??????????????????????????????????????????????????????????????? 4分
??????????????????????????????????????????????????????????????? 4分
(2)从 ,
, ,
, ,
, 中任取两点作直线为:
中任取两点作直线为:
 ,
, ,
, ,
, ,
, ,
, .
.
∴不同的直线共有6条. ??????????????????????????????????????????????????????????????????????????????????? 9分
(3)∵只有直线 ,
, 与抛物线有公共点,
与抛物线有公共点,
∴从(2)的所有直线中任取一条直线与抛物线有公共点的概率是 ?????????? 12分
?????????? 12分
23.(1)由 ,解得
,解得 ,所以
,所以 ?????????????????????????????????????????? 4分
?????????????????????????????????????????? 4分
(2) ,
, .
.
在 △OCD中,
△OCD中, ,
, ,
,
∴
 . ???????????????????????????????????????????????????????????????????????????????? 8分
. ???????????????????????????????????????????????????????????????????????????????? 8分
(3)取点A关于原点的对称点 ,则问题转化为求证
,则问题转化为求证 .
.

由勾股定理可得,
 ,
, ,
, ,
,
∵ ,
,
∴△EOB是等腰直角三角形.
∴ .
.
∴ .??????????????????????????????????????????????????????????????????????????????????????????? 12分
.??????????????????????????????????????????????????????????????????????????????????????????? 12分
24.(1)在△ABC中,∵ ,
, ,
, .
.
∴ ,解得
,解得 . ????????????????????????????????????????????????????????????????? 4分
. ????????????????????????????????????????????????????????????????? 4分
(2)①若AC为斜边,则 ,即
,即 ,无解.
,无解.
②若AB为斜边,则 ,解得
,解得 ,满足
,满足 .
.
③若BC为斜边,则 ,解得
,解得 ,满足
,满足 .
.
∴ 或
或 . ??????????????????????????????????????????????????????????????????????????????????????????? 9分
. ??????????????????????????????????????????????????????????????????????????????????????????? 9分
(3)在△ABC中,作 于D,设
于D,设 ,△ABC的面积为S,则
,△ABC的面积为S,则 .
.

①若点D在线段AB上,则 .
.
∴ ,即
,即 .
.
∴ ,即
,即 .
.
∴
 (
( ). ?????????????????? 11分
). ?????????????????? 11分
当 时(满足
时(满足 ),
), 取最大值
取最大值 ,从而S取最大值
,从而S取最大值 .?????????? 13分
.?????????? 13分
②若点D在线段MA上,则 .
.

同理可得,
 (
( ),
),
易知此时 .
.
综合①②得,△ABC的最大面积为 ???????????????????????????????????????????????????????????? 14分
???????????????????????????????????????????????????????????? 14分